„Mintázat 2.óra” változatai közötti eltérés
(→Árnyékleképezés (shadowgraph)) |
(→Árnyékleképezés (shadowgraph)) |
||
| 22. sor: | 22. sor: | ||
A fenti, balról a második ábrán látható gradiens indexű lencse (gradient index lens) éppen úgy fókuszálja (vagy defókuszálja) a fényt, ahogy az árnyékleképezés során az inhomogén anyagok keresztülhaladó fénnyel is történik. A lencse működését a fenti ábra jól szemlélteti. Egy egyszerű, (például) kocka alakú tárgyról van szó, melynek törésmutatója inhomogén és így a domború lencsékhez hasonlóan fókuszálja a fényt. | A fenti, balról a második ábrán látható gradiens indexű lencse (gradient index lens) éppen úgy fókuszálja (vagy defókuszálja) a fényt, ahogy az árnyékleképezés során az inhomogén anyagok keresztülhaladó fénnyel is történik. A lencse működését a fenti ábra jól szemlélteti. Egy egyszerű, (például) kocka alakú tárgyról van szó, melynek törésmutatója inhomogén és így a domború lencsékhez hasonlóan fókuszálja a fényt. | ||
| + | |||
| + | ===Példa: Rayleigh-Bénard áramlás vizualizálása=== | ||
| + | Az árnyékleképezés bemutatására jó példa az alulról fűtött folyadékban (pl. szilikonolaj) kialakuló Rayleigh-Bénard áramlás. Ha elég nagy a függőleges hőmérséklet-gradiens (a pontos képletet egy későbbi órán), folyadékáramlás indul meg. Az alul lévő melegebb (emiatt kisebb sűrűségű) anyag fölfelé, míg a fölül lévő hidegebb (emiatt nagyobb sűrűségű) anyag lefelé igyekszik. Így kialakulhat egy körkörös föl- és leáramlás. | ||
| + | |||
| + | <gallery widths=200px heights=200px caption="A Rayleigh-Bénard áramlás vizualizálása árnyékleképezéssel"> | ||
| + | Image:rayleigh-bénard-oldalról.png|Az áramlás oldalnézetből | ||
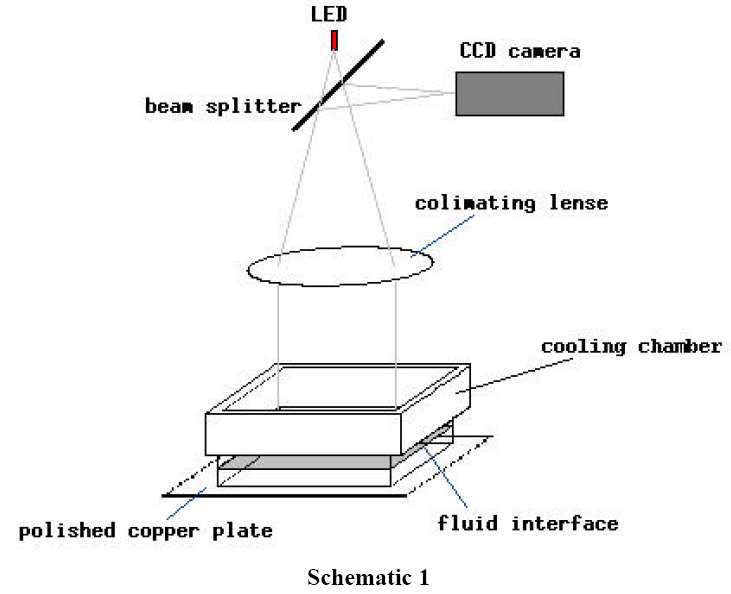
| + | Image:shadowgraph-rayleigh-bénard.png|A berendezés vázlatos képe | ||
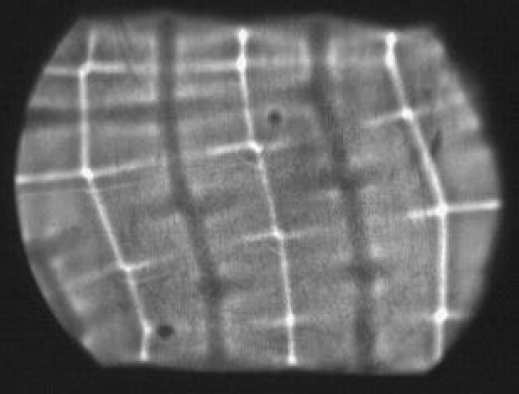
| + | Image:rayleigh-bénard-felülről-fotó.png|Az áramlás árnyékképe felülről, 1 cm vastag olajréteg esetén, 1<sup>o</sup>C-os hőmérsékletkülönbségnél. | ||
| + | </gallery> | ||
| + | |||
| + | ===Árnyékleképezés napfénnyel=== | ||
| + | A Nap, mint fényforrás előnyei, hogy intenzív és nagyon nagy objektumokra is alkalmazható. Hátránya, hogy nem pontszerű, emiatt a keletkező kép széle elmosódott lesz. A felbontási küszöböt az alábbi vázlatos ábra alapján a következő egyenletekkel becsüljük. | ||
| + | |||
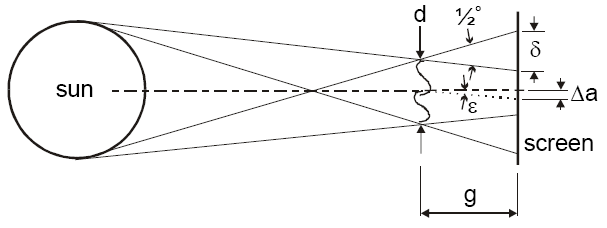
| + | [[Image:nap-fényforrás.png|center|thumb|400px|A Nap, mint fényforrás alkalmazása során a felbontási küszöb becslése]] | ||
| + | |||
| + | <p align="center"><math>\frac{\delta}{g} = tan \left( \frac{1}{2}^o \right) = 0,009</math><br> | ||
| + | <math>\Delta a = g \cdot tan \epsilon</math><br> | ||
| + | <math>\frac{\Delta a}{\delta} = \frac{tan \epsilon}{\tan \left( \frac{1}{2}^o \right)} \approx \frac{\epsilon}{\frac{1}{2}^o}</math><br></p> | ||
| + | |||
| + | A fenti képletekből látható, hogy túl nagy, vagy túl kicsi relatív ernyőtávolság <math>\left( \frac{g}{d} \right)</math> esetén nem lesz jó a kép. Az optimális távolság: <math>20 \le \frac{g}{d} \le 30</math> között van. | ||
==Schlieren technika== | ==Schlieren technika== | ||
A lap 2011. december 17., 13:34-kori változata
Az alábbi órán a különböző kísérleti technikák működési elvével foglalkoztunk. Fontos tudni, hogy a jelen órán vizsgált rendszereknél a válasz nem lineáris a perturbációval, azaz ha van két megoldásunk, akkor ezek lineárkombinációja nem lesz megoldás. A továbbiakban ezen az órán olyan technikákkal fogunk foglalkozni, amelyek segítségével a kis amplitudójú, vagy bonyolult geometriájú esetben a térbeli struktúrákat láthatóvá lehet tenni.
Tartalomjegyzék
- 1 Kísérleti technikák
- 2 Árnyékleképezés (shadowgraph)
- 3 Schlieren technika
- 4 Polarizációs mikroszkópia (kettőstörés)
- 5 Fáziskontraszt mikroszkópia
- 6 Interferencia mikroszkópia
- 7 Periodikus struktúrák detektálása diffrakcióval (helyérzékeny fotodetektorok)
- 8 Sebességmérés áramlásokban (Particle Image Velocity - PIV)
- 9 Sebességmérés áramlásokban (Particle Tracking)
- 10 Nem átlászó rendszerek belsejében lejátszódó jelenségek vizualizálása (index matching)
- 11 Nem átlászó rendszerek belsejében lejátszódó jelenségek vizualizálása (PEPT, DWS, MRI, CT)
- 12 CCD és CMOS szenzorok tulajdonságai
- 13 Hivatkozások
Kísérleti technikák
A következő technikákkal foglalkozunk az alábbiakban:
- Árnyékleképezés (shadowgraph), schlieren technika
- Polarizációs mikroszkópia (kettőstörés), fáziskontraszt és interferencia mikroszkópia
- Periodikus struktúrák detektálása diffrakcióval (helyérzékeny fotodetektorok)
- Sebességmérés áramlásokban (Particle Image Velocimetry - PIV, Particle Tracking)
- Nem átlátszó rendszerek belsejében lejátszódó jelenségek vizualizálása (index matching, PEPT, DWS, MRI, CT)
- CCD és CMOS szenzorok tulajdonságai
Árnyékleképezés (shadowgraph)
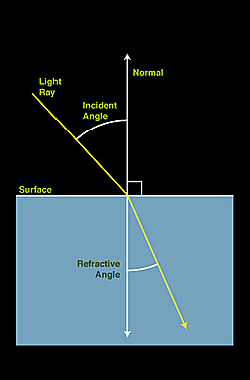
Lényege: intenzív, monokromatikus fényforrással optikai inhomogenitások árnyékképét hozzuk létre. A jelenség alapja, hogy a fény az optikailag sűrűbb közeg felé törik (hajlik el - lásd lentebb a bal oldali ábrát). Egy inhomogén optikai közeg (például egy gyertyaláng) különböző részei fókuszálják, más részei pedig defókuszálják a beérkező fénynyalábot, így kialakul egy árnyékkép. Az árnyékkép alakjából pedig következtetni tudunk a megfigyelt minta sűrűségeloszlására. Természetesen ez a technika csak optikailag átlátszó közegek esetén (pl. levegő, víz, üveg) alkalmazható.
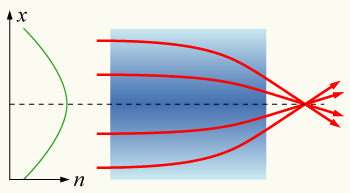
A fenti, balról a második ábrán látható gradiens indexű lencse (gradient index lens) éppen úgy fókuszálja (vagy defókuszálja) a fényt, ahogy az árnyékleképezés során az inhomogén anyagok keresztülhaladó fénnyel is történik. A lencse működését a fenti ábra jól szemlélteti. Egy egyszerű, (például) kocka alakú tárgyról van szó, melynek törésmutatója inhomogén és így a domború lencsékhez hasonlóan fókuszálja a fényt.
Példa: Rayleigh-Bénard áramlás vizualizálása
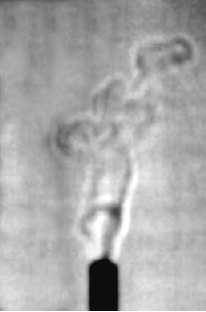
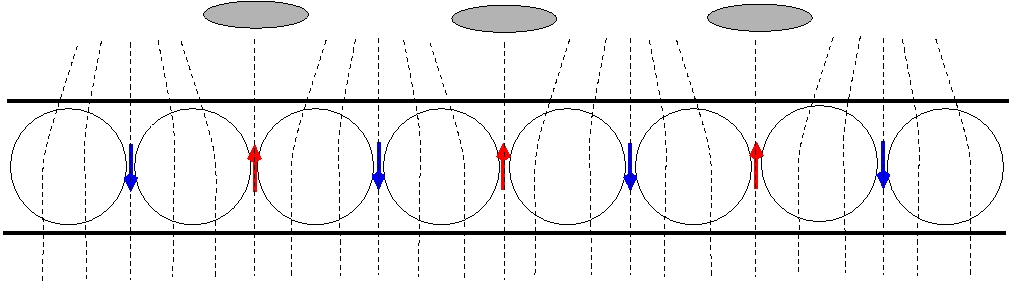
Az árnyékleképezés bemutatására jó példa az alulról fűtött folyadékban (pl. szilikonolaj) kialakuló Rayleigh-Bénard áramlás. Ha elég nagy a függőleges hőmérséklet-gradiens (a pontos képletet egy későbbi órán), folyadékáramlás indul meg. Az alul lévő melegebb (emiatt kisebb sűrűségű) anyag fölfelé, míg a fölül lévő hidegebb (emiatt nagyobb sűrűségű) anyag lefelé igyekszik. Így kialakulhat egy körkörös föl- és leáramlás.
- A Rayleigh-Bénard áramlás vizualizálása árnyékleképezéssel
Árnyékleképezés napfénnyel
A Nap, mint fényforrás előnyei, hogy intenzív és nagyon nagy objektumokra is alkalmazható. Hátránya, hogy nem pontszerű, emiatt a keletkező kép széle elmosódott lesz. A felbontási küszöböt az alábbi vázlatos ábra alapján a következő egyenletekkel becsüljük.
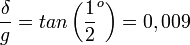
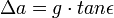
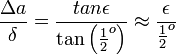
A fenti képletekből látható, hogy túl nagy, vagy túl kicsi relatív ernyőtávolság  esetén nem lesz jó a kép. Az optimális távolság:
esetén nem lesz jó a kép. Az optimális távolság: 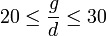 között van.
között van.