Szilárdtestfizika

Neumann-elv:kristályos anyag bármilyen mérhető fizikai mennyiségének szimmetriatulajdonságait vizsgálva a szimmetriák között jelen kell lennie a kristály pontcsoportja minden szimmetriaelemének.

Irányfüggő fizikai tulajdonságokra vonatkoztatva így is megfogalmazhatjuk: egy kristály bármely irányfüggő makroszkopikus fizikai tulajdonsága invariáns a kristályosztály szimmetriaműveleteivel szemben.

Wigner-tétel (szavakban megfogalmazva): ha 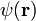$\psi (\mathbf{r})$ a Hamilton-operátor sajátfüggvénye $\epsilon$ energia-sajátértékkel, akkor a Hamilton-operátort invariánsan hagyó, azal felcserélhető T(G_i) szimmetriaművelettel előállított 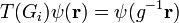$T(G_i)\psi(\mathbf{r}) = \psi(g^{-1}\mathbf{r})$ is sajátfüggvény ugyanazzal az energiával.