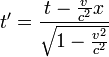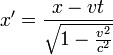„Lorentz transzformáció” változatai közötti eltérés
(Új oldal, tartalma: „ :<math>t'=\frac{t - \frac{v}{c^{2}}x}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} \qquad</math> :<math>x'=\frac{x - vt}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} \qquad</math><br /><br /> …”) |
Naxa (vitalap | szerkesztései) |
||
| (2 közbenső módosítás, amit 2 másik szerkesztő végzett, nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| − | |||
| − | |||
:<math>t'=\frac{t - \frac{v}{c^{2}}x}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} \qquad</math> | :<math>t'=\frac{t - \frac{v}{c^{2}}x}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} \qquad</math> | ||
| − | :<math>x'=\frac{x - vt}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} \qquad</math><br /><br /> | + | :<math>x'=\frac{x - vt}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} \qquad</math> |
| − | + | <noinclude> | |
| + | <br /><br /> | ||
| 12. sor: | 11. sor: | ||
| − | Bővebben: [[]] | + | Bővebben: [[A relativitás elmélet alapjai#A Lorentz-transzformáció]] |
| + | </noinclude> | ||