„Mintázat 2.óra” változatai közötti eltérés

Innen: TételWiki
(→‎Árnyékleképezés (shadowgraph))
a (→‎Hivatkozások)
 
(10 közbenső módosítás ugyanattól a szerkesztőtől nincs mutatva)
14. sor: 14. sor:
 
Lényege: intenzív, monokromatikus fényforrással optikai inhomogenitások árnyékképét hozzuk létre. A jelenség alapja, hogy a fény az optikailag sűrűbb közeg felé törik (hajlik el - lásd lentebb a bal oldali ábrát). Egy inhomogén optikai közeg (például egy gyertyaláng) különböző részei fókuszálják, más részei pedig defókuszálják a beérkező fénynyalábot, így kialakul egy árnyékkép. Az árnyékkép alakjából pedig következtetni tudunk a megfigyelt minta sűrűségeloszlására. Természetesen ez a technika csak optikailag átlátszó közegek esetén (pl. levegő, víz, üveg) alkalmazható.
 
Lényege: intenzív, monokromatikus fényforrással optikai inhomogenitások árnyékképét hozzuk létre. A jelenség alapja, hogy a fény az optikailag sűrűbb közeg felé törik (hajlik el - lásd lentebb a bal oldali ábrát). Egy inhomogén optikai közeg (például egy gyertyaláng) különböző részei fókuszálják, más részei pedig defókuszálják a beérkező fénynyalábot, így kialakul egy árnyékkép. Az árnyékkép alakjából pedig következtetni tudunk a megfigyelt minta sűrűségeloszlására. Természetesen ez a technika csak optikailag átlátszó közegek esetén (pl. levegő, víz, üveg) alkalmazható.
  
−
[[Kép:refraction.png|thumb|none|400px|A fénytörés jelensége]]
+
<gallery widths=200px heights=200px>
−
[[Kép:gradient_index_lens.png|thumb|center|400px|Gradiens indexű lencse fényfókuszálása]]
+
Image:refraction.png|A fénytörés jelensége
 +
Image:gradient_index_lens.png|Gradiens indexű lencse fényfókuszálása
 +
Image:refraction_car.png|Az autó fölött "fodrozódó" levegő is a fent ismertetett hatás következménye
 +
Image:gyertyaláng-shadowgraph.png|A gyertyaláng árnyékképe
 +
</gallery>
 +
 
 +
A fenti, balról a második ábrán látható gradiens indexű lencse (gradient index lens) éppen úgy fókuszálja (vagy defókuszálja) a fényt, ahogy az árnyékleképezés során az inhomogén anyagok keresztülhaladó fénnyel is történik. A lencse működését a fenti ábra jól szemlélteti. Egy egyszerű, (például) kocka alakú tárgyról van szó, melynek törésmutatója inhomogén és így a domború lencsékhez hasonlóan fókuszálja a fényt.
 +
 
 +
===Példa: Rayleigh-Bénard áramlás vizualizálása===
 +
Az árnyékleképezés bemutatására jó példa az alulról fűtött folyadékban (pl. szilikonolaj) kialakuló Rayleigh-Bénard áramlás. Ha elég nagy a függőleges hőmérséklet-gradiens (a pontos képletet egy későbbi órán), folyadékáramlás indul meg. Az alul lévő melegebb (emiatt kisebb sűrűségű) anyag fölfelé, míg a fölül lévő hidegebb (emiatt nagyobb sűrűségű) anyag lefelé igyekszik. Így kialakulhat egy körkörös föl- és leáramlás.
 +
 
 +
<gallery widths=200px heights=200px caption="A Rayleigh-Bénard áramlás vizualizálása árnyékleképezéssel">
 +
Image:rayleigh-bénard-oldalról.png|Az áramlás oldalnézetből
 +
Image:shadowgraph-rayleigh-bénard.png|A berendezés vázlatos képe
 +
Image:rayleigh-bénard-felülről-fotó.png|Az áramlás árnyékképe felülről, 1 cm vastag olajréteg esetén, 1<sup>o</sup>C-os hőmérsékletkülönbségnél.
 +
</gallery>
 +
 
 +
===Árnyékleképezés napfénnyel===
 +
A Nap, mint fényforrás előnyei, hogy intenzív és nagyon nagy objektumokra is alkalmazható. Hátránya, hogy nem pontszerű, emiatt a keletkező kép széle elmosódott lesz. A felbontási küszöböt az alábbi vázlatos ábra alapján a következő egyenletekkel becsüljük.
 +
 
 +
[[Image:nap-fényforrás.png|center|thumb|400px|A Nap, mint fényforrás alkalmazása során a felbontási küszöb becslése]]
 +
 
 +
<p align="center"><math>\frac{\delta}{g} = tan \left( \frac{1}{2}^o \right) = 0,009</math><br>
 +
<math>\Delta a = g \cdot tan \epsilon</math><br>
 +
<math>\frac{\Delta a}{\delta} = \frac{tan \epsilon}{\tan \left( \frac{1}{2}^o \right)} \approx \frac{\epsilon}{\frac{1}{2}^o}</math><br></p>
 +
 
 +
A fenti képletekből látható, hogy túl nagy, vagy túl kicsi relatív ernyőtávolság <math>\left( \frac{g}{d} \right)</math> esetén nem lesz jó a kép. Az optimális távolság: <math>20 \le \frac{g}{d} \le 30</math> között van.
  
 
==Schlieren technika==
 
==Schlieren technika==
 +
[[Image:schlieren-technika.png|center|thumb|400px|A Schliere-technikával működő berendezés vázlatos képe]]
 +
 +
A Schlieren-technika segítségével optikailag átlátszó anyagban vizsgálhatunk kis sűrűség-inhomogenitásokat. A technika lényege, hogy az "A" helyen lévő kis sűrűség-inhomogenitást úgy jelenítjük meg, hogy a párhuzamos nyalábot összefókuszáló lencse gyújtópontjába egy pengét tolunk. Ha az "A" helyen lévő közeg teljesen homogén, akkor a kép hirtelen tűnik el, amikor a penge a fókuszpontba ér. Ha azonban az "A" helyen lévő közeg inhomogén, akkor a penge betolásával az ernyőn folytonosan változik a kép, és a direkt nyalábot kitakarva az inhomogenitás jól láthatóvá válik.
 +
 +
<gallery widths=400px heights=190px caption="Néhány példa a Shlieren-technikával történő ábrázolásra">
 +
Image:schlieren-pohár.png|Borospohár körül áramló gáz képe
 +
Image:schlieren-ember.png|Az emberi lehellet képe
 +
</gallery>
 +
 +
===Plazmabuborék határán fellépő Richtmyer-Meshkov instabilitás vizualizálása Schlieren-technikával===
 +
Egy függőleges cső aljában parabolatükröt helyeznek el. A fölülről érkező nyalábot a tükör fókuszálja, ennek következtében a csőben lévő gázban egy plazmabuborék jön létre (az alábbi, jobb oldali képen fehér tartomány). A buborék keletkezésekor egy lökéshullám indul meg gömb alakban kifelé, mely a parabolatükörről visszaverődve párhuzamos hullámfrontként halad előre, majd nekiütközik magának a buboréknak, aminek határa a lökéshullámmal való kölcsönhatás következtében instabillá válik (112 <math>\mu s</math>): kialakul az úgynevezett Richtmyer-Meshkov instabilitás (mely a Rayleigh-Taylor instabilitás egy formája, mindkettőről szó lesz a 4. órán).
 +
 +
<gallery widths=200px heights=200px caption="A Richtmyer-Meshkov instabilitás vizualizálása Schlieren-technikával">
 +
Image:schlieren-plazmabuborék-berendezés.png|A berendezés vázlatos képe
 +
Image:schlieren-plazmabuborék-képek.png|A plazmabuborékról készült képek
 +
</gallery>
  
 
==Polarizációs mikroszkópia (kettőstörés)==
 
==Polarizációs mikroszkópia (kettőstörés)==
 +
Bizonyos kristályokban a lineárisan poláros fény sebessége függ attól, hogy melyik kristálytengely irányában halad. Ennek oka az, hogy az anyag anizotróp, és különböző mértékben polarizálható a különböző irányokban.
 +
 +
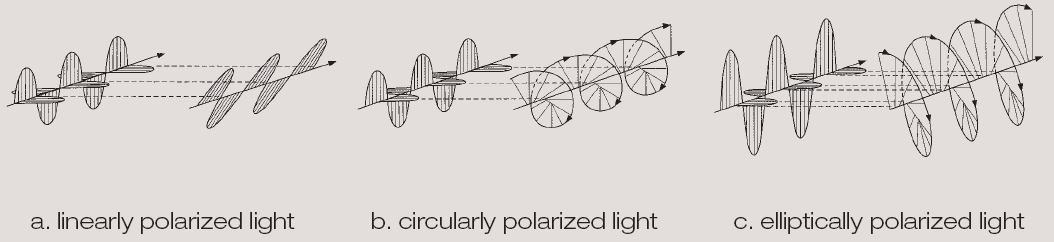
[[Image:polarizációk.png|center|thumb|400px|A különböző polarizációk szemléltetése]]
 +
 +
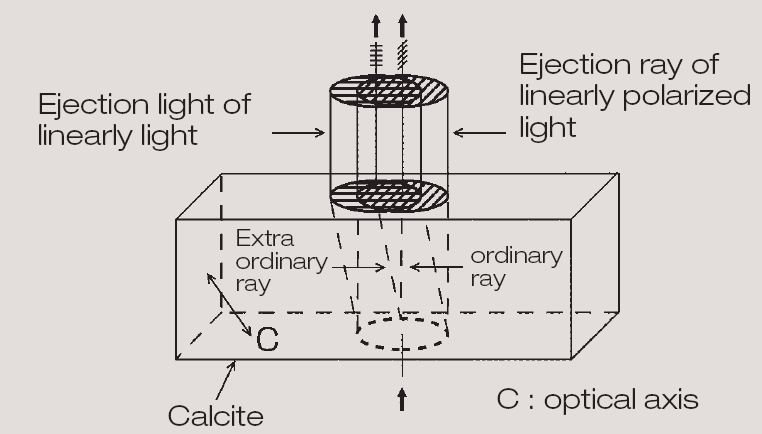
'''Kettőstörés:''' A (kettőstörő) kristályba belépő fény két sugárra bomlik, amelyek közül az egyik, az úgynevezett rendes vagy ordinárius sugár szabály szerint követi a törés törvényét, a másik, a rendellenes vagy extraordinárius sugár azonban nem. Így törik meg a rendes sugár és a rendellenes sugár a kettős töréskor.
 +
 +
A jelenség azzal magyarázható, hogy míg a rendes (ordinárius - o) sugár esetén a hullámfront pontjaiból rendes kör- (gömb)hullámok indulnak ki, a rendellenes (extraordinárius - e) sugár esetén ezek az elemi hullámok ellipszis alakot vesznek fel, aminek az az oka, hogy a kristály szerkezete miatt a kristályban az adott irányban megváltozik a fény terjedési sebessége. A rendellenes (eo) sugár esetén a törésmutató a beeső sugár irányától is függ, és (a törés törvényével szemben) a megtört sugár általában nem marad a beesési síkban.
 +
 +
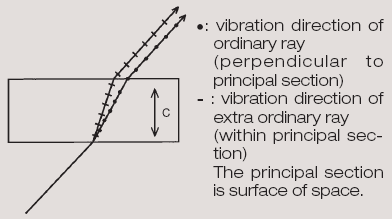
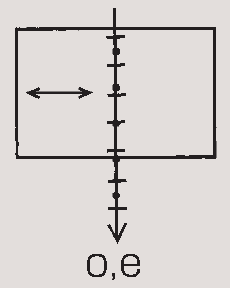
Egytengelyű kristályokban általános esetben az optikai tengely és a nyaláb iránya jelöli ki az ordinárius és extraordinárius nyalábok vibrációs irányát. A mteszetet, ami mindkét nyalábot tartalmazza, fősíknak (principal section) nevezzük. Az ordinárius nyalábban a tér a fősíkra merőlegesen, míg az extraordinárius nyalábban a fősíkban oszcillál.
 +
 +
A törésmutató anizotrópia az extraordinárius (az optikai tengellyel párhuzamos polarizációjú) és az ordinárius (a tengelyre merőleges polarizációjú) nyalábokra vonatkozó törésmutatók különbsége: <math>\Delta n = n_e - n_o</math>
 +
 +
<gallery widths=200px heights=100px caption="A kettőstörést szemléltető ábrák">
 +
Image:kettőstörés.png|Az ordinárius és extraordinárius nyalábok szemléltetése
 +
Image:kettőstörés_fősík.png|A fősík szemléltetése
 +
Image:kettőstörés_kalcit.png|Kettőstörés kalcitban
 +
Image:kettőstörés_példa.png|Vizuális példa a kettőstörésre
 +
</gallery>
 +
 +
A kettőstörő anyag a két nyaláb (o és e) fázisát eltolja egymáshoz képest. Így a bejövő lineárisan poláros fény a mintát elhagyva általában elliptikusan poláros lesz. Ez a jelenség a kettőstörő anyagokban jól használható orientációs inhomogenitások vizsgálatára és azok időbeli változásának nyomon követésére - méghozzá polarizátorokkal felszerelt mikroszkóp segítségével.
 +
 +
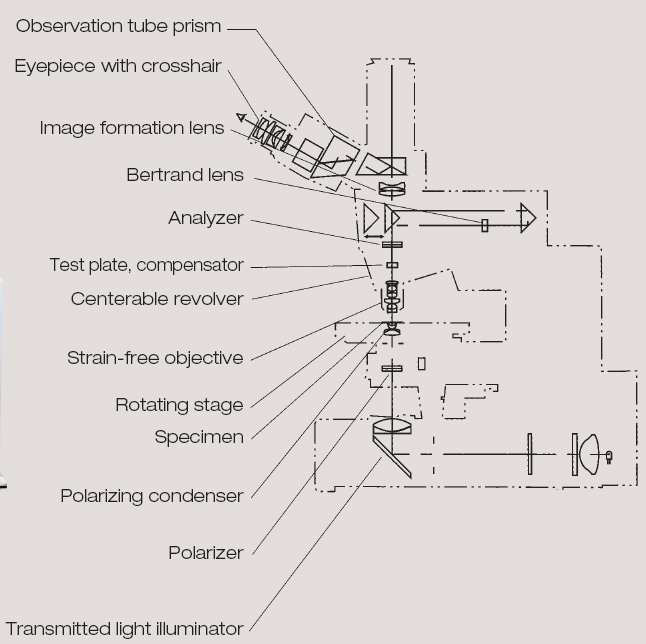
[[Image:polarizációs_mikroszkóp_vázlat.png|center|thumb|400px|A polarizációs mikroszkóp vázlatos felépítése]]
 +
 +
A mikroszkópba vékony <math>\left( \sim 10 \mu m \right)</math> szeletet téve a különböző orientációjú domének különböző mértékeben tolják el a két (o és e) nyaláb fázisát, így különböző színük (illetve monokromatikus fény esetén különböző intenzitásuk) lesz.
 +
 +
Megfelelően polarizált nyalábot használva a kettőstörő anyag árnyékleképezése optimalizálható.
 +
 +
<gallery widths=330px heights=200px caption="Példák a polarizációs mikroszkóppal készült felvételekre">
 +
Image:vitamin_kristály.png|Vitamin kristály
 +
Image:folyadékkristály.png|A folyadékkristály optikai mintázatai
 +
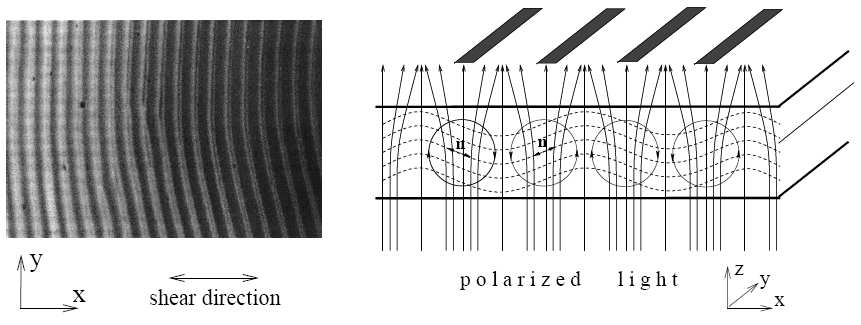
Image:foly_krist_nyírás.png|Nematikus folyadékkristályban nyírás hatására kialakult hengeres áramlás képe
 +
</gallery>
  
 
==Fáziskontraszt mikroszkópia==
 
==Fáziskontraszt mikroszkópia==
 +
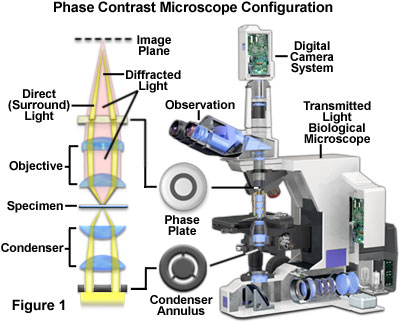
[[Image:fáziskontraszt-mikroszkóp.png|center|thumb|400px|A fáziskontraszt-mikroszkóp vázlatos képe]]
 +
 +
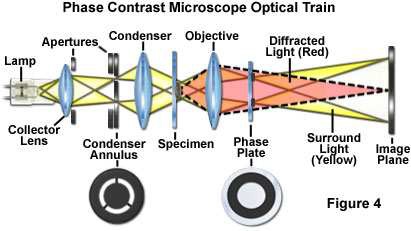
A kondenzorlencse<ref>[http://hu.wikipedia.org/wiki/F%C3%A1ziskontraszt-mikroszk%C3%B3p Fáziskontraszt mikroszkóp (Wikipédia)]</ref> alá olyan átlátszatlan lemezt helyeznek, amelyen a fényzáró réteg gyűrű alakú áteresztő területet tartalmaz („gyűrű-diafragma”). A kondenzorból a preparátum felé kilépő sugár ezért henger- vagy kúppalást mentén halad át a tárgyon, majd képeződik le az objektív gyújtópontjában. Az objektív felett gyűrű alakú rápárologtatott réteget tartalmazó lemez van, amely a hengerpalást mentén jövő (összehasonlító) fénysugarat a hullámhossz negyedrészével fázisban eltolja („fázislemez”). A vizsgálandó preparátum optikailag sűrűbb részleteiből jövő, fáziskésést szenvedett tört sugarak nem haladnak át a fázisgyűrűn és a képsíkban egyesülnek az összehasonlító sugarakkal, interferálnak azokkal. Ez ahhoz vezet, hogy a sugarak kioltják (vagy vastagabb struktúrák esetén erősítik) egymást, miáltal a tárgy különböző törésmutatójú és vastagságú komponensei különböző mértékben sötétnek (esetleg világosnak látszanak). A fázislemez azt a célt szolgálja, hogy az aránylag kis fáziskésést szenvedett sugarak esetén is aránylag nagy legyen a fáziskülönbség és így a kontraszt.
 +
 +
[[Image:fáziskontraszt-mikroszkóp_sugármenet.png|center|thumb|500px|A mikroszkóp sugármenetének vázlatos képe]]
  
 
==Interferencia mikroszkópia==
 
==Interferencia mikroszkópia==
40. sor: 119. sor:
  
 
==Hivatkozások==
 
==Hivatkozások==
 +
<references />

A lap jelenlegi, 2011. december 22., 16:30-kori változata

Az alábbi órán a különböző kísérleti technikák működési elvével foglalkoztunk. Fontos tudni, hogy a jelen órán vizsgált rendszereknél a válasz nem lineáris a perturbációval, azaz ha van két megoldásunk, akkor ezek lineárkombinációja nem lesz megoldás. A továbbiakban ezen az órán olyan technikákkal fogunk foglalkozni, amelyek segítségével a kis amplitudójú, vagy bonyolult geometriájú esetben a térbeli struktúrákat láthatóvá lehet tenni.

Kísérleti technikák

A következő technikákkal foglalkozunk az alábbiakban:

  • Árnyékleképezés (shadowgraph), schlieren technika
  • Polarizációs mikroszkópia (kettőstörés), fáziskontraszt és interferencia mikroszkópia
  • Periodikus struktúrák detektálása diffrakcióval (helyérzékeny fotodetektorok)
  • Sebességmérés áramlásokban (Particle Image Velocimetry - PIV, Particle Tracking)
  • Nem átlátszó rendszerek belsejében lejátszódó jelenségek vizualizálása (index matching, PEPT, DWS, MRI, CT)
  • CCD és CMOS szenzorok tulajdonságai

Árnyékleképezés (shadowgraph)

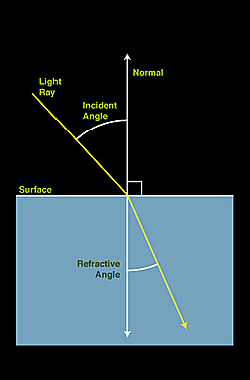
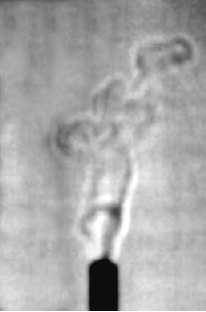
Lényege: intenzív, monokromatikus fényforrással optikai inhomogenitások árnyékképét hozzuk létre. A jelenség alapja, hogy a fény az optikailag sűrűbb közeg felé törik (hajlik el - lásd lentebb a bal oldali ábrát). Egy inhomogén optikai közeg (például egy gyertyaláng) különböző részei fókuszálják, más részei pedig defókuszálják a beérkező fénynyalábot, így kialakul egy árnyékkép. Az árnyékkép alakjából pedig következtetni tudunk a megfigyelt minta sűrűségeloszlására. Természetesen ez a technika csak optikailag átlátszó közegek esetén (pl. levegő, víz, üveg) alkalmazható.

  • A fénytörés jelensége

  • Gradiens indexű lencse fényfókuszálása

  • Az autó fölött "fodrozódó" levegő is a fent ismertetett hatás következménye

  • A gyertyaláng árnyékképe

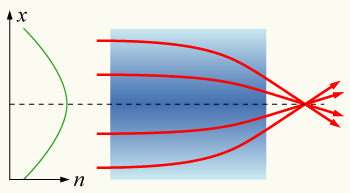
A fenti, balról a második ábrán látható gradiens indexű lencse (gradient index lens) éppen úgy fókuszálja (vagy defókuszálja) a fényt, ahogy az árnyékleképezés során az inhomogén anyagok keresztülhaladó fénnyel is történik. A lencse működését a fenti ábra jól szemlélteti. Egy egyszerű, (például) kocka alakú tárgyról van szó, melynek törésmutatója inhomogén és így a domború lencsékhez hasonlóan fókuszálja a fényt.

Példa: Rayleigh-Bénard áramlás vizualizálása

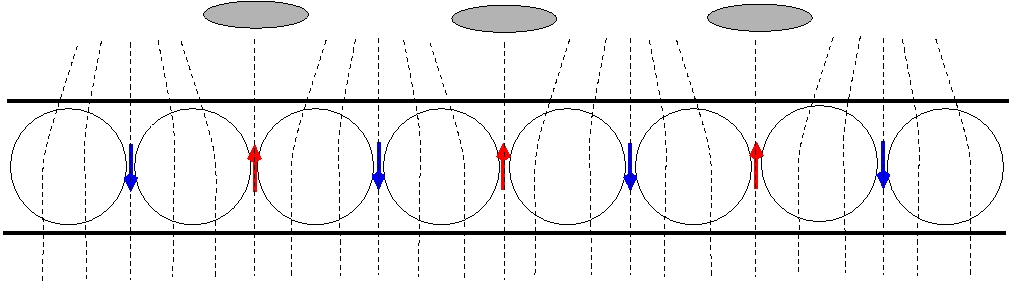
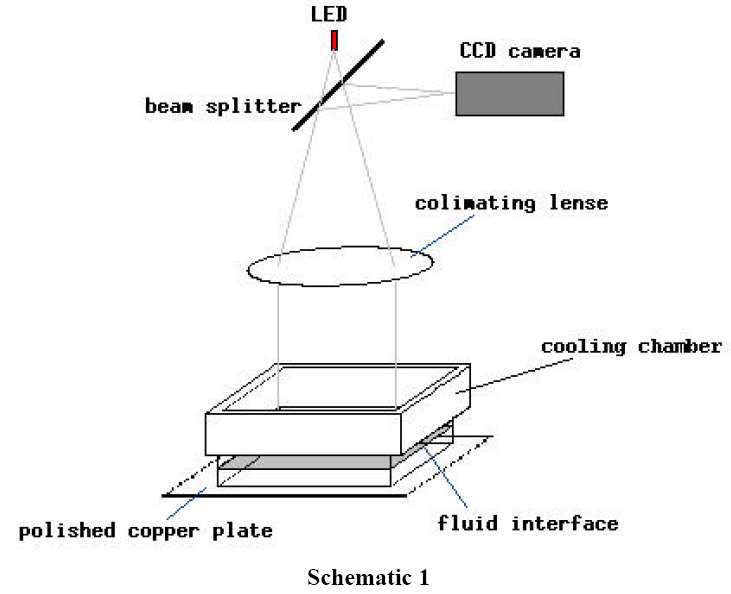
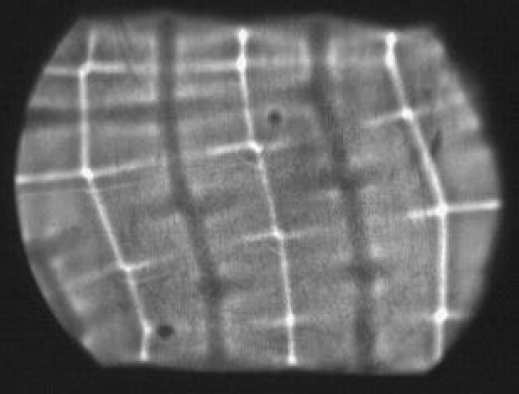
Az árnyékleképezés bemutatására jó példa az alulról fűtött folyadékban (pl. szilikonolaj) kialakuló Rayleigh-Bénard áramlás. Ha elég nagy a függőleges hőmérséklet-gradiens (a pontos képletet egy későbbi órán), folyadékáramlás indul meg. Az alul lévő melegebb (emiatt kisebb sűrűségű) anyag fölfelé, míg a fölül lévő hidegebb (emiatt nagyobb sűrűségű) anyag lefelé igyekszik. Így kialakulhat egy körkörös föl- és leáramlás.

  • A Rayleigh-Bénard áramlás vizualizálása árnyékleképezéssel

  • Az áramlás oldalnézetből

  • A berendezés vázlatos képe

  • Az áramlás árnyékképe felülről, 1 cm vastag olajréteg esetén, 1oC-os hőmérsékletkülönbségnél.

Árnyékleképezés napfénnyel

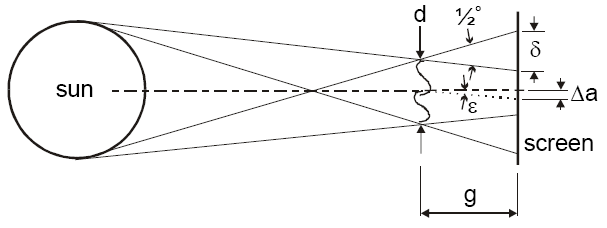
A Nap, mint fényforrás előnyei, hogy intenzív és nagyon nagy objektumokra is alkalmazható. Hátránya, hogy nem pontszerű, emiatt a keletkező kép széle elmosódott lesz. A felbontási küszöböt az alábbi vázlatos ábra alapján a következő egyenletekkel becsüljük.

A Nap, mint fényforrás alkalmazása során a felbontási küszöb becslése

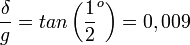
\frac{\delta}{g} = tan \left( \frac{1}{2}^o \right) = 0,009
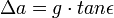
\Delta a = g \cdot tan \epsilon
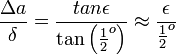
\frac{\Delta a}{\delta} = \frac{tan \epsilon}{\tan \left( \frac{1}{2}^o \right)} \approx \frac{\epsilon}{\frac{1}{2}^o}

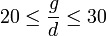A fenti képletekből látható, hogy túl nagy, vagy túl kicsi relatív ernyőtávolság \left( \frac{g}{d} \right) esetén nem lesz jó a kép. Az optimális távolság: 20 \le \frac{g}{d} \le 30 között van.

Schlieren technika

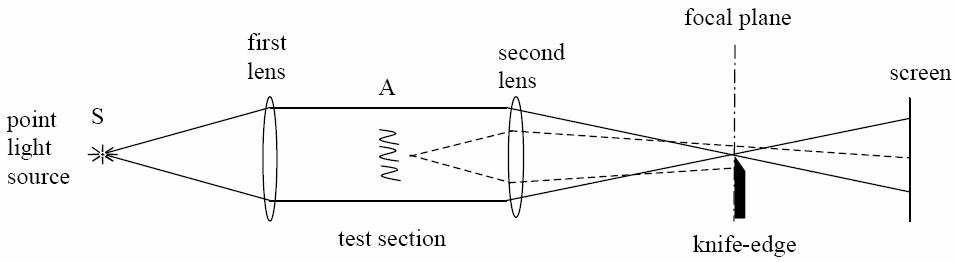
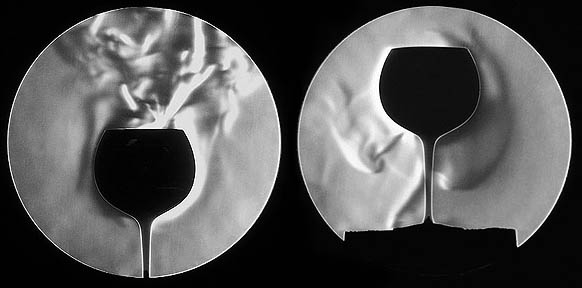
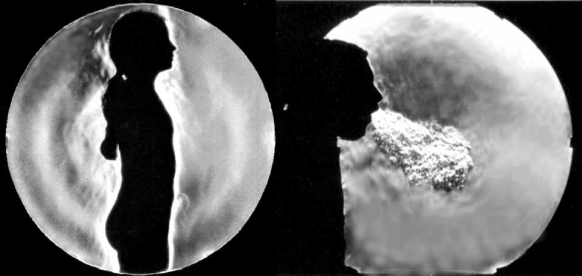
A Schliere-technikával működő berendezés vázlatos képe

A Schlieren-technika segítségével optikailag átlátszó anyagban vizsgálhatunk kis sűrűség-inhomogenitásokat. A technika lényege, hogy az "A" helyen lévő kis sűrűség-inhomogenitást úgy jelenítjük meg, hogy a párhuzamos nyalábot összefókuszáló lencse gyújtópontjába egy pengét tolunk. Ha az "A" helyen lévő közeg teljesen homogén, akkor a kép hirtelen tűnik el, amikor a penge a fókuszpontba ér. Ha azonban az "A" helyen lévő közeg inhomogén, akkor a penge betolásával az ernyőn folytonosan változik a kép, és a direkt nyalábot kitakarva az inhomogenitás jól láthatóvá válik.

  • Néhány példa a Shlieren-technikával történő ábrázolásra

  • Borospohár körül áramló gáz képe

  • Az emberi lehellet képe

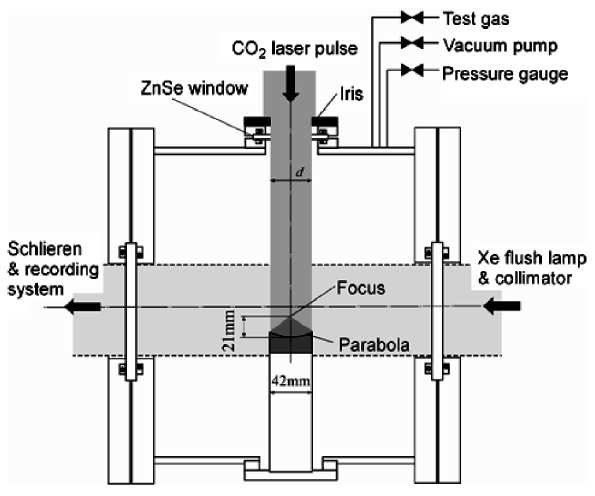
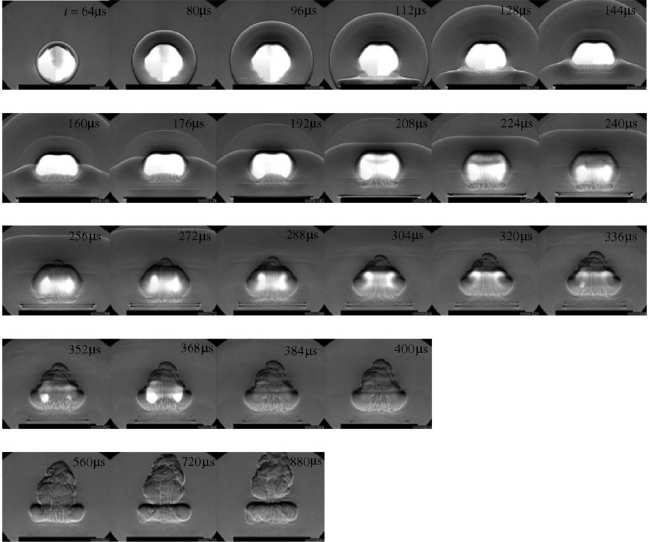
Plazmabuborék határán fellépő Richtmyer-Meshkov instabilitás vizualizálása Schlieren-technikával

Egy függőleges cső aljában parabolatükröt helyeznek el. A fölülről érkező nyalábot a tükör fókuszálja, ennek következtében a csőben lévő gázban egy plazmabuborék jön létre (az alábbi, jobb oldali képen fehér tartomány). A buborék keletkezésekor egy lökéshullám indul meg gömb alakban kifelé, mely a parabolatükörről visszaverődve párhuzamos hullámfrontként halad előre, majd nekiütközik magának a buboréknak, aminek határa a lökéshullámmal való kölcsönhatás következtében instabillá válik (112 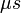\mu s): kialakul az úgynevezett Richtmyer-Meshkov instabilitás (mely a Rayleigh-Taylor instabilitás egy formája, mindkettőről szó lesz a 4. órán).

  • A Richtmyer-Meshkov instabilitás vizualizálása Schlieren-technikával

  • A berendezés vázlatos képe

  • A plazmabuborékról készült képek

Polarizációs mikroszkópia (kettőstörés)

Bizonyos kristályokban a lineárisan poláros fény sebessége függ attól, hogy melyik kristálytengely irányában halad. Ennek oka az, hogy az anyag anizotróp, és különböző mértékben polarizálható a különböző irányokban.

A különböző polarizációk szemléltetése

Kettőstörés: A (kettőstörő) kristályba belépő fény két sugárra bomlik, amelyek közül az egyik, az úgynevezett rendes vagy ordinárius sugár szabály szerint követi a törés törvényét, a másik, a rendellenes vagy extraordinárius sugár azonban nem. Így törik meg a rendes sugár és a rendellenes sugár a kettős töréskor.

A jelenség azzal magyarázható, hogy míg a rendes (ordinárius - o) sugár esetén a hullámfront pontjaiból rendes kör- (gömb)hullámok indulnak ki, a rendellenes (extraordinárius - e) sugár esetén ezek az elemi hullámok ellipszis alakot vesznek fel, aminek az az oka, hogy a kristály szerkezete miatt a kristályban az adott irányban megváltozik a fény terjedési sebessége. A rendellenes (eo) sugár esetén a törésmutató a beeső sugár irányától is függ, és (a törés törvényével szemben) a megtört sugár általában nem marad a beesési síkban.

Egytengelyű kristályokban általános esetben az optikai tengely és a nyaláb iránya jelöli ki az ordinárius és extraordinárius nyalábok vibrációs irányát. A mteszetet, ami mindkét nyalábot tartalmazza, fősíknak (principal section) nevezzük. Az ordinárius nyalábban a tér a fősíkra merőlegesen, míg az extraordinárius nyalábban a fősíkban oszcillál.

A törésmutató anizotrópia az extraordinárius (az optikai tengellyel párhuzamos polarizációjú) és az ordinárius (a tengelyre merőleges polarizációjú) nyalábokra vonatkozó törésmutatók különbsége: 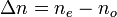\Delta n = n_e - n_o

  • A kettőstörést szemléltető ábrák

  • Az ordinárius és extraordinárius nyalábok szemléltetése

  • A fősík szemléltetése

  • Kettőstörés kalcitban

  • Vizuális példa a kettőstörésre

A kettőstörő anyag a két nyaláb (o és e) fázisát eltolja egymáshoz képest. Így a bejövő lineárisan poláros fény a mintát elhagyva általában elliptikusan poláros lesz. Ez a jelenség a kettőstörő anyagokban jól használható orientációs inhomogenitások vizsgálatára és azok időbeli változásának nyomon követésére - méghozzá polarizátorokkal felszerelt mikroszkóp segítségével.

A polarizációs mikroszkóp vázlatos felépítése

A mikroszkópba vékony 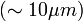\left( \sim 10 \mu m \right) szeletet téve a különböző orientációjú domének különböző mértékeben tolják el a két (o és e) nyaláb fázisát, így különböző színük (illetve monokromatikus fény esetén különböző intenzitásuk) lesz.

Megfelelően polarizált nyalábot használva a kettőstörő anyag árnyékleképezése optimalizálható.

  • Példák a polarizációs mikroszkóppal készült felvételekre

  • Vitamin kristály

  • A folyadékkristály optikai mintázatai

  • Nematikus folyadékkristályban nyírás hatására kialakult hengeres áramlás képe

Fáziskontraszt mikroszkópia

A fáziskontraszt-mikroszkóp vázlatos képe

A kondenzorlencse[1] alá olyan átlátszatlan lemezt helyeznek, amelyen a fényzáró réteg gyűrű alakú áteresztő területet tartalmaz („gyűrű-diafragma”). A kondenzorból a preparátum felé kilépő sugár ezért henger- vagy kúppalást mentén halad át a tárgyon, majd képeződik le az objektív gyújtópontjában. Az objektív felett gyűrű alakú rápárologtatott réteget tartalmazó lemez van, amely a hengerpalást mentén jövő (összehasonlító) fénysugarat a hullámhossz negyedrészével fázisban eltolja („fázislemez”). A vizsgálandó preparátum optikailag sűrűbb részleteiből jövő, fáziskésést szenvedett tört sugarak nem haladnak át a fázisgyűrűn és a képsíkban egyesülnek az összehasonlító sugarakkal, interferálnak azokkal. Ez ahhoz vezet, hogy a sugarak kioltják (vagy vastagabb struktúrák esetén erősítik) egymást, miáltal a tárgy különböző törésmutatójú és vastagságú komponensei különböző mértékben sötétnek (esetleg világosnak látszanak). A fázislemez azt a célt szolgálja, hogy az aránylag kis fáziskésést szenvedett sugarak esetén is aránylag nagy legyen a fáziskülönbség és így a kontraszt.

A mikroszkóp sugármenetének vázlatos képe

Interferencia mikroszkópia

Periodikus struktúrák detektálása diffrakcióval (helyérzékeny fotodetektorok)

Sebességmérés áramlásokban (Particle Image Velocity - PIV)

Sebességmérés áramlásokban (Particle Tracking)

Nem átlászó rendszerek belsejében lejátszódó jelenségek vizualizálása (index matching)

Nem átlászó rendszerek belsejében lejátszódó jelenségek vizualizálása (PEPT, DWS, MRI, CT)

CCD és CMOS szenzorok tulajdonságai

<<<Vissza az óra nyitólapjára

Hivatkozások

  1. ↑ Fáziskontraszt mikroszkóp (Wikipédia)
A lap eredeti címe: „http://tetelwiki.mafihe.hu/index.php?title=Mintázat_2.óra&oldid=1445”