„Atom- és molekulafizika” változatai közötti eltérés
(Új oldal, tartalma: „Az atom- és molekulafizika előadás és gyakorlat oldala ==A tárgyhoz kapcsolódó dokumentumok== [http://www.complex.elte.hu/~csordas/eloadas1.pdf Vetített diák 1.]…”) |
(→A tárgyhoz kapcsolódó dokumentumok) |
||
| (9 közbenső módosítás, amit 5 másik szerkesztő végzett, nincs mutatva) | |||
| 5. sor: | 5. sor: | ||
[http://www.complex.elte.hu/~csordas/eloadas4.pdf Vetített diák 2.] | [http://www.complex.elte.hu/~csordas/eloadas4.pdf Vetített diák 2.] | ||
| + | |||
| + | ==Gyakorlati összefoglaló== | ||
| + | |||
| + | ===A alapállapoti energia szintek számolása=== | ||
| + | |||
| + | Az atomok energiaszintjeit a Schrödinger-egyeneltből számoljuk: | ||
| + | |||
| + | <math>H\Phi = E\Phi \,</math> | ||
| + | |||
| + | A Hidrogén-szerű egyrészecske Hamilton operátorban kinetikus enrgia szerepel és Coulomb-potenciál: | ||
| + | |||
| + | <math>H = -\frac{\hbar^2}{2m} \Delta -\frac{Ze_0^2}{r_0} \,</math> | ||
| + | |||
| + | ahol ''Z'' a rendszám, <math>e_0</math> a redukált töltés, ''m'' a redukált tömeg, közelítőleg az elektron tömege, ''Z'' a mag rendszáma. Az alapállapoti energia sajátértékek: | ||
| + | |||
| + | <math>E_{nlm} = -\frac{1}{2}\frac{Z^2 e_0^2}{a_0}\frac{1}{n^2}</math> | ||
| + | |||
| + | ahol ''n'' a főkvantumszám, értéke 0, 1, 2, ..., ''l'' a mellékkvantumszám, értéke 0-tól (n-1)-ig lehetséges, egyesével, és ''m'' a mágneses kvantunmszám, értéke (-''l'')-től (+''l'')-ig lehetséges egyesével. | ||
| + | |||
| + | A hullámfüggvényt sugár- és szögfüggő tényezőkre szeparálhatjuk: | ||
| + | |||
| + | <math>\Phi_{nlm}(\mathbf{r}) = R_{nl}(r) \cdot Y_l^m(\theta, \phi)</math> | ||
| + | |||
| + | ===Többelektronos rendszerek=== | ||
| + | ====A alapállapoti perturbálatlan eset==== | ||
| + | |||
| + | A több elektront tartalmazó atomok elektronszerkezetét elsőrendű perturbációs módszerrel kezeljük, ahol az elektronok kölcsönhatása adja a perturbációs Hamilton operátort. He szerű atomra: | ||
| + | |||
| + | <math>H = H_0 + H_1 = H_0 + \frac{e_0^2}{r_{12}}</math> | ||
| + | |||
| + | A többrészecskés esetben a perturbálatlan Hamilton(He atomra N=2): | ||
| + | |||
| + | <math>H_0 = \sum_{i=1}^{N} -\frac{\hbar^2}{2m_i} \Delta_i -\frac{Ze_0^2}{r_i}</math> | ||
| + | |||
| + | Az alapállapoti hullámfüggvényt kereshetjük ismét szorzat alakban, azonban vegyük figyelembe a spint is: | ||
| + | |||
| + | <math>\Psi_0 = \Phi_{100}(\mathbf{r_1}) \cdot \Phi_{100}(\mathbf{r_2}) \cdot \chi( s_1, s_2 ) </math> | ||
| + | |||
| + | Alapállapotban ez megtehető, mert a spintényező antiszimmetrikus, a hely- és szögfüggő rész szimmetrikus (ez kötelező alapállapotban), így az eredő hullámfüggvény antiszimmetrikus összhangban a Pauli-elvvel. Továbbá, mivel a tekintett Hamilton-operátor nem függ a spintől, ezért a számolások során ez mindig kihozható az integrálok alól, és a skaláris szorzat számolása során az ortonormalitás miatt 1-et ad. | ||
| + | |||
| + | Az alapállapoti energia ekkor: | ||
| + | |||
| + | <math>E_0 = \langle\Psi_0|H|\Psi_0\rangle = \langle\Psi_0|H_0|\Psi_0\rangle + \langle\Psi_0|H_1|\Psi_0\rangle = E_0^0 + E_0^1 \,</math> | ||
| + | |||
| + | Az első tag a két Hidrogén-szerű alapállapot (n=1) energiasajátértékének összege, ezért: | ||
| + | |||
| + | <math>E_0^0 = 2 \cdot -\frac{1}{2}\frac{Z^2 e_0^2}{a_0}</math> | ||
| + | |||
| + | ====A alapállapoti perturáció==== | ||
| + | Az elektron-elektron kölcsönhatási perturbáció számolása: | ||
| + | |||
| + | <math>E_0^1 = \langle\Psi_0|H_1|\Psi_0\rangle = \int d^3 r_1 \int d^3 r_2 \Phi_{100}(\mathbf{r_1})^* \Phi_{100}(\mathbf{r_2})^* \frac{e_0^2}{r_{12}} \Phi_{100}(\mathbf{r_1}) \Phi_{100}(\mathbf{r_2})</math> | ||
| + | |||
| + | ahol a spint már kiösszegeztük. A további lépések: | ||
| + | * Beírjuk a szorzat alakú hullámfüggvényt. | ||
| + | * A <math>d^3 r</math> integrálási változók helyett gömbi koordinátákra térünk át: <math>dr r^2 d\Omega\,</math> | ||
| + | * Beírjuk <math>\frac{1}{r_{12}}</math> helyére a gömbfüggvények szerinti összegképletet. Ebben a kifejtésben a gömbfüggvények különböző argumentummal szerepelnek a szumma alatt, ezért beviszünk mindkettőhöz 1-1 hozzátartozó argumentumú gömbfüggvényt a hullámfüggvényekből, és a szumma alatt kiintegráljuk, ami az ortonormalitás miatt Kronecker-deltákat eredményez, így a szummák elvégezhetőek, és ''l'' konkrét értéket vesz fel. A kint maradt gömbfüggvények m=0,l=0 értékekhez tartoznak, azaz értékük <math>\frac{1}{\sqrt{4\pi}}</math> | ||
| + | *Ekkor már csak a sugár függő integrálok maradnak, amelyek <math>\int x^2 e^{-x}</math> alakúak, és analitikusan kiszámolhatóak. | ||
| + | |||
| + | ===Hélium-szerű gerjesztett állapotok=== | ||
| + | A kételektron rendszereknek azon gerjesztéseit tekintjük, amelyeknél csak az egyik elektron van az alapállapotnál magasabban, a másik alapállapotban: | ||
| + | |||
| + | <math> \Psi_a(1) = \Phi_{100}(\mathbf{r_1}) </math> | ||
| + | |||
| + | <math> \Psi_b(2) = \Phi_{2lm}(\mathbf{r_2}) </math> | ||
| + | |||
| + | Ez azért jogos, mert ha mindkettő magasabb szinten lenne, az már nem lenne kötött állapot. Ekkor már tlejesíthető a Pauli-elv két féle kombináció esetén: szimmetrikus a helyfüggvény és antiszimmetrikus a spin függvény(szinglet, mert csak egyilyen spinállapot van) VAGY antiszimmetrikus a helyfüggvény és szimmetrikus a spin függvény(triplet, mert három ilyen spinllapot van). | ||
| + | |||
| + | A hullámfüggvény alakja tehát triplet esetben: | ||
| + | <math>\Psi_{0, triplet} = \frac{1}{\sqrt{2}}\left(\Phi_a(1)\Phi_b(2) - \Phi_a(2)\Phi_b(1) \right) \cdot ^3\chi(s_1, s_2)</math> | ||
| + | |||
| + | A hullámfüggvény alakja szinglet esetben: | ||
| + | <math>\Psi_{0, szinglet} = \frac{1}{\sqrt{2}}\left(\Phi_a(1)\Phi_b(2) + \Phi_a(2)\Phi_b(1) \right) \cdot ^1\chi(s_1, s_2)</math> | ||
| + | |||
| + | ====A perturbálatlan eset==== | ||
| + | A perturbálatlan eset most is a Hidrogén-szerű energiaértékekből számolható: | ||
| + | |||
| + | <math>E_1^0 = E_{100} + E_{200} = -\frac{Z^2 e_0^2}{2a_0}\left( \frac{1}{1^2} + \frac{1}{2^2} \right)</math> | ||
| + | |||
| + | ====A perturbált eset==== | ||
| + | A főbb lépések: | ||
| + | |||
| + | * A spin ismét kiösszegezhető, és 1-et ad. | ||
| + | * Az hullámfüggvényben levő összeget (vagy különbséget) felbontjuk négy tagra a skalárszorzatban. Ebből a vegyes tagok azonosak egy változó csere erejéig, ezért összevonhatóak, hasonlóan a négyzetes tagok is, így két integrált kapunk: egy Kicserélődési és egy Coulomb integrált: | ||
| + | |||
| + | <math>C_{ab} = e_0^2 \int d^3 r_1 \int d^3 r_2 \frac{|\Phi_{a1}|^2 |\Phi_{b2}|^2}{r_{12}}</math> | ||
| + | |||
| + | <math>K_{ab} = e_0^2 \int d^3 r_1 \int d^3 r_2 \frac{\Phi_{a1}^* \Phi_{b1} \Phi_{b2}^* \Phi_{a2}}{r_{12}}</math> | ||
| + | |||
| + | * Beírjuk a szorzat alakú hullámfüggvényt. | ||
| + | * A <math>d^3 r</math> integrálási változók helyett gömbi koordinátákra térünk át: <math>dr r^2 d\Omega\,</math> | ||
| + | * Beírjuk <math>\frac{1}{r_{12}}</math> helyére a gömbfüggvények szerinti összegképletet. Bevisszük az integrálokat a szumma alá, és csoportosítjuk az azonos argumentumú gömbfüggvényeket. Ezeket vagy a norma, vagy az ortogonalitás segítségével elvégezzük. Az összegző kvantumsázmok értéke meghatározódik, és helyükbe a meghatározandó gerjesztett pálya kvantumszámai írhatóak. | ||
| + | * A hátramaradó integrálok <math>\int x^n e^{-x}</math> alakúak, és elvégezhetőek. | ||
| + | |||
| + | [[Kategória: Atom- és molekulafizika]] | ||
| + | [[Kategória: MSc]] | ||
A lap jelenlegi, 2014. december 4., 15:45-kori változata
Az atom- és molekulafizika előadás és gyakorlat oldala
Tartalomjegyzék
A tárgyhoz kapcsolódó dokumentumok
Gyakorlati összefoglaló
A alapállapoti energia szintek számolása
Az atomok energiaszintjeit a Schrödinger-egyeneltből számoljuk:
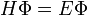
A Hidrogén-szerű egyrészecske Hamilton operátorban kinetikus enrgia szerepel és Coulomb-potenciál:
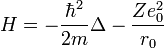
ahol Z a rendszám, 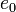 a redukált töltés, m a redukált tömeg, közelítőleg az elektron tömege, Z a mag rendszáma. Az alapállapoti energia sajátértékek:
a redukált töltés, m a redukált tömeg, közelítőleg az elektron tömege, Z a mag rendszáma. Az alapállapoti energia sajátértékek:
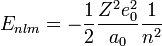
ahol n a főkvantumszám, értéke 0, 1, 2, ..., l a mellékkvantumszám, értéke 0-tól (n-1)-ig lehetséges, egyesével, és m a mágneses kvantunmszám, értéke (-l)-től (+l)-ig lehetséges egyesével.
A hullámfüggvényt sugár- és szögfüggő tényezőkre szeparálhatjuk:
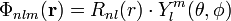
Többelektronos rendszerek
A alapállapoti perturbálatlan eset
A több elektront tartalmazó atomok elektronszerkezetét elsőrendű perturbációs módszerrel kezeljük, ahol az elektronok kölcsönhatása adja a perturbációs Hamilton operátort. He szerű atomra:
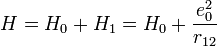
A többrészecskés esetben a perturbálatlan Hamilton(He atomra N=2):
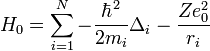
Az alapállapoti hullámfüggvényt kereshetjük ismét szorzat alakban, azonban vegyük figyelembe a spint is:
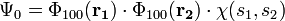
Alapállapotban ez megtehető, mert a spintényező antiszimmetrikus, a hely- és szögfüggő rész szimmetrikus (ez kötelező alapállapotban), így az eredő hullámfüggvény antiszimmetrikus összhangban a Pauli-elvvel. Továbbá, mivel a tekintett Hamilton-operátor nem függ a spintől, ezért a számolások során ez mindig kihozható az integrálok alól, és a skaláris szorzat számolása során az ortonormalitás miatt 1-et ad.
Az alapállapoti energia ekkor:
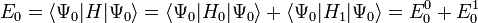
Az első tag a két Hidrogén-szerű alapállapot (n=1) energiasajátértékének összege, ezért:
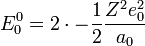
A alapállapoti perturáció
Az elektron-elektron kölcsönhatási perturbáció számolása:
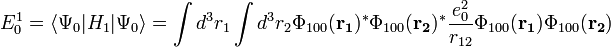
ahol a spint már kiösszegeztük. A további lépések:
- Beírjuk a szorzat alakú hullámfüggvényt.
- A
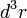 integrálási változók helyett gömbi koordinátákra térünk át:
integrálási változók helyett gömbi koordinátákra térünk át: 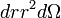
- Beírjuk
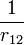 helyére a gömbfüggvények szerinti összegképletet. Ebben a kifejtésben a gömbfüggvények különböző argumentummal szerepelnek a szumma alatt, ezért beviszünk mindkettőhöz 1-1 hozzátartozó argumentumú gömbfüggvényt a hullámfüggvényekből, és a szumma alatt kiintegráljuk, ami az ortonormalitás miatt Kronecker-deltákat eredményez, így a szummák elvégezhetőek, és l konkrét értéket vesz fel. A kint maradt gömbfüggvények m=0,l=0 értékekhez tartoznak, azaz értékük
helyére a gömbfüggvények szerinti összegképletet. Ebben a kifejtésben a gömbfüggvények különböző argumentummal szerepelnek a szumma alatt, ezért beviszünk mindkettőhöz 1-1 hozzátartozó argumentumú gömbfüggvényt a hullámfüggvényekből, és a szumma alatt kiintegráljuk, ami az ortonormalitás miatt Kronecker-deltákat eredményez, így a szummák elvégezhetőek, és l konkrét értéket vesz fel. A kint maradt gömbfüggvények m=0,l=0 értékekhez tartoznak, azaz értékük 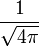
- Ekkor már csak a sugár függő integrálok maradnak, amelyek
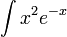 alakúak, és analitikusan kiszámolhatóak.
alakúak, és analitikusan kiszámolhatóak.
Hélium-szerű gerjesztett állapotok
A kételektron rendszereknek azon gerjesztéseit tekintjük, amelyeknél csak az egyik elektron van az alapállapotnál magasabban, a másik alapállapotban:
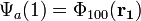
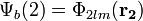
Ez azért jogos, mert ha mindkettő magasabb szinten lenne, az már nem lenne kötött állapot. Ekkor már tlejesíthető a Pauli-elv két féle kombináció esetén: szimmetrikus a helyfüggvény és antiszimmetrikus a spin függvény(szinglet, mert csak egyilyen spinállapot van) VAGY antiszimmetrikus a helyfüggvény és szimmetrikus a spin függvény(triplet, mert három ilyen spinllapot van).
A hullámfüggvény alakja tehát triplet esetben:
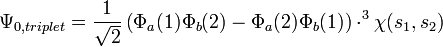
A hullámfüggvény alakja szinglet esetben:
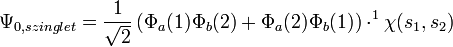
A perturbálatlan eset
A perturbálatlan eset most is a Hidrogén-szerű energiaértékekből számolható:
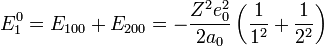
A perturbált eset
A főbb lépések:
- A spin ismét kiösszegezhető, és 1-et ad.
- Az hullámfüggvényben levő összeget (vagy különbséget) felbontjuk négy tagra a skalárszorzatban. Ebből a vegyes tagok azonosak egy változó csere erejéig, ezért összevonhatóak, hasonlóan a négyzetes tagok is, így két integrált kapunk: egy Kicserélődési és egy Coulomb integrált:
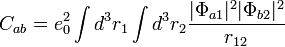
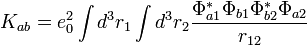
- Beírjuk a szorzat alakú hullámfüggvényt.
- A
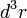 integrálási változók helyett gömbi koordinátákra térünk át:
integrálási változók helyett gömbi koordinátákra térünk át: 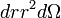
- Beírjuk
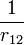 helyére a gömbfüggvények szerinti összegképletet. Bevisszük az integrálokat a szumma alá, és csoportosítjuk az azonos argumentumú gömbfüggvényeket. Ezeket vagy a norma, vagy az ortogonalitás segítségével elvégezzük. Az összegző kvantumsázmok értéke meghatározódik, és helyükbe a meghatározandó gerjesztett pálya kvantumszámai írhatóak.
helyére a gömbfüggvények szerinti összegképletet. Bevisszük az integrálokat a szumma alá, és csoportosítjuk az azonos argumentumú gömbfüggvényeket. Ezeket vagy a norma, vagy az ortogonalitás segítségével elvégezzük. Az összegző kvantumsázmok értéke meghatározódik, és helyükbe a meghatározandó gerjesztett pálya kvantumszámai írhatóak. - A hátramaradó integrálok
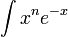 alakúak, és elvégezhetőek.
alakúak, és elvégezhetőek.