„Magfizika” változatai közötti eltérés
a (→AMU) |
|||
| (7 közbenső módosítás ugyanattól a szerkesztőtől nincs mutatva) | |||
| 4. sor: | 4. sor: | ||
*A korábbi évek feladatinak kidolgozása pdf-ben: [[fájl:magfiz.pdf|ez lenne az]] | *A korábbi évek feladatinak kidolgozása pdf-ben: [[fájl:magfiz.pdf|ez lenne az]] | ||
| + | |||
| + | ==Magfizika tételkidolgozás (a korábbi évek feladatsorainak zanzásított, típus szerinti megoldásai)== | ||
| + | ===Izotópok=== | ||
| + | '''a) Milyen eredetűek a környezetünkben előforduló radioaktív atommagok? b) Sorolja fel a természetben előforduló radioaktív családokat!''' | ||
| + | a) A környezetünkbe nelőforduló radioaktív atommagok: | ||
| + | ::a.1. Hosszú felezési idejű izotópok, pl: <sup>40</sup><sub>19</sub>K (<math>1,28 \cdot 10^9</math> év – 0.012%); <sup>87</sup><sub>37</sub>Rb (<math>4,7\cdot 10^{10} </math>év – 27.83%); <sup>113</sup><sub>48</sub>Cd (<math>9\cdot 10^{15}</math> év – 12.3%); <sup>115</sup><sub>49</sub>In (<math>5\cdot 10^{14}</math> év – 95.7%);<math>^{208}_{82}</math>Pb (52.4%); <math>^{206}_{82}</math>Pb (24.1%); <sup>207</sup><sub>82</sub>Pb (22.1%) | ||
| + | ::a.2. Folyamatosan keletkező izotópok, pl: | ||
| + | :::• <sup>3</sup>H (12.3 év – ß- [E<sub>max</sub>=18.6 keV]), folyamatok: <sup>14</sup>N(n,t)<sup>12</sup>C és <sup>16</sup>O(n,t)<sup>14</sup>N, keletkezési seb. ~ 0,25 atom/<math>(cm^2\cdot s)</math>, egyensúlyi mennyiség az atmoszférában: ~4 kg, egyenetlen eloszlású, nem keveredik gyorsan | ||
| + | :::• <sup>14</sup><sub>6</sub>C (5730 év – ß- [E<sub>max</sub>=156 keV]), folyamat: <sup>14</sup>N(n,p)<sup>14</sup>C, 2 atom/(cm2.s) évente ~ 7 kg keletkezik, gyorsan keveredik a CO<sub>2</sub>-n keresztül; ~ 56 t egyens. mennyiség a légkörben, élő szervezetben 13.5 Bq/g › kormeghatározás | ||
| + | ::a.3. Civilizációs eredetű, a természetbe kijutott radioaktivitás (nukleáris fegyverkísérletek (1963-ig), nukleáris technika, reaktorok balesetei, stb.), pl: <sup>137</sup><sub>55</sub>Cs (30.07 év); 9038Sr (28.78 év) | ||
| + | b) A természetben előforduló radioaktív családok: | ||
| + | :::• 4n › <sup>232</sup><sub>90</sub>Th (<math>1,4\cdot 10^10</math> év); tórium-sor stabil végmag (=anyaizotóp?) <sup>208</sup><sub>82</sub>Pb (52.4%) | ||
| + | :::• 4n+1 › <sup>237</sup><sub>93</sub>Np (<math>2,2\cdot 10^6</math> év); neptúnium-sor, <sup>209</sup><sub>83</sub>Bi (100%) a rövid felezési idő miatt már elbomlott | ||
| + | :::• 4n+2 › <sup>238</sup><sub>92</sub>U (<math>4,5\cdot 10^9</math> év); urán-sor <sup>206</sup><sub>82</sub>Pb (24.1%) | ||
| + | :::• 4n+3 › <sup>235</sup><sub>92</sub>U (<math>0,7\cdot 10^9</math> év); aktínium-sor, <sup>207</sup><sub>82</sub>Pb (22.1%) | ||
| + | |||
| + | ===Sűrűség=== | ||
| + | ''' a) Milyen módszerekkel lehet meghatározni az alapállapoti magok magsűrűség-eloszlását? b) Írja fel a Woods-Saxon eloszlást, és jellemezze az eloszlás tényleges alakját meghatározó paramétereket! c) Mi az elvi különbség a nagyenergiájú elektronokkal, ill. neutronokkal végrehajtott szóráskísérletekből meghatározott magsűrűség-eloszlások között? d) Hogyan függ a magsugár a tömegszámtól?''' | ||
| + | |||
| + | a) Alapállapoti magok magsűrűség-eloszlásának meghatározása:???????????????????????????????????????????????????????????? | ||
| + | |||
| + | b) Woods-Saxon eloszlás | ||
| + | |||
| + | <math>\rho (r) = \frac{k\cdot \rho_0}{1 + exp\left( \frac{r - R_{\frac{1}{2}}}{a} \right)}</math> | ||
| + | |||
| + | :::• a › diffúzitás: ? 90% és 10% közötti távolsága | ||
| + | :::• <math>R_{\frac{1}{2}}</math> › sűrűség 50% (leggyakrabban) | ||
| + | :::• <math>R = R_0\cdot A^{\frac{1}{3}}</math> › <math>R0 = 1,128 fm</math> › az atommagok sűrűsége ~ állandó --> '''magsugár tömegszám-függése!''' | ||
| + | :::• <math>\rho(0) = 0,17\cdot \frac{Z\cdot e}{A} (fm^{-3})</math> | ||
| + | |||
| + | c) Elvi különbség a magsűrűség-eloszlások között??????????????????????????????????????????????????????????????? | ||
| + | |||
| + | ===Mágikus számok=== | ||
| + | '''a) Sorolja fel a mágikus számokat! b) Mondjon példát egy stabil, kétszer mágikus atommagra! c) Mutasson két jelenségkört, ahol a mágikus számok különleges szerepe megnyilvánul!''' | ||
| + | |||
| + | a) A mágikus számok: 2, 8, 20, 28, 50, 82, 126 | ||
| + | |||
| + | b) Stabil, kétszer mágikus atommag: <sup>16</sup><sub>8</sub>O (99.76%), <sup>40</sup><sub>20</sub>Ca (96.941%),<sup>208</sup><sub>82</sub>Pb (52.4%) | ||
| + | |||
| + | c) Két jelenségkör, ahol a mágikus számok különleges szerepe megnyilvánul:???????????????????????????????????????????????? | ||
| + | |||
| + | ===AMU=== | ||
| + | '''a) Mi az AMU? b) Milyen módszerekkel határozzuk meg az atommagok tömegét és mekkora a meghatározás relatív pontossága? c) Mi a kötési energia definíciója?''' | ||
| + | |||
| + | a) AMU: Atomic Mass Unit (atomi tömegegység), M(<sup>12</sup>C atom) = 12,000 AMU, 1 AMU = <math>1,6605655\cdot 10^{-27}</math> kg = 931,501 MeV. | ||
| + | b) Tömegmeghatározás: | ||
| + | :::* Tömegspektrometria (l. Atomfizika) | ||
| + | |||
| + | :::<math>F = q \cdot \left( E + \frac{1}{c} \cdot [v x B]\right)</math> › forrás – két diszperzív elem – detektálás › M és v meghatározható, kulcskérdés: fókuszálás (irány, seb.), ma: ?M ~ <math>10^{-6}</math> – <math>10^{-7}</math> AMU ›?M/M ~<math>10^{-7}</math> – <math>10^{-9}</math> | ||
| + | |||
| + | :::* Bomlások, bomlási termékek vizsgálata: Ismert: egyik tömeg › rész. azonosítás, energiamérés › bomlástermékek tömege meghatározható; Stabilitástól távoli magok tömegére › pontosság: energiamérés pontosságától függ Felhasznált eszközök: félvezetők, mágneses spektrométerek: ?E ~ keV › ?M ~ <math>10^{-6}</math> AMU › ?M/M ~<math>10^{-8}</math> | ||
| + | |||
| + | :::* Magreakciók kinematikája: Legegyszerűbb: A(B,C)D reakció (általában: B és C könnyű; B bombáz, C kirepül): | ||
| + | <math>M_D\cdot c^2 = (M_A + M_B – M_C)\cdot c^2 + (T_A + T_B) – (T_C – T_D) = (M_A + M_B – M_C)\cdot c^2</math> | ||
| + | |||
| + | <math>T_B</math> › bombázó energia; <math>T_A = 0</math> | ||
| + | Mérendő: <math>T_C</math> és <math>T_D</math>; Ma: sokrészecskés reakciók is; Pontosság: detektálás pontossága; ?M ~ <math>10^{-6}</math> AMU | ||
| + | |||
| + | :::* Az atommagok tömegét magtáblázatokban található adatokból lehet meghatározni, általában nem közvetlenül adják meg. | ||
A lap jelenlegi, 2016. november 22., 12:29-kori változata
Tartalomjegyzék
Elérhető segédanyagok
Magfizika tételkidolgozás (a korábbi évek feladatsorainak zanzásított, típus szerinti megoldásai)
Izotópok
a) Milyen eredetűek a környezetünkben előforduló radioaktív atommagok? b) Sorolja fel a természetben előforduló radioaktív családokat! a) A környezetünkbe nelőforduló radioaktív atommagok:
- a.1. Hosszú felezési idejű izotópok, pl: 4019K (
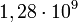 év – 0.012%); 8737Rb (
év – 0.012%); 8737Rb (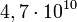 év – 27.83%); 11348Cd (
év – 27.83%); 11348Cd (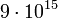 év – 12.3%); 11549In (
év – 12.3%); 11549In (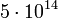 év – 95.7%);
év – 95.7%);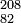 Pb (52.4%);
Pb (52.4%); 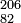 Pb (24.1%); 20782Pb (22.1%)
Pb (24.1%); 20782Pb (22.1%) - a.2. Folyamatosan keletkező izotópok, pl:
- • 3H (12.3 év – ß- [Emax=18.6 keV]), folyamatok: 14N(n,t)12C és 16O(n,t)14N, keletkezési seb. ~ 0,25 atom/
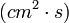 , egyensúlyi mennyiség az atmoszférában: ~4 kg, egyenetlen eloszlású, nem keveredik gyorsan
, egyensúlyi mennyiség az atmoszférában: ~4 kg, egyenetlen eloszlású, nem keveredik gyorsan - • 146C (5730 év – ß- [Emax=156 keV]), folyamat: 14N(n,p)14C, 2 atom/(cm2.s) évente ~ 7 kg keletkezik, gyorsan keveredik a CO2-n keresztül; ~ 56 t egyens. mennyiség a légkörben, élő szervezetben 13.5 Bq/g › kormeghatározás
- • 3H (12.3 év – ß- [Emax=18.6 keV]), folyamatok: 14N(n,t)12C és 16O(n,t)14N, keletkezési seb. ~ 0,25 atom/
- a.3. Civilizációs eredetű, a természetbe kijutott radioaktivitás (nukleáris fegyverkísérletek (1963-ig), nukleáris technika, reaktorok balesetei, stb.), pl: 13755Cs (30.07 év); 9038Sr (28.78 év)
- a.1. Hosszú felezési idejű izotópok, pl: 4019K (
b) A természetben előforduló radioaktív családok:
- • 4n › 23290Th (
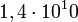 év); tórium-sor stabil végmag (=anyaizotóp?) 20882Pb (52.4%)
év); tórium-sor stabil végmag (=anyaizotóp?) 20882Pb (52.4%) - • 4n+1 › 23793Np (
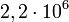 év); neptúnium-sor, 20983Bi (100%) a rövid felezési idő miatt már elbomlott
év); neptúnium-sor, 20983Bi (100%) a rövid felezési idő miatt már elbomlott - • 4n+2 › 23892U (
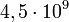 év); urán-sor 20682Pb (24.1%)
év); urán-sor 20682Pb (24.1%) - • 4n+3 › 23592U (
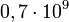 év); aktínium-sor, 20782Pb (22.1%)
év); aktínium-sor, 20782Pb (22.1%)
- • 4n › 23290Th (
Sűrűség
a) Milyen módszerekkel lehet meghatározni az alapállapoti magok magsűrűség-eloszlását? b) Írja fel a Woods-Saxon eloszlást, és jellemezze az eloszlás tényleges alakját meghatározó paramétereket! c) Mi az elvi különbség a nagyenergiájú elektronokkal, ill. neutronokkal végrehajtott szóráskísérletekből meghatározott magsűrűség-eloszlások között? d) Hogyan függ a magsugár a tömegszámtól?
a) Alapállapoti magok magsűrűség-eloszlásának meghatározása:????????????????????????????????????????????????????????????
b) Woods-Saxon eloszlás
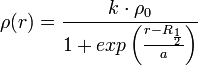
- • a › diffúzitás: ? 90% és 10% közötti távolsága
- •
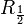 › sűrűség 50% (leggyakrabban)
› sűrűség 50% (leggyakrabban) - •
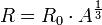 ›
› 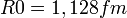 › az atommagok sűrűsége ~ állandó --> magsugár tömegszám-függése!
› az atommagok sűrűsége ~ állandó --> magsugár tömegszám-függése! - •
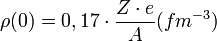
c) Elvi különbség a magsűrűség-eloszlások között???????????????????????????????????????????????????????????????
Mágikus számok
a) Sorolja fel a mágikus számokat! b) Mondjon példát egy stabil, kétszer mágikus atommagra! c) Mutasson két jelenségkört, ahol a mágikus számok különleges szerepe megnyilvánul!
a) A mágikus számok: 2, 8, 20, 28, 50, 82, 126
b) Stabil, kétszer mágikus atommag: 168O (99.76%), 4020Ca (96.941%),20882Pb (52.4%)
c) Két jelenségkör, ahol a mágikus számok különleges szerepe megnyilvánul:????????????????????????????????????????????????
AMU
a) Mi az AMU? b) Milyen módszerekkel határozzuk meg az atommagok tömegét és mekkora a meghatározás relatív pontossága? c) Mi a kötési energia definíciója?
a) AMU: Atomic Mass Unit (atomi tömegegység), M(12C atom) = 12,000 AMU, 1 AMU = 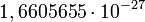 kg = 931,501 MeV.
b) Tömegmeghatározás:
kg = 931,501 MeV.
b) Tömegmeghatározás:
- Tömegspektrometria (l. Atomfizika)
![F = q \cdot \left( E + \frac{1}{c} \cdot [v x B]\right)](/images/math/b/8/c/b8cf2e5b060d3d78db83618937ee94e8.png) › forrás – két diszperzív elem – detektálás › M és v meghatározható, kulcskérdés: fókuszálás (irány, seb.), ma: ?M ~
› forrás – két diszperzív elem – detektálás › M és v meghatározható, kulcskérdés: fókuszálás (irány, seb.), ma: ?M ~ 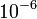 –
– 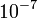 AMU ›?M/M ~
AMU ›?M/M ~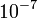 –
– 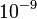
- Bomlások, bomlási termékek vizsgálata: Ismert: egyik tömeg › rész. azonosítás, energiamérés › bomlástermékek tömege meghatározható; Stabilitástól távoli magok tömegére › pontosság: energiamérés pontosságától függ Felhasznált eszközök: félvezetők, mágneses spektrométerek: ?E ~ keV › ?M ~
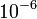 AMU › ?M/M ~
AMU › ?M/M ~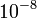
- Bomlások, bomlási termékek vizsgálata: Ismert: egyik tömeg › rész. azonosítás, energiamérés › bomlástermékek tömege meghatározható; Stabilitástól távoli magok tömegére › pontosság: energiamérés pontosságától függ Felhasznált eszközök: félvezetők, mágneses spektrométerek: ?E ~ keV › ?M ~
- Magreakciók kinematikája: Legegyszerűbb: A(B,C)D reakció (általában: B és C könnyű; B bombáz, C kirepül):
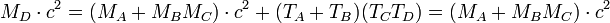
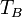 › bombázó energia;
› bombázó energia; 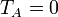 Mérendő:
Mérendő: 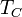 és
és 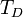 ; Ma: sokrészecskés reakciók is; Pontosság: detektálás pontossága; ?M ~
; Ma: sokrészecskés reakciók is; Pontosság: detektálás pontossága; ?M ~ 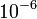 AMU
AMU
- Az atommagok tömegét magtáblázatokban található adatokból lehet meghatározni, általában nem közvetlenül adják meg.
