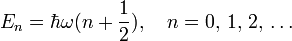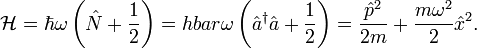„Harmonikus oszcillátor energiája, Hamilton operátora” változatai közötti eltérés
(Új oldal, tartalma: „<math>E_n = \hbar \omega (n + \frac{1}{2}), \quad n=0,\,1,\,2,\, \ldots</math> <math>\mathcal{H} = \hbar \omega (\hat{N} + \frac{1}{2}) = hbar \omega (\hat{a}^{\dagger}\h…”) |
a |
||
| 1. sor: | 1. sor: | ||
<math>E_n = \hbar \omega (n + \frac{1}{2}), \quad n=0,\,1,\,2,\, \ldots</math> | <math>E_n = \hbar \omega (n + \frac{1}{2}), \quad n=0,\,1,\,2,\, \ldots</math> | ||
| − | <math>\mathcal{H} = \hbar \omega (\hat{N} + \frac{1}{2}) = hbar \omega (\hat{a}^{\dagger}\hat{a} + \frac{1}{2})= \frac{\hat{p}^2}{2m} + \frac{m \omega^2}{2}\hat{x}^2.</math> | + | <math>\mathcal{H} = \hbar \omega \left(\hat{N} + \frac{1}{2}\right) = hbar \omega \left(\hat{a}^{\dagger}\hat{a} + \frac{1}{2}\right)= \frac{\hat{p}^2}{2m} + \frac{m \omega^2}{2}\hat{x}^2.</math> |
A lap 2011. június 26., 22:37-kori változata