„Véletlen gráfok generálása, tulajdonságai” változatai közötti eltérés
(→Erdős-Rényi gráf) |
(→Erdős-Rényi gráf) |
||
| 16. sor: | 16. sor: | ||
==Erdős-Rényi gráf== | ==Erdős-Rényi gráf== | ||
| − | N csúcsból áll, minden két csúcs között p valószínűséggel él. Csúcsok növelésével exponenciálisan nő a kapcsolatszám. | + | N csúcsból áll, minden két csúcs között p valószínűséggel él. Csúcsok növelésével exponenciálisan nő a kapcsolatszám. Kisvilág tulajdonság, ha összefüggő. Szinte mindig összefüggő, az óriáskomponens gyorsan kialakul, <math>p \sim \frac{1}{N} + \epsilon</math> |
==Barabássy-Albert gráf== | ==Barabássy-Albert gráf== | ||
A lap 2011. június 8., 15:20-kori változata
Rengeteg mindent fel lehet írni gráf alakban: internetes honlapok, szociális hálók, metabolikus folyamatok, szerzőségi hálók, tápláléklánc, körfolyamatok a fizikában és a biológiában, linux kernel stb.
Tartalomjegyzék
Alapfogalmak
- Egy gráf csúcsokból és élekből áll (lehet egy vagy több él két csúcs között, lehet a gráf irányított/irányítatlan, súlyozott/súlyozatlan).
- Gráf reprezentációja: mutatókkal, él-listákkal, vagy összekötöttségi mátrixokkal.
- Csúcs fokszáma: ahány él csatlakozik (fut be, vagy megy ki) a csúcshoz.
- Fokszám-eloszlás: egy gráf teljes fokszám-gyakoriság diagramja.
Kisvilág tulajdonság
Legyen a gráf összes csúcsának száma N. Két tetszőleges csúcs közötti legrövidebb út: legkevesebb csúcs érintésével. Legrövidebb utak átlagos hossza: l.
Kisvilág tulajdonság: 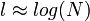
Erdős-Rényi gráf
N csúcsból áll, minden két csúcs között p valószínűséggel él. Csúcsok növelésével exponenciálisan nő a kapcsolatszám. Kisvilág tulajdonság, ha összefüggő. Szinte mindig összefüggő, az óriáskomponens gyorsan kialakul, 