Csega/Bolometry
A bolométer[1] egy, a beérkező elektromágneses sugárzás teljesítményének mérésére szolgáló eszköz. A teljesítmény mérése egy hőmérsékletfüggő ellenállással bíró anyag melegítésével történik, aminek hőmérsékletét a bejövő elektromágneses sugárzás emeli meg.
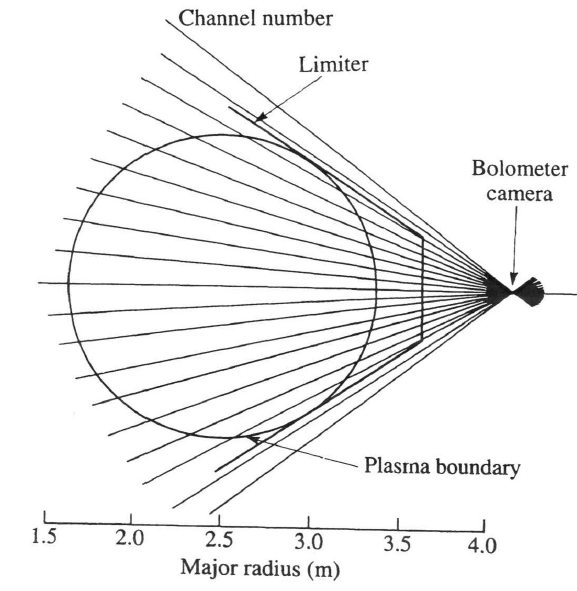
A plazmafizikában általában több bolométert helyeznek el pinhole kamera konfigurációban[2], így például a plazma egy bizonyos keresztmetszeti szeletét tudják monitorozni. A teljes keresztmetszeten a sugárzási teljesítmény kiszámításához ezeket az értékeket a teljes "kameraképre" föl kell integrálni. Ha a teljesítménynek a térbeli eloszlását is meg kell állapítani, akkor a mért adatokon végre kell hajtani egy Ábel-, vagy valamilyen más inverziót[3].
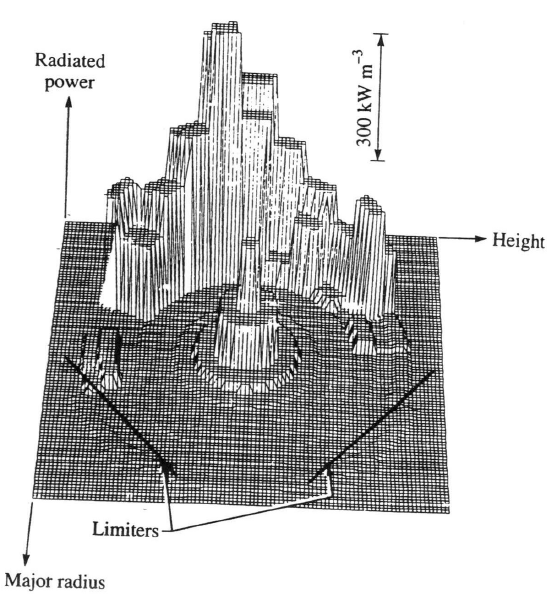
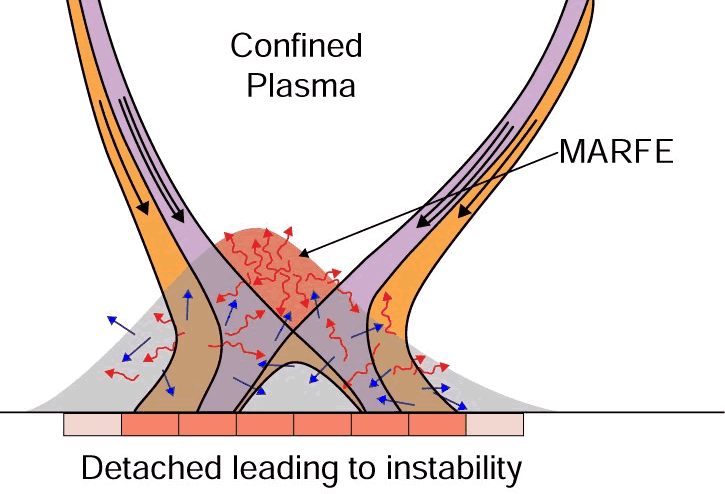
A fenti ábra poloidális aszimmetriát mutat a plazma belső felénél, ahol sokkal nagyobb a sugárzási teljesítmény, mint a többi résznél, méghozzá egy MARFE (Multi-faceted Asymmetric Radiation From the Edge - Sokrétű aszimmetrikus sugárzás a plazma széléről) miatt. A MARFE-ről ábra[4] alább látható:
A sugárzási teljesítményben felléphet toroidális aszimmetria is például a plazma limiterrel történő preferenciális kölcsönhatása miatt (ez nehezíti a mérések értelmezését). A detektorok általában lassú válaszidejűek és a semleges részecskefluxusra is érzékenyek.
<<<Vissza Csega plazmafizika lapjára
Hivatkozások
- ↑ See, for example, bolometers - Definition from the Merriam-Webster Online Dictionary
- ↑ Wesson - Tokamaks (3. kiadás, 541. oldal, a 2. kiadásban ugyanez az 511. oldalon található)
- ↑ Ábel inverzió (Jaffe - 1991.)
- ↑ Az EFDA honlapjáról (jobb oldalon egy pici ábra)