Atom- és molekulafizika

Az atom- és molekulafizika előadás és gyakorlat oldala

A tárgyhoz kapcsolódó dokumentumok

Vetített diák 1.

Vetített diák 2.

Gyakorlati összefoglaló

A alapállapoti energia szintek számolása

Az atomok energiaszintjeit a Schrödinger-egyeneltből számoljuk:

$H\Phi = E\Phi \,$

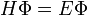
A Hidrogén-szerű egyrészecske Hamilton operátorban kinetikus enrgia szerepel és Coulomb-potenciál:

$H = -\frac{\hbar^2}{2m} \Delta -\frac{Ze_0^2}{r_0} \,$

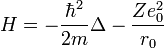
ahol Z a rendszám, 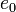$e_0$ a redukált töltés, m a redukált tömeg, közelítőleg az elektron tömege, Z a mag rendszáma. Az alapállapoti energia sajátértékek:

$E_{nlm} = -\frac{1}{2}\frac{Z^2 e_0^2}{a_0}\frac{1}{n^2}$

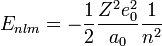
ahol n a főkvantumszám, értéke 0, 1, 2, ..., l a mellékkvantumszám, értéke 0-tól (n-1)-ig lehetséges, egyesével, és m a mágneses kvantunmszám, értéke (-l)-től (+l)-ig lehetséges egyesével.

A hullámfüggvényt sugár- és szögfüggő tényezőkre szeparálhatjuk:

$\Phi_{nlm}(\mathbf{r}) = R_{nl}(r) \cdot Y_l^m(\theta, \phi)$

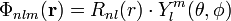
Többelektornos rendszerek

A alapállapoti perturbálatlan eset

A több elektront tartalmazó atomok elektronszerkezetét elsőrendű perturbációs módszerrel kezeljük, ahol az elektronok kölcsönhatása adja a perturbációs Hamilton operátort. He atomra:

$H = H_0 + H_1 = H_0 + \frac{e_0^2}{r_{12}}$

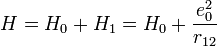
A többrészecskés esetben a perturbálatlan Hamilton(He atomra N=2):

$H_0 = \sum_{i=1}^{N} -\frac{\hbar^2}{2m_i} \Delta_i -\frac{Ze_0^2}{r_i}$

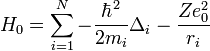
Az alapállapoti hullámfüggvényt kereshetjük ismét szorzat alakban, azonban vegyük figyelembe a spint is:

$\Psi_0 = \Phi_{100}(\mathbf{r_1}) \cdot \Phi_{100}(\mathbf{r_2}) \cdot \chi( s_1, s_2 )$

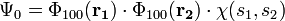
Alapállapotban ez megtehető, mert a spintényező antiszimmetrikus, a hely- és szögfüggő rész szimmetrikus (ez kötelező alapállapotban), így az eredő hullámfüggvény antiszimmetrikus összhangban a Pauli-elvvel. Továbbá, mivel a tekintett Hamilton-operátor nem függ a spintől, ezért a számolások során ez mindig kihozható az integrálok alól, és a skaláris szorzat számolása során az ortonormalitás miatt 1-et ad.

Az alapállapoti energia ekkor:

$E_0 = \langle\Psi_0|H|\Psi_0\rangle = \langle\Psi_0|H_0|\Psi_0\rangle + \langle\Psi_0|H_1|\Psi_0\rangle = E_0^0 + E_0^1 \,$

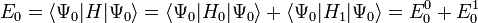
Az első tag a két Hidrogén-szerű alapállapot (n=1) energiasajátértékének összege, ezért:

$E_0^0 = 2 \cdot -\frac{1}{2}\frac{Z^2 e_0^2}{a_0}$

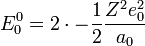
A alapállapoti perturáció

Az elektron-elektron kölcsönhatási perturbáció számolása:

$E_0^1 = \langle\Psi_0|H_1|\Psi_0\rangle = \int d^3 r_1 \int d^3 r_2 \Phi_{100}(\mathbf{r_1})^* \Phi_{100}(\mathbf{r_2})^* \frac{e_0^2}{r_{12}} \Phi_{100}(\mathbf{r_1}) \Phi_{100}(\mathbf{r_2})$

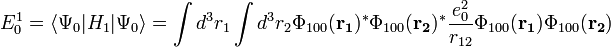
ahol a spint már kiösszegeztük. A további lépések:

• Beírjuk a szorzat alakú hullámfüggvényt.
• A 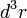$d^3 r$ integrálási változók helyett gömbi koordinátákra térünk át: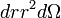 $dr r^2 d\Omega\,$
• Beírjuk 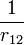$\frac{1}{r_{12}}$ helyére a gömbfüggvények szerinti összegképletet. Ebben a kifejtésben a gömbfüggvények különböző argumentummal szerepelnek a szumma alatt, ezért beviszünk mindkettőhöz 1-1 hozzátartozó argumentumú gömbfüggvényt a hullámfüggvényekből, és a szumma alatt kiintegráljuk, ami az ortonormalitás miatt Kronecker-deltákat eredményez, így a szummák elvégezhetőek, és l konkrét értéket vesz fel. A kint maradt gömbfüggvények m=0,l=0 értékekhez tartoznak, azaz értékük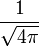 $\frac{1}{\sqrt{4\pi}}$
• Ekkor már csak a sugár függő integrálok maradnak, amelyek 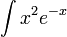$\int x^2 e^{-x}$ alakúak, és analitikusan kiszámolhatóak.

Hélium-szerű gerjesztett állapotok

A kételektron rendszereknek azon gerjesztéseit tekintjük, amelyeknél csak az egyik elektron van az alapállapotnál magasabban, a másik alapállapotban:

$\Psi_a(1) = \Phi_{100}(\mathbf{r_1})$

$\Psi_b(2) = \Phi_{2lm}(\mathbf{r_2})$

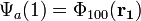
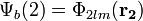
Ez azért jogos, mert ha mindkettő magasabb szinten lenne, az már nem lenne kötött állapot. Ekkor már tlejesíthető a Pauli-elv két féle kombináció esetén: szimmetrikus a helyfüggvény és antiszimmetrikus a spin függvény VAGY antiszimmetrikus a helyfüggvény és szimmetrikus a spin függvény.

A hullámfüggvény alakja tehát szimmetrikus esetben: $\Psi_{0, szimm} = \frac{1}{\sqrt{2}}\left(\Phi_a(1)\Phi_b(2) - \Phi_a(2)\Phi_b(1) \right) \cdot ^3\chi(s_1, s_2)$

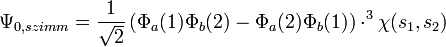
A hullámfüggvény alakja antiszimmetrikus esetben: $\Psi_{0, antiszimm} = \frac{1}{\sqrt{2}}\left(\Phi_a(1)\Phi_b(2) + \Phi_a(2)\Phi_b(1) \right) \cdot ^1\chi(s_1, s_2)$

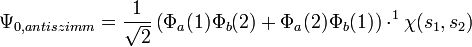
A szimmetrikus esetben három különböző spinfüggvény létezik, ezért három féle 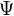$\Psi$ állítható elő, ezért ez az állapot triplett, az antiszimmetrikus esetben csak egy létezik, ezért ez szinglett.

A perturbálatlan eset

A perturbálatlan eset most is a Hidrogén-szerű energiaértékekből számolható:

$E_1^0 = E_{100} + E_{200} = -\frac{Z^2 e_0^2}{2a_0}\left( \frac{1}{1^2} + \frac{1}{2^2} \right)$

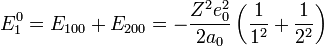
A perturbált eset

A főbb lépések:

• A spin ismét kiösszegezhető, és 1-et ad.
• Az hullámfüggvényben levő összeget (vagy különbséget) felbontjuk négy tagra a skalárszorzatban. Ebből a vegyes tagok azonosak egy változó csere erejéig, ezért összevonhatóak, hasonlóan a négyzetes tagok is, így két integrált kapunk: egy Kicserélődési és egy Coulomb integrált:

$C_{ab} = e_0^2 \int d^3 r_1 \int d^3 r_2 \frac{|\Phi_{a1}|^2 |\Phi_{b2}|^2}{r_{12}}$

$K_{ab} = e_0^2 \int d^3 r_1 \int d^3 r_2 \frac{\Phi_{a1}^* \Phi_{b1} \Phi_{b2}^* \Phi_{a2}}{r_{12}}$

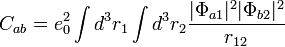
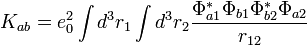
• Beírjuk a szorzat alakú hullámfüggvényt.
• A 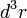$d^3 r$ integrálási változók helyett gömbi koordinátákra térünk át: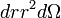 $dr r^2 d\Omega\,$
• Beírjuk 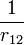$\frac{1}{r_{12}}$ helyére a gömbfüggvények szerinti összegképletet. Bevisszük az integrálokat a szumma alá, és csoportosítjuk az azonos argumentumú gömbfüggvényeket. Ezeket vagy a norma, vagy az ortogonalitás segítségével elvégezzük. Az összegző kvantumsázmok értéke meghatározódik, és helyükbe a meghatározandó gerjesztett pálya kvantumszámai írhatóak.
• A hátramaradó integrálok 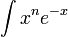$\int x^n e^{-x}$ alakúak, és elvégezhetőek.