VélFiz 7.tétel

7.tétel: Hálózatok fokszámeloszlásának leírása

Barabási-Albert hálózat

(Akinek ez túl bonyolult, az megtanulhatja az Random-Rekurzív hálót is - persze az lehet, hogy vmivel rosszabb jegyet jelent...)

Ebben az esetben általában adott egy kezdeti hálózat, adott élekkel. A gráfot minden lépésben eggyel növeljük. Az új csúcs éle a többiek fokszámától fog függeni: minél nagyobb egy csúcs fokszáma, annál nagyobb valószínűséggel fog ahhoz csatlakozni. Ha ez utóbbi r valószínűséget jelent, akkor 1-r valószínűséggel fog csatlakozni véletlenszerűen egy másik csúcshoz.

$w_{k} \sim k^{\gamma}$

$k^{\gamma} \sim A_{k}$

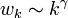
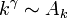
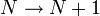$N\rightarrow N+1$ adja az időlépést (az idő telését az új csúcs érkezésének feleltettük meg)

(Ide kellene egy kis jelmagyarázat, h pontosan miket is jelentenek az egyes betűk - ellég rosszul jegyzeteltem itt, sry. Cz)

Speciális esetek:

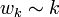• $w_{k} \sim k$ -> Lineáris preferencia
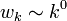• $w_{k} \sim k^{0}$ -> Véletlen fa gráf

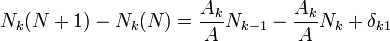$N_{k}(N+1)-N_{k}(N)=\frac{A_{k}}{A}N_{k-1}-\frac{A_{k}}{A}N_{k}+\delta_{k1}$, ahol A egy normalizációs faktor: $A=\sum_{j}j^{\gamma}N_{j}$