Kanonikus formalizmus

A Hamilton-egyenletek

A Lagrange-formalizmussal szemben, amely a klasszikus fizika általános koordináták és sebességek szerinti megfogalmazása, a Hamilton-formalizmusnál a rendszer leírásához az általános koordinátákat és impulzusokat használjuk. Ez különösen pl. a mechanika általános kérdéseinek vizsgálatában előnyös. Az alapegyenleteket a Hamilton-függvény segítségével fogalmazzuk meg, amely definíció szerint a Lagrange-függvény Legendre-transzformáltja:

$H(p,q,t) = \sum{\dot{p_i} q_i} - L$

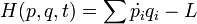
ahol 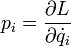$p_i = \frac{\partial{L}}{\partial{\dot{q_i}}}$ az általános impulzusokat jelöli. Az alapegyenletek levezetéséhez a Lagrange-függvény teljes differenciálja:

$dL = \sum\frac{\partial{L}}{\partial{q_i}} dq_i + \sum\frac{\partial{L}}{\partial{\dot{q_i}}} \dot{dq_i} = \sum \dot{p_i} dq_i + \sum p_i \dot{dq_i}$

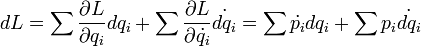
ahol kihasználtuk a Lagrange-egyenletet. Ennek a második tagját

$\sum p_i \dot{dq_i} = d(\sum p_i \dot{q_i}) - \sum \dot{q_i} dp_i$

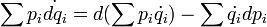
alakban írva:

$d(\sum p_i \dot{q_i} - L) = - \sum{\dot{p_i}dq_i}+\sum{\dot{q_i}dp_i}$

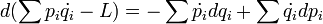
Amiből már leolvashatók a Hamilton-egyenletek, a kanonikus formalizmus alapegyenletei:

$\dot{q_i}=\frac{\partial{H}}{\partial{p_i}}$

$\dot{p_i}=-\frac{\partial{H}}{\partial{q_i}}$

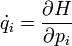
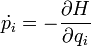
A Hamilton-függvény

A Hamilton-függvény nem más, mint az anyagi rendszer energiája (lásd: Megmaradási tételek). A teljes időderiváltja:

$\frac{dH}{dt} = \frac{\partial{H}}{\partial{t}} + \sum{\frac{\partial{H}}{\partial{q_i}}}\dot{q_i} + \sum{\frac{\partial{H}}{\partial{p_i}}}\dot{p_i} = \frac{\partial{H}}{\partial{t}}$

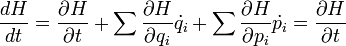
ahol kihasználtuk a Hamilton-egyenleteket. Ha a Hamilton-függvény expliciten nem függ az időtől akkor ez az energiamegmaradást adja. Ha a Lagrange- és a Hamilton-függvények valamilyen 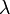$\lambda$ paramétertől függnek:

$\frac{\partial{H}}{\partial{\lambda}}=-\frac{\partial{L}}{\partial{\lambda}}$

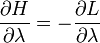
ami a teljes derivált felírásából látható. Speciálisan amikor 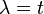$\lambda = t$, akkor is igaz.