A statisztikus fizika matematikai apparátusa

Stirling-formula

Nagy n esetén közelítőleg:

$n! \sim \sqrt{2 \pi n} \left( \frac{n}{e} \right)^n$

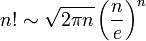
Az előző állítás pontosabb megfogalmazása az, hogy a két oldal aszimptotikusan egyenlő, vagyis a hányadosuk végtelenben vett határértéke 1. Általában a formulát a következőképpen használjuk ki:

$\ln(n!) \sim n \cdot (\ln(n) - 1)$

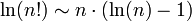
Néhány integrál

Gauss-integrál (precízen az alábbi formula a = 1 esetét nevezik Gauss-integrálnak):

$\int\limits_{-\infty}^\infty e^{-ax^2}dx = \sqrt{\frac{\pi}{a}}$

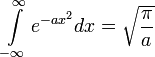
Gamma-függvény:

$\int\limits_{0}^\infty t^{z-1} e^t dt = \Gamma(z)$

$\Gamma\left(\frac{1}{2}\right) = \pi^{\frac{1}{2}}$

$\Gamma(x+1) = x\, \Gamma(x)$

$\Gamma(n) = \,(n-1)!$

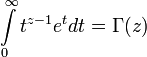
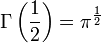
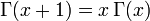
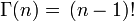
Egy r sugarú, d dimenziós gömb térfogata:

$V = \frac{\pi^{d/2}}{\Gamma(1+d/2)}r^d$

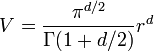
A Bose-Einstein kondenzációhoz kell a következő integrál:

$\int\limits_{0}^\infty x^{\frac{1}{2}} \frac{1}{e^x-1} dx = \Gamma\left(\frac{3}{2}\right) \zeta\left(\frac{3}{2}\right)$

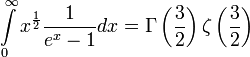
Ehhez hasonló integrálok gyakran bukkannak elő a statisztikus fizikában és a szilárdtest fizikában, általános alakjuk:

$\int\limits_{0}^{\infty}\frac{x^{n}}{e^x-1}\,dx = \Gamma{\left(n+1\right)} \zeta(n+1)$

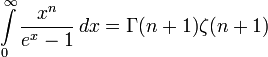
ahol 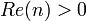$Re(n) > 0$, illetve

$\int\limits_{0}^{\infty}\frac{x^{n}}{e^x+1}\,dx = \Gamma{\left(n+1\right)} \zeta(n+1) (1-2^{-n})$

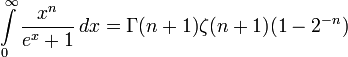
ahol 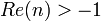$Re(n) > -1$.

Ami, mint könnyen látható, a Fermi-Dirac statisztikával kapcsolatos számításokban bukkan fel gyakran.

Sorfejtések

Magas hőmérsékletű kvantumkorrekciók

... Ezt a részt majd átrakom máshova...

A 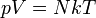$pV = NkT$ ideális gázegyenlet első kvantumkorrekcióját keressük, a közelítés: 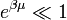$e^{\beta \mu} \ll 1$. Ehhez a következő sorfejtést használjuk:

$\frac{1}{e^{\beta (\epsilon - \mu)} \pm 1} = e^{-\beta (\epsilon - \mu)} \sum\limits_{0}^{\infty} (\mp)^l e^{-l \beta (\epsilon - \mu)} \approx e^{-\beta (\epsilon - \mu)} \mp e^{-2\beta (\epsilon - \mu)}$

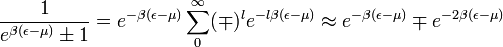
Bethe-Sommerfeld sorfejtés

Fermionokra használható alacsony hőmérsékleten.