A relativitáselmélet matematikai alapjai
Tartalomjegyzék
Sajátidő
A relativitáselmélet egyik elsőre szokatlannak tűnő következménye az idő relativitása, az, hogy az idő az egymáshoz képest mozgó koordinátarendszerekben nem ugyanúgy telik. Az álló koordinátarendben levő megfigyelőhöz képest (fénysebességgel összemérhető sebességgel) mozgó rendszerben az idő lassabban telik. Érdemes kiszámolni egy a téridő általános görbéje mentén mozgó részecske számára eltelt időt (azt az időt, amit a részecskével együtt mozgó óra mérne). Ha a részecske mozgása nem egyenletes, akkor a hozzá rögzített koordinátarendszer nem inerciarendszer, de minden pillanatban választható egy pillanatnyi inerciarendszer, aminek a sebessége pont megegyezik a részecske sebességével. Egy általános inerciarendszerben (legyen ez a megfigyelő koordinátarendszere) fel lehet írni (egy 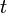 pillanatban) a részecske pályáján számított infinitezimális ívhosszat:
pillanatban) a részecske pályáján számított infinitezimális ívhosszat: 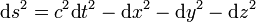 Ez az ívelemnégyzet megegyezik a pillanatnyi inerciarendszerben felírt ívelemnégyzettel. A pillanatnyi inerciarendszerben a részecske áll, így itt
Ez az ívelemnégyzet megegyezik a pillanatnyi inerciarendszerben felírt ívelemnégyzettel. A pillanatnyi inerciarendszerben a részecske áll, így itt 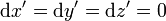 , csak az idő telik, így:
, csak az idő telik, így: 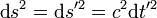 . Ebből kifejezhető a részecske pillanatnyi inerciarendszerében vett infinitezimális időtartam:
. Ebből kifejezhető a részecske pillanatnyi inerciarendszerében vett infinitezimális időtartam:
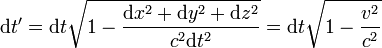
Itt 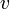 a részecske sebessége a megfigyelő inerciarendszeréhez képest, a
a részecske sebessége a megfigyelő inerciarendszeréhez képest, a 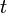 időpontban. Ha adott a részecske pályája a megfigyelő rendszerében (a megfigyelő rendszerében eltelő idő függvényében), akkor az előző egyenletet integrálva megkaphatjuk, hogy mennyi
időpontban. Ha adott a részecske pályája a megfigyelő rendszerében (a megfigyelő rendszerében eltelő idő függvényében), akkor az előző egyenletet integrálva megkaphatjuk, hogy mennyi  idő telik el a részecskével együtt mozgó rendszerben a megfigyelő rendszerében eltelt
idő telik el a részecskével együtt mozgó rendszerben a megfigyelő rendszerében eltelt 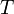 idő alatt:
idő alatt:
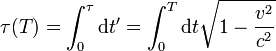
Az első integrál a mozgó rendszerben van felírva, ezt írtuk át a megfigyelő rendszerében elvégezhető integrállá, 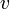 a részecske pillanatnyi sebessége a megfigyelő rendszerében. A gyökös kifejezés értéke mindig kisebb, mint
a részecske pillanatnyi sebessége a megfigyelő rendszerében. A gyökös kifejezés értéke mindig kisebb, mint 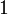 , így láthatóan a mozgó rendszerben eltelő idő rövidebb:
, így láthatóan a mozgó rendszerben eltelő idő rövidebb: 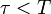 .
Az első integrál mindig a pillanatnyi inerciarendszerekben értendő (amikhez képest a részecske áll), így
.
Az első integrál mindig a pillanatnyi inerciarendszerekben értendő (amikhez képest a részecske áll), így 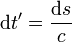 , így a kiszámolt
, így a kiszámolt  mennyiség a téridőbeli görbe ívhosszával arányos. A
mennyiség a téridőbeli görbe ívhosszával arányos. A  mennyiséget a részecske sajátidejének nevezzük, és értéke bármely inerciarendszerből számolva ugyanaz (az ívhossz invariáns), így jól alkalmazható a téridőbeli görbék paraméterezésére.
mennyiséget a részecske sajátidejének nevezzük, és értéke bármely inerciarendszerből számolva ugyanaz (az ívhossz invariáns), így jól alkalmazható a téridőbeli görbék paraméterezésére.
4-es formalizmus, kinematika
A helyvektor
A téridőben egy pontot egy valamely inerciarendszerhez viszonyított 4 (egy idő- és 3 tér-) koordinátával lehet meghatározni. Érdemes ezeket egy 4 komponensű vektorba foglalni: 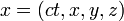 . A vektor komponenseit jelölő indexet ebben az esetben fentre szokás tenni, és a számozás 0-tól indul. Így:
. A vektor komponenseit jelölő indexet ebben az esetben fentre szokás tenni, és a számozás 0-tól indul. Így: 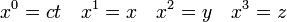 . Az indexeket általánosan görög betűkkel szokás jelölni (egy egyenletben
. Az indexeket általánosan görög betűkkel szokás jelölni (egy egyenletben 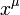 jelölheti az
jelölheti az 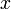 4-esvektor bármelyik komponensét;
4-esvektor bármelyik komponensét; 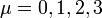 )
)
Áttérve egy másik koordinátarendszerbe egy Lorentz-transzformációt kell elvégeznünk. A transzformáció kifejezhető a fenti vektor egy mátrixxal szorzásával: 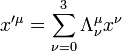 , ahol
, ahol 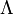 a Lorentz-transzformáció mátrixa (az összegzőindexe alul van). A továbbiakban az ehhez hasonló képletekből a
a Lorentz-transzformáció mátrixa (az összegzőindexe alul van). A továbbiakban az ehhez hasonló képletekből a 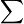 jelet elhagyjuk (ahogy az az irodalomban megszokott), a kétszer (egy alul és egy felül) előforduló indexekre automatikus összegzés értendő. A Lorentz-transzformáció mátrixa például
jelet elhagyjuk (ahogy az az irodalomban megszokott), a kétszer (egy alul és egy felül) előforduló indexekre automatikus összegzés értendő. A Lorentz-transzformáció mátrixa például  irányú boost esetén:
irányú boost esetén:
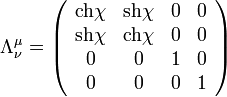
Alsó indexes vektorok, abszolút érték
Az alsó indexes vektorok bevezetése a metrikus tenzor segítségével történhet, ami a speciális relativitáselméletben:
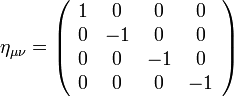
Megjegyezzük, hogy a metrikus tenzor 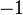 -szerese is jó választás lenne, az irodalomban mindkettő előfordul, egy relativitáselmélettel foglalkozó számolás elején érdemes leszögezni, hogy az ember éppen melyik konvenciót használja. Az alsó indexes vektorokat az
-szerese is jó választás lenne, az irodalomban mindkettő előfordul, egy relativitáselmélettel foglalkozó számolás elején érdemes leszögezni, hogy az ember éppen melyik konvenciót használja. Az alsó indexes vektorokat az 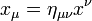 képlettel definiáljuk (itt is természetesen
képlettel definiáljuk (itt is természetesen 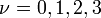 -ra összegzés értendő), így
-ra összegzés értendő), így 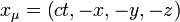 . A metrikus tenzorral szorzást az indexek lehúzásának nevezzük. Az egyenletekben általános szabály, hogy egy indexnek mindkét oldalon ugyanott (vagy alul, vagy felül) kell szerepelnie. Természetesen az indexek lehúzása invertálható, az alsó indexes vektorokból a
. A metrikus tenzorral szorzást az indexek lehúzásának nevezzük. Az egyenletekben általános szabály, hogy egy indexnek mindkét oldalon ugyanott (vagy alul, vagy felül) kell szerepelnie. Természetesen az indexek lehúzása invertálható, az alsó indexes vektorokból a 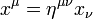 összefüggéssel kaphatunk felső indexeseket, ahol az
összefüggéssel kaphatunk felső indexeseket, ahol az 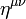 az alsó indexessel numerikusan megegyező mátrix, algebrai értelemben azonban az inverze, az alsó és felső indexes
az alsó indexessel numerikusan megegyező mátrix, algebrai értelemben azonban az inverze, az alsó és felső indexes 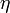 -kat összeszorozva a
-kat összeszorozva a 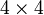 -es egységmátrixot kapjuk:
-es egységmátrixot kapjuk:
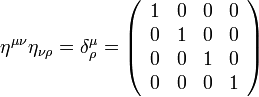
Ha egy alsó indexes vektort akarunk transzformálni, ahhoz a Lorentz-mátrix indexeit is le- illetve fel kell húznunk, ami a vektorindexekhez hasonlóan tehető meg.
Egy 4-esvektor abszolútértéknégyzetén az 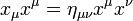 szorzatot értjük. Ennek a lényege az, hogy ilyen definíciókkal számolva egy infinitezimális elmozdulásvektor abszolútértéknégyzete éppen az ívelemnégyzetet adja:
szorzatot értjük. Ennek a lényege az, hogy ilyen definíciókkal számolva egy infinitezimális elmozdulásvektor abszolútértéknégyzete éppen az ívelemnégyzetet adja:
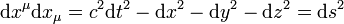
Általános 4-es tenzorok
Természetesen nem csak a koordináták, illetve a különbségeik alkotnak 4-esvektort, hanem mindazok a fizikai 4-es mennyiségek, amik egy másik inerciarendszerbe áttérve a koordinátákhoz hasonlóan (a megfelelő Lorentz-transzformációs mátrixszal) transzformálódnak. Ilyenek például az elektrodinamikában a potenciálok (az elektrosztatikus potenciál és a vektorpotenciál 3 komponense).
Be lehet vezetni a többindexes 4-estenzorokat is, ezeknek az a definíciója, hogy a másik koordinátarendszerbe áttérve mindegyik indexük a 4-esvektorokhoz hasonlóan transzformálódik:
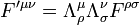
Az elektrodinamikában például az elektromos és mágneses térerősségek komponenseiből lehet egy 4-es tenzort alkotni.
A fizikai egyenletekre való követelmény az, hogy mindkét oldalon ugyanúgy transzformálódó mennyiségek legyenek.