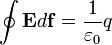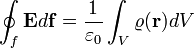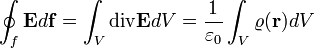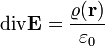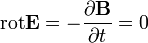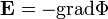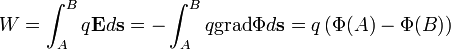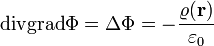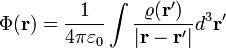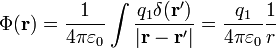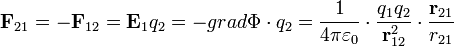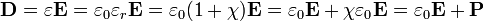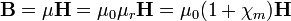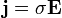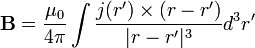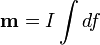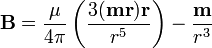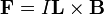„Elektro- és magnetosztatika, áramkörök” változatai közötti eltérés
a |
Rudi (vitalap | szerkesztései) (→Coulomb- és Gauss-törvény, szuperpozíció elve, stacionárius áram.Feynman - Mai Fizika 5: 56. Elektrosztatika) |
||
| 1. sor: | 1. sor: | ||
| − | ==Coulomb- és Gauss-törvény, szuperpozíció elve, stacionárius áram. | + | ==Coulomb- és Gauss-törvény, szuperpozíció elve, stacionárius áram.== |
| − | + | ===ELektrosztatika=== | |
| − | <math>\ | + | '''Sztatika''' esetén nincsen időbeli változás, tehát a Maxwell-egyenletekben <ref>Teljes Maxwell-egyenletek: [[Elektrodinamika|itt]]</ref> szereplő, időderiváltakat tartalmazó targok 0-t adnak járulákul. Így a Mexwell-egyenletek: (ahol <math>\mathbf{E}</math> az elektromos térerősség, <math>\mathbf{B}</math> a mágneses indukció, <math>\mathbf{j}</math> az áramsűrűség, <math>\varrho</math> az elektromos töltéssűrűség, <math>\varepsilon_{0}</math> a vákuum dielektromos állandója) |
| − | <math>\operatorname{ | + | <math>\operatorname{div}\mathbf{E}=\frac{\varrho}{\varepsilon_{0}}</math> |
| − | <math>\operatorname{rot} | + | <math>\operatorname{rot}\mathbf{E}=0</math> |
| − | <math>\operatorname{ | + | <math>\operatorname{rot}\mathbf{B}=\frac{\mathbf{j}}{\varepsilon_{0}c^{2}}</math> |
| − | + | <math>\operatorname{div}\mathbf{B}=0</math> | |
| − | |||
| − | + | ====Gauss-törvény==== | |
| − | + | Gauss-törvénynek az első Maxwell-egyenletet nevezzük. Az elektromos töltések, vagy töltéseloszlás, és az elektromos tér kapcsolatát adja meg. Integrális formában azt mondja ki, hogy ha egy <math>q</math> töltést körbeveszünk egy zárt felülettel, akkor arra integrálva az elektromos teret (<math>\mathbf{E}</math>), a töltéssel arányos mennyiséget kapunk: | |
| − | + | :<math> | |
| + | \oint \mathbf{E} d\mathbf{f} = \frac{1}{\varepsilon_0}q | ||
| + | </math> | ||
| − | + | Ahol <math>\varepsilon_0</math>, az arányossági tényező reciproka, a vákuum dielektromos állandója. Általánosabban felírhatjuk töltéseloszlásra is, aminek alesete több ponttöltés: | |
| − | + | :<math> | |
| + | \oint_f \mathbf{E} d\mathbf{f} = \frac{1}{\varepsilon_0} \int_V \varrho(\mathbf{r}) dV | ||
| + | </math> | ||
| − | + | Ezt nevezzük a '''Gauss-törvény integrális formájának'''. <math>\varrho(\mathbf{r})</math> a töltéssűrűség, <math>V</math> pedig az <math>f</math> zárt felület által határolt térfogat. A matematikai Gauss-törvény értelmében egy vektortér divergenciájának térfogatra vett integrálja egyenlő a vektortér határfelületre vett integráljával, vagyis: | |
| − | + | :<math> | |
| + | \oint_f \mathbf{E} d\mathbf{f} = \int_V \operatorname{div} \mathbf{E} dV = \frac{1}{\varepsilon_0} \int_V \varrho(\mathbf{r}) dV | ||
| + | </math> | ||
| − | : | + | Mivel az egyenlet két oldalán ugyanarra a térfogyatra integrálunk, az integrandusok is egyenlőek: |
| − | + | :<math> | |
| + | \operatorname{div} \mathbf{E} = \frac{\varrho(\mathbf{r})}{\varepsilon_0} | ||
| + | </math> | ||
| − | + | Ez a '''Gauss-törvény differenciális formája'''. | |
| − | |||
| − | + | ====Coulomb-törvény==== | |
| − | + | Elektrosztatikában minden időderivált eltűnik: <math>\frac{\partial}{\partial t} \equiv 0</math>. Így a Faraday-törvény (egy másik Maxwell-egyenlet) így alakul: | |
| − | <math>\ | + | :<math>\operatorname{rot} \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t} = 0</math> |
| − | + | Rotációmentes vektorterek előállíthatóak egy skalárfüggvény gradienseként, ezért vezessük be a <math>\Phi</math> skalárpotenciált, amelyre igaz: | |
| − | + | :<math> | |
| + | \mathbf{E} = - \operatorname{grad} \Phi | ||
| + | </math> | ||
| − | + | <math>\Phi</math> skalárpotenciál dimenziója energia/töltés, így adott töltés esetén arányos a potenciális energiával, és egy <math>q</math> töltést mozgatva elektromos térben <math>A</math> pontból <math>B</math> pontba, megadja a végzett <math>W</math> munkát: | |
| − | + | :<math>W = \int_A^B q \mathbf{E} d\mathbf{s} = - \int_A^B q \operatorname{grad} \Phi d\mathbf{s} = q \left(\Phi(A) - \Phi(B)\right)</math> | |
| − | + | A gradienses egyenletet beírva a divergenciásba, kapjuk a Poisson-egyenletet: | |
| − | + | :<math> | |
| + | \operatorname{div} \operatorname{grad} \Phi = \Delta \Phi = - \frac{\varrho(\mathbf{r})}{\varepsilon_0} | ||
| + | </math> | ||
| + | |||
| + | A levezetést mellőzve, Green-módszerrel megoldható az egyenlet, az általános megoldás pedig: | ||
| + | |||
| + | :<math>\Phi (\mathbf{r}) = \frac{1}{4 \pi \varepsilon_0} \int \frac{\varrho(\mathbf{r}')}{|\mathbf{r} - \mathbf{r}'|} d^3\mathbf{r}'</math> | ||
| + | |||
| + | Ha az Origóban van egyetlen, <math>q_1</math> töltésű ponttöltésünk, akkor <math>\varrho(\mathbf{r}) = q_1\delta(\mathbf{r})</math>. Erre könnyen el lehet végezni az integrált: | ||
| + | |||
| + | :<math>\Phi (\mathbf{r}) = \frac{1}{4 \pi \varepsilon_0} \int \frac{q_1\delta(\mathbf{r}')}{|\mathbf{r} - \mathbf{r}'|}=\frac{q_1}{4 \pi \varepsilon_0} \frac{1}{r}</math> | ||
| + | |||
| + | Az ebbe a térbe helyezett <math>q_2</math> töltésre ható erő: | ||
| + | |||
| + | :<math> | ||
| + | \mathbf{F}_{21} = - \mathbf{F}_{12} = \mathbf{E}_1q_2 = -grad \Phi \cdot q_2 = \frac{1}{4 \pi \varepsilon_0} \cdot \frac{q_1q_2}{\mathbf{r}_{12}^2} \cdot \frac{\mathbf{r}_{21}}{r_{21}} | ||
| + | </math> | ||
| + | |||
| + | Ezt nevezzük '''Coulomb-törvénynek'''. | ||
| + | |||
| + | A Maxwell-egyenletek linearitása miatt egy adott pontban különböző töltések által keltett elektromos tér értéke megegyezik az egyéni töltések által létrehozott terek vektoriális összegével. Belátható, hogy ez egyenértékű azzal, hogy az egyes töltések által létrehozott skalárpotenciálok is összeadódnak. Ezt nevezzük a '''szuperpozíció elvének'''. | ||
==Vezetők, szigetelők, dielektrikumok, elektormos polarizáció, magnetosztatika.== | ==Vezetők, szigetelők, dielektrikumok, elektormos polarizáció, magnetosztatika.== | ||
A lap 2011. június 19., 15:19-kori változata
Tartalomjegyzék
Coulomb- és Gauss-törvény, szuperpozíció elve, stacionárius áram.
ELektrosztatika
Sztatika esetén nincsen időbeli változás, tehát a Maxwell-egyenletekben [1] szereplő, időderiváltakat tartalmazó targok 0-t adnak járulákul. Így a Mexwell-egyenletek: (ahol 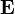 az elektromos térerősség,
az elektromos térerősség, 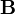 a mágneses indukció,
a mágneses indukció, 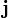 az áramsűrűség,
az áramsűrűség, 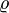 az elektromos töltéssűrűség,
az elektromos töltéssűrűség, 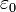 a vákuum dielektromos állandója)
a vákuum dielektromos állandója)
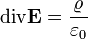
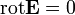
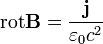
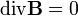
Gauss-törvény
Gauss-törvénynek az első Maxwell-egyenletet nevezzük. Az elektromos töltések, vagy töltéseloszlás, és az elektromos tér kapcsolatát adja meg. Integrális formában azt mondja ki, hogy ha egy 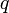 töltést körbeveszünk egy zárt felülettel, akkor arra integrálva az elektromos teret (
töltést körbeveszünk egy zárt felülettel, akkor arra integrálva az elektromos teret (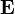 ), a töltéssel arányos mennyiséget kapunk:
), a töltéssel arányos mennyiséget kapunk:
Ahol 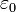 , az arányossági tényező reciproka, a vákuum dielektromos állandója. Általánosabban felírhatjuk töltéseloszlásra is, aminek alesete több ponttöltés:
, az arányossági tényező reciproka, a vákuum dielektromos állandója. Általánosabban felírhatjuk töltéseloszlásra is, aminek alesete több ponttöltés:
Ezt nevezzük a Gauss-törvény integrális formájának. 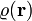 a töltéssűrűség,
a töltéssűrűség, 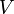 pedig az
pedig az 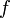 zárt felület által határolt térfogat. A matematikai Gauss-törvény értelmében egy vektortér divergenciájának térfogatra vett integrálja egyenlő a vektortér határfelületre vett integráljával, vagyis:
zárt felület által határolt térfogat. A matematikai Gauss-törvény értelmében egy vektortér divergenciájának térfogatra vett integrálja egyenlő a vektortér határfelületre vett integráljával, vagyis:
Mivel az egyenlet két oldalán ugyanarra a térfogyatra integrálunk, az integrandusok is egyenlőek:
Ez a Gauss-törvény differenciális formája.
Coulomb-törvény
Elektrosztatikában minden időderivált eltűnik: 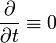 . Így a Faraday-törvény (egy másik Maxwell-egyenlet) így alakul:
. Így a Faraday-törvény (egy másik Maxwell-egyenlet) így alakul:
Rotációmentes vektorterek előállíthatóak egy skalárfüggvény gradienseként, ezért vezessük be a 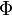 skalárpotenciált, amelyre igaz:
skalárpotenciált, amelyre igaz:
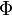 skalárpotenciál dimenziója energia/töltés, így adott töltés esetén arányos a potenciális energiával, és egy
skalárpotenciál dimenziója energia/töltés, így adott töltés esetén arányos a potenciális energiával, és egy 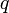 töltést mozgatva elektromos térben
töltést mozgatva elektromos térben 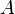 pontból
pontból 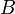 pontba, megadja a végzett
pontba, megadja a végzett 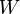 munkát:
munkát:
A gradienses egyenletet beírva a divergenciásba, kapjuk a Poisson-egyenletet:
A levezetést mellőzve, Green-módszerrel megoldható az egyenlet, az általános megoldás pedig:
Ha az Origóban van egyetlen, 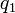 töltésű ponttöltésünk, akkor
töltésű ponttöltésünk, akkor 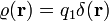 . Erre könnyen el lehet végezni az integrált:
. Erre könnyen el lehet végezni az integrált:
Az ebbe a térbe helyezett 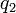 töltésre ható erő:
töltésre ható erő:
Ezt nevezzük Coulomb-törvénynek.
A Maxwell-egyenletek linearitása miatt egy adott pontban különböző töltések által keltett elektromos tér értéke megegyezik az egyéni töltések által létrehozott terek vektoriális összegével. Belátható, hogy ez egyenértékű azzal, hogy az egyes töltések által létrehozott skalárpotenciálok is összeadódnak. Ezt nevezzük a szuperpozíció elvének.
Vezetők, szigetelők, dielektrikumok, elektormos polarizáció, magnetosztatika.
Vezetők[2]
Az elektromos vezetők - általában fémek - belsejében a delokalizált elektronok áramlása hozza létre a vezetés jelenségét. Ezt okozhatja például külső elektromos erőtér. Az így létrehozott áramot vagy mozgásban kell tartani egy külső energiaforrással, különben amint az elektronok kisütik a kezdeti teret létrehozó forrásokat, megállnak. Tehát az elektronok addig mozognak, amíg úgy nem rendeződnek, hogy a belső elektromos tér nulla legyen. Mivel a tér belül zérus, így annak divergenciája is nulla, és a Gauss-törvény értelmében akkor a töltéssűrűségnek is 0-nak kell lennie. Tehát a töltéseknek a vezető felületén kell lenniük.
Továbbá a vezető felülete ekvipotenciális felület, a térerősségnek itt merőlegesnek kell lennie mindenhol. Ha lenne érintőleges tag, akkor az elektronok elmozdulnának a felület mentén.
Végül bebizonyítható, hogy a vezető belsejében levő (üres) üregben a térerősség szintén zérus.
Dielektrikumok[3]
A dielektrikumok (vagy szigetelők) nem vezetik az áramot, visznont van elektromos tulajdonságuk (pl kondenzátor kapacitása megnő, ha szigetelőt teszünk a fegyverzetek közé). Ezen anyagok tulajdonságát jellemzi - relatív dielektromos állandó (permittivitás). A vákuumnak egységnyi ez az értéke.
Dielektrikumok kondenzátorban:
A kondenzátor kapacitása: 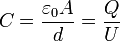 (ahol A a lemezek területe, d azok távolsága)
(ahol A a lemezek területe, d azok távolsága)
Kísérleti tapasztalat alapján, ha dielektrikumot teszünk a kondenzátorba, akkor megnő a kapacitás.
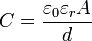 , ahol
, ahol 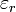 a dielektrikum relatív permittivitása.
a dielektrikum relatív permittivitása.
Mivel a töltések nem változnak, ezért a feszültségnek kell csökkennie. Viszont ez a potenciálkülönbség nem más, mint a fegyverzetek közötti térerősség vonalintegrálja. Ebből az következik, hogy a kondenzátoron belül csökkennie kellett a térerősségnek.
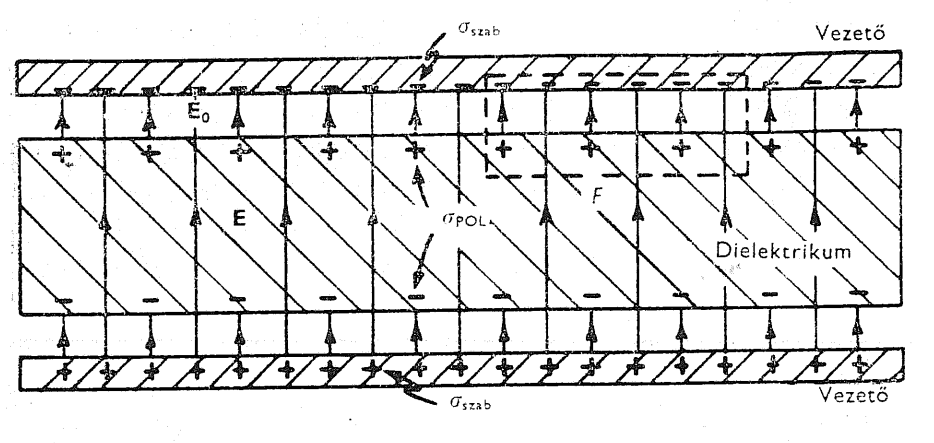
Ha alkalmazzuk a Gauss-tételt, és az ábrán látható (bekeretezett “dielektrikum”) felületre integrálunk, akkor a leutóbbi következtetésünk alapján arra jutunk, hogy kisebb lesz a töltéssűrűség. (Olyan, mintha két kis kondenzátort kötnénk sorba.) Ez csak akkor lehet, ha a szigetelő egyik felén pozitív, másik felén negatív töltés indukálódik. (Vezető esetén tényleg ezt is várnánk...)
A szigetelő semleges részecskékből áll, melyek külső tér hatására indukált dipólmomentumok lesznek. (Egy elég jól használható magyarázat: az elektronokra és a protonokra más irányú erők hatnak, így tozul a részecske, és az elektronok súlypotja nem esik egybe a protonéval egy részecskkén belül. Így kialakul egy dipólus.) Ha egy dipólban a két töltés távolsága 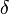 (ami a polarizációs vektor), akkor egy atom dipólusnyomatéka:
(ami a polarizációs vektor), akkor egy atom dipólusnyomatéka: 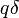 . Így bevezethető az egységnyi térfogatra eső dipólmomentum sűrűség:
. Így bevezethető az egységnyi térfogatra eső dipólmomentum sűrűség: 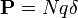 (ha a térrészban N részecske van)
(ha a térrészban N részecske van)
Ez az érték egyenesen arányos a térerősséggel: 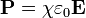 ahol
ahol 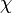 az anyagra jellemző elektromos szuszceptibilitás.
az anyagra jellemző elektromos szuszceptibilitás.
Az elektromos indukció felírása:
Fontos tudni, hogy a polarizáció NEM azonos a megosztás jelenvégével. Ez utóbbiban valódi töltések keletkeznek, és vándorolnak el a vezetőben, ezzel szemben a polarizációban csak atomi méretű töltésszétválás történik!
Számos anyag van amelyre a fenti lineáris összefügés nem igaz, a legérdekesebbek talán az elektrétek, amelyek állandó elektromos teret tartanak fennt, hasonlóan az állandó mágnesek mágneses teréhez.
Magnetosztatika [2]
A Magnetosztatikát leíró Maxwell-egyenletek:
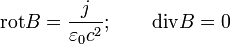
B a mágneses indukció vektora. Ezt a térerősséggel (H) a permeabilitás 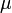 kapcsolja össze:
kapcsolja össze:
Az utolsó lépésben definiáltuk a mágneses szuszceptibilitást (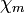 ) is, ez az adott anyag hatására megjelenő térnövekedést jellemzi. Bevezetjük továbbá M-et, ez a mágnesezettség, a térfogategység mágneses momentuma. Összefüggése H-val:
) is, ez az adott anyag hatására megjelenő térnövekedést jellemzi. Bevezetjük továbbá M-et, ez a mágnesezettség, a térfogategység mágneses momentuma. Összefüggése H-val:
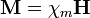
További összefüggések:
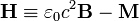
Jól látható az analógia 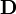 és
és 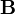 között.
között.
- Mágneses térben mozgó töltésre erő hat: Lorentz-erő - 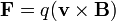
- Nyugalmi indukció (Fluxus-szabály) [3]:
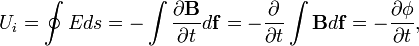 ahol
ahol 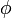 a mágneses tér fluxusa.
a mágneses tér fluxusa.
Mozgási indukciónál a Lorentz-erő alapján kell integrálnunk, de szintén visszakapjuk a Fluxus-szabályt.
Stacionárius áram, áramköri törvények: Kirchhoff-törvények, Ohm-törvény
A stacionárius áram kifejezés arra utal, hogy nincsen időbeli változása az áramnak. Ez állandó mágneses teret hoz létre maga körül. Gyakran használjuk a lineáris vezető kifejezést. Ez hasonló absztrakció, mint a ponttöltés bevezetése sztatikában. Itt arra kell gondolni, hogy adott egy görbe a térben, és ennek a görbének minden pontjában egy j áramsűrűség van, amely párhuzamos a görbe irányvektorával. Az áramot valamilyen potenciálkülönbség hajtja körben az áramkörben. Ezt valamilyen hatással (kémiai, mechanikai, stb.) létre kell hozni, és fenn kell tartani. Erre bevezetjük az elektromotoros erőt: ez azzal a térerősséggel egyenlő, amely a töltésszétválasztás során létrejött teret kompenzálja, ha nem folyik áram.
Kirchhoff törvények
Kirchhoff I.-II. törvénye eldinből:itt
- Huroktörvény: Egy zárt áramköri hurokban a feszültségek előjeles összege zérus (feltéve, hogy nincs külső mágneses tér).
- Csomópont-törvény: Az egy áramköri csomópontban összefutó áramok előjeles összege zérus.
Ohm-törvény
Általában: 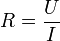
A lokális Ohm-törvény:
ahol 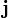 az áramsűrűség,
az áramsűrűség, 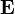 az elektromos térerősség,
az elektromos térerősség, 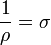 a fajlagos vezetőképesség és
a fajlagos vezetőképesség és 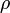 a fajlagos ellenállás. Fontos megjegyezni, hogy ezt sem tartalmazzák a Maxwell-egyenletek, tulajdonképpen ez is anyagi egyenlet. Lásd a kereszteffektusoknál található levezetést.
a fajlagos ellenállás. Fontos megjegyezni, hogy ezt sem tartalmazzák a Maxwell-egyenletek, tulajdonképpen ez is anyagi egyenlet. Lásd a kereszteffektusoknál található levezetést.
Érdemes megyjegyezni, hogy a kontinuitási egyenlet miatt az áramsűrűség normális komponense a határfelületeken egyenlő, azonban ha két olyan anyag van a két oldalon, amelyek vezetőképessége (ellenállása) más, akkor a térerősség is különböző kell, hogy legyen, és az eredmény az, hogy a felületen töltésfelhalmozódás alakul ki.
Mágneses hatások
Az egyenárammal átjárt lineáris vezető egy infinitezinális darabja által létrehozott mágneses teret a Biot-Savart-törvény adja meg. Ez egyszerűen levezethető a stacionáruis állapotot leíró Maxwell-egyenletekből. Az eredmény:
Ennek egy speciális alkalmazása, amit igen sokszor használ a fizika, az egyetlen kis áramhurok által látrehozott mágneses tér. Ha a hurokban I áram folyik, akkor bevezetjük a mágneses momentumot (hasonló az elektromos dipólhoz):
ahol az áramot a hurok által behatárolt felület nagyságával szoroztuk meg, az irányt a jobbkéz szabály adja. Ennek sehítségével a kis hurok mágneses tere:
Az így létrehozott térben a töltésekre természetesen hat a Lorentz-erő. Ennek következménye az is, hogy két párhuzamos lineáris vezető között erőhatás ébred, ha bennük áram folyik. Ennek mértéke:
Ha egy irányba folyik az áram a két vezetőben, akkor vonzzák egymást, ha ellentétesen, akkor taszítják egymást.
Tekercsek
Ha feltekerünk spirálba egy vezetőt, és áramot folyatunk át rajta, akkor az egyes hurkok mágneses tere összeadódik, továbbá jó közelítéssel a tekercsen belül homogén terünk lesz, ami a szélek felé egyre jobban leromlik. A létrehozott B tér egyenesen arányos az áramerősséggel, és a menetszámmal (n).
Hivatkozások: