Relativitáselmélet
Tartalomjegyzék
Kísérleti előzmények
Matematikai alapok és fogalmak
A relativitáselmélet matematikai alapjai
Relativisztikus kinematika és dinamika
Relativisztikus kinematika és dinamika
Relativisztikus elektrodinamika
Relativisztikus kvantummechanika
(ez egy külön oldal lenne, de nem sikerült egyből rájönnöm, hogy hogy kell új oldalt csinálni)
Ebben a részben 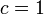
A Klein-Gordon egyenlet
Legyen 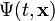 egy részecske hullámfüggvénye, mint egy inerciarendszerbeli tér- és időkoordináták skalárfüggvénye. Erre szeretnénk felírni egy kovariáns egyenletet, ami összhangban van a relativitáselmélettel. Ehhez induljunk ki a
egy részecske hullámfüggvénye, mint egy inerciarendszerbeli tér- és időkoordináták skalárfüggvénye. Erre szeretnénk felírni egy kovariáns egyenletet, ami összhangban van a relativitáselmélettel. Ehhez induljunk ki a 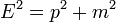 egyenletből, és helyettesítsük a fizikai mennyiségeket a klasszikus kvantummechanikából ismert operátoraikkal. Az impulzus operátora:
egyenletből, és helyettesítsük a fizikai mennyiségeket a klasszikus kvantummechanikából ismert operátoraikkal. Az impulzus operátora: 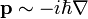 , az energiát az időderiváltnak feleltethetjük meg:
, az energiát az időderiváltnak feleltethetjük meg: 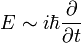 , a tömeg pedig itt is egy állandó. Így a fenti egyenletnek megfelelő operátorokat a hullámfüggvényre hattatva a következő egyenletet kapjuk:
, a tömeg pedig itt is egy állandó. Így a fenti egyenletnek megfelelő operátorokat a hullámfüggvényre hattatva a következő egyenletet kapjuk:
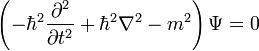
Ez a Klein-Gordon egyenlet. Ezt felírhatjuk négyesvektoros alakban is. Az energia és impulzus közötti összefüggés (diszperziós reláció) négyesvektorosan: 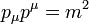 . Az előző megfeleltetés operátoroknak ekkor:
. Az előző megfeleltetés operátoroknak ekkor: 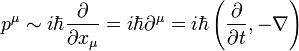 . A Klein-Gordon egyenlet ilyen alakban:
. A Klein-Gordon egyenlet ilyen alakban:
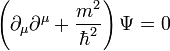
A Klein-Gordon egyenlet síkhullám megoldásait egyszerűen felírhatjuk:
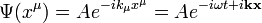
Ezt az egyenletbe behelyettesítve láthatjuk, hogy kielégíti azt, ha teljesül a 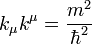 feltétel. Ez azt jelenti, hogy a
feltétel. Ez azt jelenti, hogy a 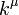 négyesvektor komponenseiből csak 3 független. Legyyenek a komponensek:
négyesvektor komponenseiből csak 3 független. Legyyenek a komponensek: 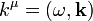 , így ezekre a
, így ezekre a 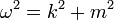 diszperziós reláció adódik. A kvantummechanikában szokásos értelmezés szerint az energia (ez az időderiválás operátor sajátértéke is)
diszperziós reláció adódik. A kvantummechanikában szokásos értelmezés szerint az energia (ez az időderiválás operátor sajátértéke is) 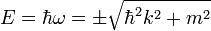 . Formálisan a pozitív energiás megoldás mellett van egy negatív energiájú is (ez jelenti majd az antirészecskéket).
. Formálisan a pozitív energiás megoldás mellett van egy negatív energiájú is (ez jelenti majd az antirészecskéket).
Eddig még nem beszéltünk arról, hogy milyen részecskék leírására alkalmas a Klein-Gordon egyenlet, felmerül a kérdés, hogy ez az egyenlet alkalmas-e a Schrödinger egyenlet relativisztikus általánosításaként. Elvileg ezzel az egyenlettel 0 spinű részecskéket lehetne leírni, a valóságban azonban nincs olyan elemi részecske, amit csak a Klein-Gordon egyenlet írna le (a fotonokra felírható hullámegyenletek hasonlóak, de ott nem egy skalármező, hanem a potenciálokból álló négyesvektor komponensei szerepelnek). Ennek ellenére érdemes megvizsgálni, hogyha lennének ilyen részecskék, akkor milyen tulajdonságokkal rendelkeznének. A Schrödinger-egyenletnél a hullámfüggvény abszolútértékének négyzete megtalálási valószínűségsűrűségként volt értelmezhető. Kérdéses, hogy itt lehet-e ehhez hasonló megállapításokat tenni. Ehhez írjuk fel a Klein-Gordon egyenletet és a komplex konjugáltját:
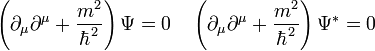
Szorozzuk meg az eredeti egyenletet (balról) 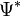 -al, a komplex konjugált egyenletet
-al, a komplex konjugált egyenletet 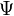 -vel, és vonjuk ki a kettőt egymásból. Az eredmény:
-vel, és vonjuk ki a kettőt egymásból. Az eredmény:
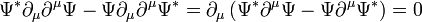
Azt kaptuk, hogy egy négyesvektor divergenciája 0. Ez lehetőséget ad egy négyesáram bevezetésére, amire egy megmaradási tétel (kontinuitási egyenlet) írható fel. Legyen:
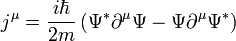
Ekkor fennáll, hogy 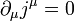 . A komponenseket
. A komponenseket 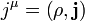 formában írva ez egy kontinuitási egyenlet jelent:
formában írva ez egy kontinuitási egyenlet jelent:
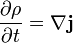
Az egész térre integrálva azt kapjuk, hogy a 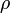 sűrűség integrálja állandó:
sűrűség integrálja állandó:
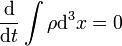
Ez alapján azt lehetne mondani, hogy 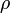 a Schrödinger egyenletnél bevezethető valószínűségsűrűséghez hasonlóan viselkedik, ennek ellenére nem lehet valószínűségsűrűségként értelmezni, mert a Schrödinger-egyenletnél használt abszolútértéknégyzettel szemben
a Schrödinger egyenletnél bevezethető valószínűségsűrűséghez hasonlóan viselkedik, ennek ellenére nem lehet valószínűségsűrűségként értelmezni, mert a Schrödinger-egyenletnél használt abszolútértéknégyzettel szemben 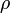 értéke nem csak pozitív lehet, hanem negatív is. Ez abból következik, hogy a Klein-Gordon egyenlet időben másodrendű, így kezdőfeltételként
értéke nem csak pozitív lehet, hanem negatív is. Ez abból következik, hogy a Klein-Gordon egyenlet időben másodrendű, így kezdőfeltételként 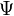 -t és az idő szerinti deriváltját tetszőlegesen lehet megválasztani, úgy is, hogy
-t és az idő szerinti deriváltját tetszőlegesen lehet megválasztani, úgy is, hogy 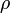 egyes helyeken negatív legyen.
egyes helyeken negatív legyen.
Így a Klein-Gordon megoldásainak nem lehet a Schrödinger-egyenletnél megszokott valószínűségi értelmezést adni. Abban az esetben viszont, ha töltött részecskékről van szó, egy töltés áramsűrűséget lehet bevezetni. Legyen ekkor:
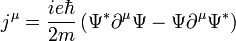
Az előző definícióhoz képest az egyetlen eltérés a részecskék töltésegységét jelentő  szorzó, így
szorzó, így 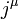 négyes áramsűrűségként értelmezhető (a kontinuitási egyenlet ugyanúgy teljesül rá). A nulladik komponenes a töltéssűrűség:
négyes áramsűrűségként értelmezhető (a kontinuitási egyenlet ugyanúgy teljesül rá). A nulladik komponenes a töltéssűrűség:
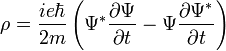
A térszerű komponensek a hármas áramsűrűséget adják:
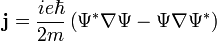
Az össztöltés megmarad:
Értelmezés sikertelen (Hiányzó <code>texvc</code> végrehajtható fájl; a beállítást lásd a math/README fájlban.): Q \eqiuv \int \rho \operatorname{d}^3 x \quad \rightarrow \quad \frac{\operatorname{d} Q}{\operatorname{d} t} = 0
Ezzel szemben 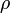 értéke egy adott pontban tetszőlegesen változhat, lehet pozitív és negatív is. Ez azt jelenti, hogy a Klein-Gordon egyenlettel nem lehet egy rögzített (pozitív vagy negatív) töltésű részecskét leírni, az időfejlődés során megjelenhetnek ellentétes töltésű tartományok, ennek magyarázata az, hogy minden részecskének létezik ellentétes töltésű antirészecskéje, és a részecskék és antirészecskék száma nem marad meg, csak az össztöltés, keletkezhetnek és annihilálódhatnak részecske-antirészecske párok. Ennek a teljes leírására azonban a Klein-Gordon egyenlet jelenlegi formája nem alkalmas, el kell végezni a
értéke egy adott pontban tetszőlegesen változhat, lehet pozitív és negatív is. Ez azt jelenti, hogy a Klein-Gordon egyenlettel nem lehet egy rögzített (pozitív vagy negatív) töltésű részecskét leírni, az időfejlődés során megjelenhetnek ellentétes töltésű tartományok, ennek magyarázata az, hogy minden részecskének létezik ellentétes töltésű antirészecskéje, és a részecskék és antirészecskék száma nem marad meg, csak az össztöltés, keletkezhetnek és annihilálódhatnak részecske-antirészecske párok. Ennek a teljes leírására azonban a Klein-Gordon egyenlet jelenlegi formája nem alkalmas, el kell végezni a 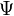 tér második kvantálását. Ezt itt nem tesszük meg, az antirészecskék jelenlétét viszont a síkhullám megoldásokon is tudjuk egyszerűen szemléltetni. Ehhez írjuk fel az előbbi síkhullám megoldást (a szokásos
tér második kvantálását. Ezt itt nem tesszük meg, az antirészecskék jelenlétét viszont a síkhullám megoldásokon is tudjuk egyszerűen szemléltetni. Ehhez írjuk fel az előbbi síkhullám megoldást (a szokásos 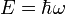 és
és 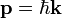 jelöléseket használva):
jelöléseket használva):
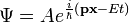
Itt 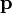 tetszőleges (hármas) vektor, és érvényes az
tetszőleges (hármas) vektor, és érvényes az 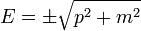 diszperziós reláció. Legyen a pozitív megoldás
diszperziós reláció. Legyen a pozitív megoldás 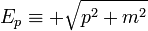 , így
, így 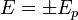 , a különböző előjelhez tartozó megoldások külön felírva:
, a különböző előjelhez tartozó megoldások külön felírva:

Az ezekből számolt töltéssűrűségek (a deriválást elvégezve):

Az egyik esetben a töltéssűrűség pozitív, a másikban negatív. Ezt úgy lehet értelmezni, hogy a 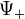 megoldás
megoldás 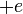 töltésű, a
töltésű, a 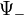 megoldás
megoldás 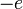 töltésű részecskéket ír le.
töltésű részecskéket ír le.