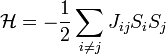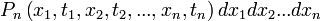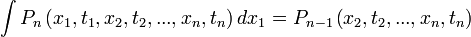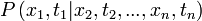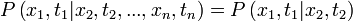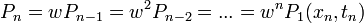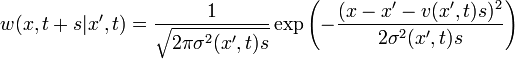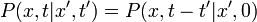„Sztochasztikus folyamatok” változatai közötti eltérés
(→Spinüvegek) |
|||
| 3. sor: | 3. sor: | ||
== Kauffman-hálózat == | == Kauffman-hálózat == | ||
== Spinüvegek == | == Spinüvegek == | ||
| − | + | Közismert, hogyha mágneses momentumokat (spineket) akarunk elhelyezni egy háromszögrácson, antiferromágneses csatolás mellett, akkor az frusztrált lesz: például egy háromszög két csúcsára leteszünk ellenkező beállással 1-1 spint, akkor a harmadiknak nincs optimális beállása. | |
| + | |||
| + | A spinüvegekben hasonló frusztrációk vannak, rendezetlen rácson. Úgy lehet elképzelni, hogy a spinek véletlenszerű helyeken, véletlenszerű (ferro- vagy antiferromágneses) kölcsönhatásokkal vannak összekötve. Ennek eredményeképpen a külső térre adott válaszuk igen bonyolult, számos különböző időskálán zajlik. A leírásuk is igen nehézkes. | ||
| + | |||
| + | Egy konkrét gyakran használt modellben, a Sherrington-Kirkpatrick modellben a spinek között a szokásos Hamilton írja le a kölcsönhatást: | ||
| + | |||
| + | :<math>\mathcal{H} = -\frac{1}{2}\sum_{i\ne j} J_{ij}S_i S_j</math> | ||
| + | |||
| + | de <math>J</math> egy véletlen valószínűségi változó Gauss-eloszlással. Ebben az esetben az átlagos szabadenergia kiszámolható a rendszerre zárt alakban, két fizikailag értelems paraméterrel kifejezve: az egyik paraméter eredő mágnesezettség jellegű, a másik a mágnesezettség szórását jellemzi. A spinüveg helyzetnek az felel meg, amikor az eredő mágnesezettség eltűnik, de a szórás véges, szemben például a ferromágneses renddel, ahol az eredő mágnesezettség nem zérus. | ||
| + | |||
| + | A fázisteret két paraméterrel lehet felmérni: a csatolás relatív szórásával (a fenti Gauss átlaga osztva a szórásával) valamint a csatolás szórásának és a hőmérsékleti energiának (kT) az arányával. Ezen a diagrammon a spinüveg fázis akkor jön létre, amikor a csatolás erősebb a hőmérsékleti fluktuációknál, de a relatív szórása igen nagy. | ||
| + | |||
== Markov-lánc, Markov-folyamatok == | == Markov-lánc, Markov-folyamatok == | ||
Egy sztochasztikus folyamatot jellemezhetünk azzal, hogy diszkrét időpillanatokban a tekintett valószínűségi változó milyen értékeket vett fel. Egy rendszert akkor tekintünk leírtnak, ha meg tudjuk mondani minden időpillanatra, minden értékre a megfelelő valószínűségeket: | Egy sztochasztikus folyamatot jellemezhetünk azzal, hogy diszkrét időpillanatokban a tekintett valószínűségi változó milyen értékeket vett fel. Egy rendszert akkor tekintünk leírtnak, ha meg tudjuk mondani minden időpillanatra, minden értékre a megfelelő valószínűségeket: | ||
A lap 2011. június 12., 12:32-kori változata
Az alábbiakban néhány véletlenszerű folyamatot és ezek leírási módszereit tárgyaljuk.
Kauffman-hálózat
Spinüvegek
Közismert, hogyha mágneses momentumokat (spineket) akarunk elhelyezni egy háromszögrácson, antiferromágneses csatolás mellett, akkor az frusztrált lesz: például egy háromszög két csúcsára leteszünk ellenkező beállással 1-1 spint, akkor a harmadiknak nincs optimális beállása.
A spinüvegekben hasonló frusztrációk vannak, rendezetlen rácson. Úgy lehet elképzelni, hogy a spinek véletlenszerű helyeken, véletlenszerű (ferro- vagy antiferromágneses) kölcsönhatásokkal vannak összekötve. Ennek eredményeképpen a külső térre adott válaszuk igen bonyolult, számos különböző időskálán zajlik. A leírásuk is igen nehézkes.
Egy konkrét gyakran használt modellben, a Sherrington-Kirkpatrick modellben a spinek között a szokásos Hamilton írja le a kölcsönhatást:
de 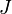 egy véletlen valószínűségi változó Gauss-eloszlással. Ebben az esetben az átlagos szabadenergia kiszámolható a rendszerre zárt alakban, két fizikailag értelems paraméterrel kifejezve: az egyik paraméter eredő mágnesezettség jellegű, a másik a mágnesezettség szórását jellemzi. A spinüveg helyzetnek az felel meg, amikor az eredő mágnesezettség eltűnik, de a szórás véges, szemben például a ferromágneses renddel, ahol az eredő mágnesezettség nem zérus.
egy véletlen valószínűségi változó Gauss-eloszlással. Ebben az esetben az átlagos szabadenergia kiszámolható a rendszerre zárt alakban, két fizikailag értelems paraméterrel kifejezve: az egyik paraméter eredő mágnesezettség jellegű, a másik a mágnesezettség szórását jellemzi. A spinüveg helyzetnek az felel meg, amikor az eredő mágnesezettség eltűnik, de a szórás véges, szemben például a ferromágneses renddel, ahol az eredő mágnesezettség nem zérus.
A fázisteret két paraméterrel lehet felmérni: a csatolás relatív szórásával (a fenti Gauss átlaga osztva a szórásával) valamint a csatolás szórásának és a hőmérsékleti energiának (kT) az arányával. Ezen a diagrammon a spinüveg fázis akkor jön létre, amikor a csatolás erősebb a hőmérsékleti fluktuációknál, de a relatív szórása igen nagy.
Markov-lánc, Markov-folyamatok
Egy sztochasztikus folyamatot jellemezhetünk azzal, hogy diszkrét időpillanatokban a tekintett valószínűségi változó milyen értékeket vett fel. Egy rendszert akkor tekintünk leírtnak, ha meg tudjuk mondani minden időpillanatra, minden értékre a megfelelő valószínűségeket:
ahol 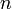 a leírni kívánt lépések száma. Mivel ez egy valószínűség, ezért minden
a leírni kívánt lépések száma. Mivel ez egy valószínűség, ezért minden 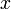 változójára kiintegrálva 1-et kell kapnunk, ez a norma-feltétel. Ezen felül, ha csak egy x változóra integrálunk, akkor az eggyel kisebb "rendű" valószínűségi kifejezést kell kapnunk:
változójára kiintegrálva 1-et kell kapnunk, ez a norma-feltétel. Ezen felül, ha csak egy x változóra integrálunk, akkor az eggyel kisebb "rendű" valószínűségi kifejezést kell kapnunk:
Tehát ha az egyik mintavételi időpontban minden lehetséges kimenetelre integrálunk, akkor olyan, mintha azt a pontot nem vennénk figyelembe. Ez a kompatibilitási feltétel.
Markov-folyamatoknál a rendszer jövőbeli állapotainak valószínűségét a korábbi, ismert állapotokból szeretnénk meghatározni. Ennek megfelelően ezt egy feltételes valószínűséggel fogalmazhatjuk meg:
azaz, ha ismert a rendszer vislkedése 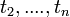 pillanatokban, akkor emellett a feltétel mellett milyen valószínűséggel lesz
pillanatokban, akkor emellett a feltétel mellett milyen valószínűséggel lesz 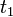 -ben
-ben 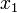 állapotban. Egy folyamat akkor Markov-folyamat, ha rendelkezik a Markov-tulajdonsággal, ami azt mondja, hogy a rendszer csak a legutóbbi állpotától függ:
állapotban. Egy folyamat akkor Markov-folyamat, ha rendelkezik a Markov-tulajdonsággal, ami azt mondja, hogy a rendszer csak a legutóbbi állpotától függ:
Ebből következik, hogyha 1 pontban ismert a Markov-folyamat, valamint az átmeneti valószínűségek, akkor teljes rendszer ismert, mert rekurzívan minden következő (vagy megelőző) állapot felírható az átmeneti valószínűségekkel:
Például ha egy diffúziós-folyamatot szeretnénk leírni, akkor az átmeneti valószínűség Gauss:
Homogénnek nevezzük a Markov-folyamatot, ha az átmeneti valószínűég időeltolás-invariáns:
Homogén diffúziós folyamatokra eben a kontextusban is levezethető a Fokker-Planck-egyenlet, ami lényegében a valószínűség-áramsűrűség megmaradását fejezi ki: