Master-egyenletek
Inkább Langevin gondolatvilágából következik (formalizmusában viszont inkább Einsteint követi).
Tartalomjegyzék
Alapvetése
- Megfigyelek valamit, amit valamilyen háttér befolyásol.
- A háttér annyira nem fontos, csak a hatása a megfigyelt részecskére (van néhány kiválasztott szabadsági fokom).
- Mivel a háttérről nem sokat tudok, valószínűségi egyenletekkel dolgozom.
Példa
Van egy rendszerem, amiből engem csak a mágneses viselkedés érdekel, csak a spineket figyelem.
Nagy rendszer: sok spin 
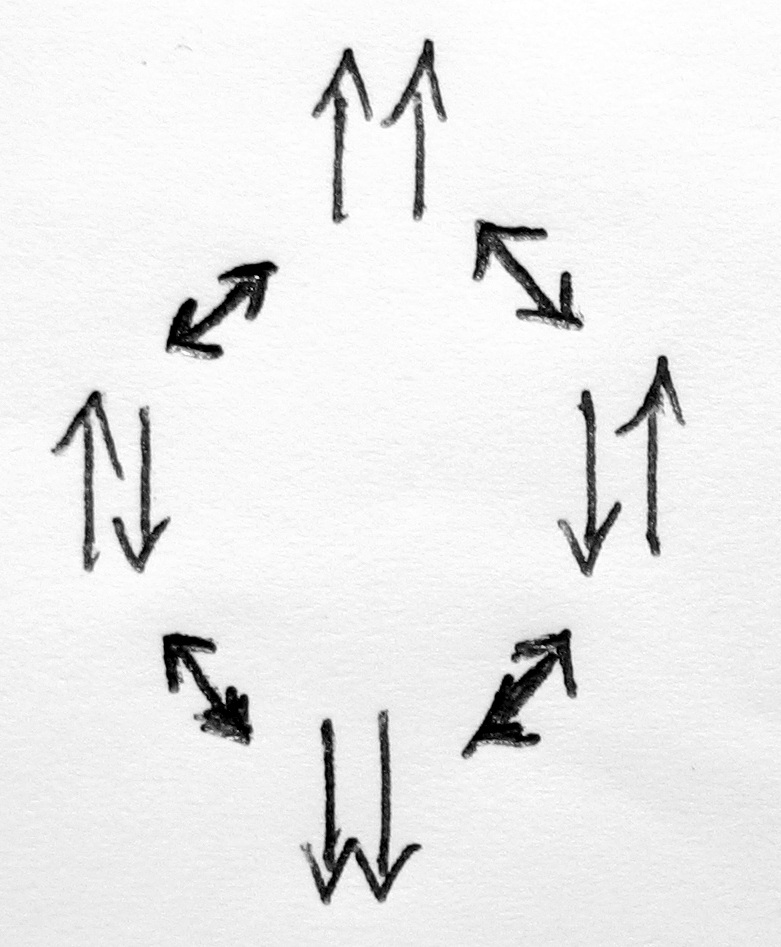
Két részecskéből álló rendszer esetén a teljes állapottér négy diszkrét állapotból áll:
A Master-egyenlet felírása
Most legyen n diszkrét állappot.
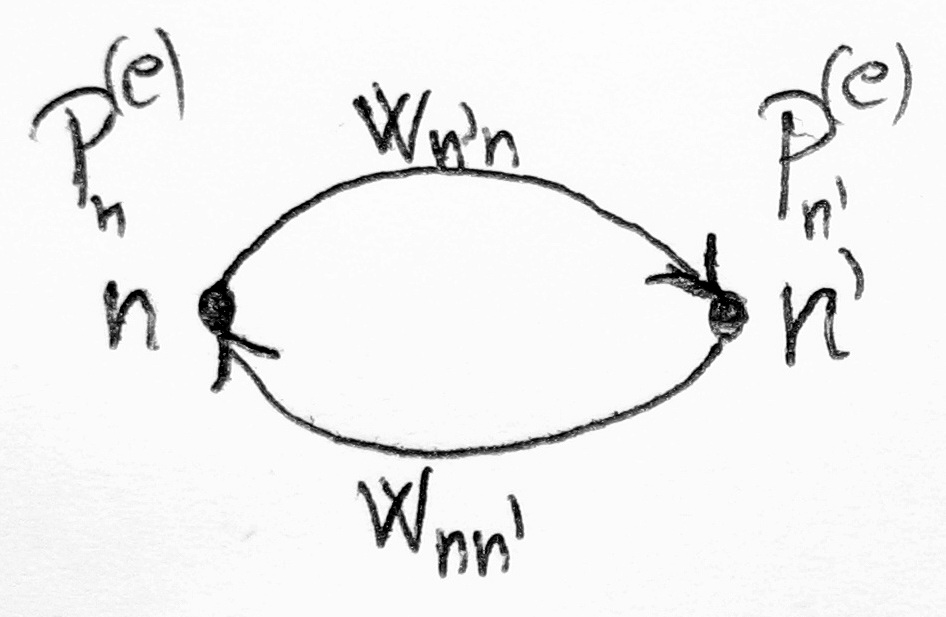
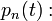 mi annak a valószínűsége, hogy a rendszer az n-edik állapotban van?
mi annak a valószínűsége, hogy a rendszer az n-edik állapotban van?
- Tegyük fel, hogy tudom, hogy egységnyi idő alatt mi annak a valószínűsége, hogy a rendszer n-ből n' állapotba megy át.
Ennek jelölése: 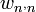 --> nem tudunk róla semmit, de tegyük fel, hogy ismerjük az értékét.
--> nem tudunk róla semmit, de tegyük fel, hogy ismerjük az értékét.
- Fermi aranyszabály:
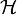 ismert,
ismert, 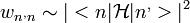 QM-ben.
QM-ben.
Ising [1] spin-rendszer esetén: 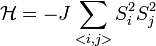 , ahol
, ahol 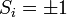 [1][2]
[1][2]
- Tegyük fel, hogy a folyamat Markov-folyamat, tehát létezik olyan
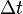 , hogy már csak a t mondja meg, hogy mi történik
, hogy már csak a t mondja meg, hogy mi történik 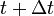 -ben. (És tegyük fel, hogy az átmenetek megvalósulnak.)
-ben. (És tegyük fel, hogy az átmenetek megvalósulnak.)
Ekkor:
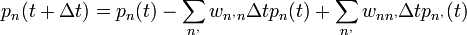
A 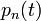 -t ismerem, a
-t ismerem, a 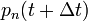 -t keresem, a
-t keresem, a 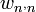 és
és 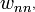 egységnyi időre vonatkozik.
egységnyi időre vonatkozik.
Sorbafejtek 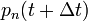 körül,
körül, 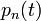 kiesik, így:
kiesik, így:
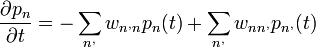
A Master-egyenlet diszkrét állapottérben
Ennek kell, hogy legyen stacionárius megoldása, amihez relaxál:
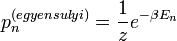 , ahol
, ahol 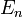 az n-edik állapot energiája.
az n-edik állapot energiája.
Ha ezt helyettesítem be, akkor a bal oldal 0 lesz-->ez 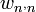 és
és 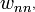 -re megkötés!
-re megkötés!
Van időtükrözési invariancia is! Ennek következménye a részletes egyensúly (bővebben később).
- Tegyük fel, hogy meg tudom úgy adni az átmeneti valószínűségeket, hogy a rendszer beugorjon az egyensúlyi állapotba.
- Hogyan kell megválasztani az átmeneti valószínűségeket?
Példa
Szilárd testekben lévő spinrendszereknél a többi kölcsönhatás hőtartályként adódik a rendszerhez. (Pl. szupravezetésnél feltételezték, hogy az elektronok Coulomb-kölcsönhatása le van árnyékolva, a fononok pedig a háttér hőtartályt adják. Később kiderült, hogy alacsony hőmérsékleten éppen a fononok miatt kezdik el vonzani egymást az elektronok.)
Az átmeneti valószínűségek megválasztása
- Egyensúlyban időtükrözési szimmetria van.
Számolom, hogy (irány szerint megkülönböztetve) hányszor megy egyikből a másik állapotba a rendszer.
- Stacionárius állapotban
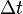 idő alatt az átmenetek száma:
idő alatt az átmenetek száma:
- n-ből n'-be menve:
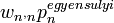
- n'-ből n-be menve:
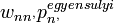
- n-ből n'-be menve:
- A részletes egyensúly elve azt mondja ki, hogy a két számnak meg kell egyeznie, azaz:
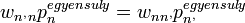
Megkötés az átmeneti valószínűségek hányadosára
Ha az állapotok száma véges és a rendszer minden pontjából minden másik pontjába el tudok jutni, akkor egyetlen stacionárius állapot lesz, az egyensúlyi.
Csak az átmeneti valószínűségek hányadosára van megkötés, azaz:
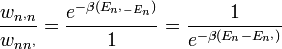
Ha 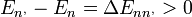 (azaz az energia nő), az e-ados tag 1-nél kisebb lesz, tehát vehetem azt az átmeneti valószínűségnek. Ha csökken az energia, akkor az energiacsökkenés felé vivő lépést egy valószínűséggel lépem meg.
(azaz az energia nő), az e-ados tag 1-nél kisebb lesz, tehát vehetem azt az átmeneti valószínűségnek. Ha csökken az energia, akkor az energiacsökkenés felé vivő lépést egy valószínűséggel lépem meg.
Bizonyítás: 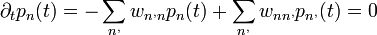 (egyensúly esetén). Tehát:
(egyensúly esetén). Tehát:
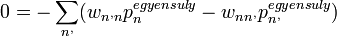 Páronként kioltják egymást. Ezért hívják részletes egyensúlynak, mivel nem csak az egész összeg nulla, hanem az állapotok között páronként van egyensúly.
Páronként kioltják egymást. Ezért hívják részletes egyensúlynak, mivel nem csak az egész összeg nulla, hanem az állapotok között páronként van egyensúly.
A dinamikai mátrix felírása
Egy N-állapotú rendszer adott állapotainak valószínűségeit - időtől függően - felírhatjuk vektoros alakban, a következőképpen:
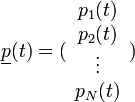
Ekkor 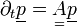 [3] és:
[3] és:
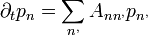
, ahol 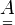 a rendszer dinamikai mátrixa, kiszámítása pedig a következőképpen történik:
a rendszer dinamikai mátrixa, kiszámítása pedig a következőképpen történik:
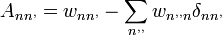
A rendszer dinamikai mátrixának kiszámítási módja
A mátrix elemeit összeadva a következőket kapjuk:
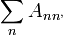 [4]
[4] 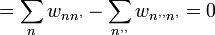 [5]
[5]
Perron-Frobenius teoréma [2]
A fenti mátrix 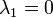 sajátértéke a legnagyobb, nem degenerált sajátállapothoz tartozik. Ez tulajdonképpen azt jelenti, hogy létezik egy (és csak egy) olyan megoldás, amire a sajátérték nulla. A legkisebb sajátérték sem degenerált.
sajátértéke a legnagyobb, nem degenerált sajátállapothoz tartozik. Ez tulajdonképpen azt jelenti, hogy létezik egy (és csak egy) olyan megoldás, amire a sajátérték nulla. A legkisebb sajátérték sem degenerált.
Ha az egyensúlyi állapotban 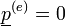 (ekkor
(ekkor 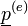 minden komponense pozitív [6]), akkor
minden komponense pozitív [6]), akkor 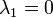 . Ekkor:
. Ekkor:
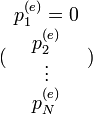 .
Azaz egyensúlyban az egyes állapot kiürül. Részletes egyensúlyban emiatt minden állapot ki fog ürülni.
.
Azaz egyensúlyban az egyes állapot kiürül. Részletes egyensúlyban emiatt minden állapot ki fog ürülni.
Ha a többi 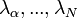 sajátértékhez nézzük az időfejlődést, pl.:
sajátértékhez nézzük az időfejlődést, pl.: 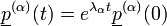 . Látható, hogy ebben az esetben a rendszer divergál. Azonban ha a sajátértékek mindegyike
. Látható, hogy ebben az esetben a rendszer divergál. Azonban ha a sajátértékek mindegyike 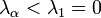 , akkor a rendszer az egyensúlyi állapothoz fog konvergálni az időfejlődése során.
, akkor a rendszer az egyensúlyi állapothoz fog konvergálni az időfejlődése során.
Tegyük fel, hogy mégis degenerált a 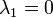 sajátérték, ekkor van másik egyensúlyi állapot:
sajátérték, ekkor van másik egyensúlyi állapot:
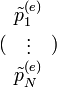
De ha van két ilyen állapot, akkor azok lineárkombinációja is egyensúlyi állapot (mivel a Master-egyenlet lineáris):
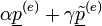 .
.
Ám ekkor meg tudom tenni - alfa és gamma értékek változtatásával -, hogy minden tagot pozitívnak választok, kivéve egyet, ami nulla. Vagyis a két vektor egyenlő kell, hogy legyen.[7]
A fentiek fényében tehát:
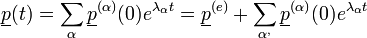
Ahol az egyenlet végén lévő szummás tagok kihalnak, mivel a 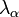 -k negatívak (egyébként a megoldás - ahogy fentebb láttuk - elszaladna a végtelenbe).
-k negatívak (egyébként a megoldás - ahogy fentebb láttuk - elszaladna a végtelenbe).
Megjegyzés: fázisátalakulásnál nagyok a fluktuációk, mivel az egész rendszer együtt változik, ellentétben a magas hőmérsékleten lévő kis fluktuűciókkal. Ez a 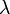 -k értékeiben azt jelenti, hogy (
-k értékeiben azt jelenti, hogy (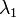 ugye mindig nulla,)
ugye mindig nulla,) 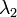 abszolútértékben nagyon kicsi, mert reciproka adja a relaxációs időt:
abszolútértékben nagyon kicsi, mert reciproka adja a relaxációs időt:
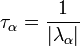
És most jöjjön egy levezetés.
Két spinből álló rendszer átmeneti valószínűségeinek meghatározása
Tehát rendszerünk két spinből áll, amit egy négy elemű gráfon ábrázolhatunk.
Egyszerre csak egy spin fordulhat!
Az állapotok közötti átmeneti valószínűségek meghatározásához először az egyennsúlyi valószínűségeket kell meghatároznunk.
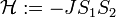 és
és 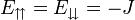 , valamint
, valamint 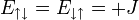
Tudjuk még továbbá, hogy:
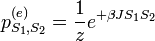 , ahol z az állapotösszeg, értéke pedig:
, ahol z az állapotösszeg, értéke pedig:
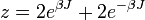 , ahol a
, ahol a 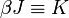 . Ezt az átnevezést elvégezve az egyensúlyi valószínűségek a következő képlettel írhatóak le:
. Ezt az átnevezést elvégezve az egyensúlyi valószínűségek a következő képlettel írhatóak le:
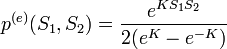
Jelölés: 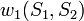 . Jelentése: bármelyik
. Jelentése: bármelyik  állapotban vagyunk, és az egyes(!) spint forgatjuk. Érdemes megjegyezni, hogy a
állapotban vagyunk, és az egyes(!) spint forgatjuk. Érdemes megjegyezni, hogy a 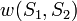 átmeneti valószínűségek 1/idő dimenziójúak.
átmeneti valószínűségek 1/idő dimenziójúak.
Ezen okból az átmeneti valószínűségek hányadosára a következő értékeket kaphajuk:
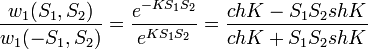
Az egyenlet bal oldalán lévő felső tört felső része annak valószínűsége, hogy 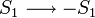 állapotátmenet történik meg, míg alsó része ennek pont az ellenkezője. Az e-ados alakokat azért lehet a fenti módon átalakítani, mert kihasználtuk, hogy a spinek csak
állapotátmenet történik meg, míg alsó része ennek pont az ellenkezője. Az e-ados alakokat azért lehet a fenti módon átalakítani, mert kihasználtuk, hogy a spinek csak 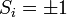 értékeket vehetnek fel.
értékeket vehetnek fel.
Végezzük el a 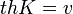 helyettesítést, ekkor a következőt kapjuk:
helyettesítést, ekkor a következőt kapjuk:
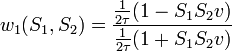 Ebből következpen:
Ebből következpen: 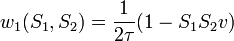 [8]
[8]
Ugyanezt 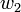 -re felírva:
-re felírva:
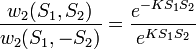
Lábjegyzetek
- ↑ A ferromágnes első modellje. A spinek egy irányba szeretnek beállni, de a hőmozgás szétválasztja őket. T->0: Curie-hőmérséklet alatt ferromágneses viselkedés.
- ↑ A Fermi aranyszabály és az Ising spin-rendszer csak a spineket vizsgálja, nálunk meg egy csomó más hatás is van, tehát nem pont azt írják le, ami nekünk kell.
- ↑ Miért is? Erre itt nem emlékszem, hogy miért...:(
- ↑ Az egységmátrixot hozzáadva sztochasztikus mátrixnak nevezzük.
- ↑ A két szummás tag egyenlő adott értéknél, csak az összegzési index más.
- ↑ Itt sem teljesen értem, hogy mire gondoltunk, de így van felírva. Elírtam?
- ↑ Szerintem itt a magyarázatom nem túl világos. Én sem teljesen emlékszem, hogy miért is volt ez így. Ha valaki világosabbat tud, írja be legyen szíves!
- ↑ Ha
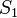 vagy
vagy 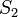 előjele változik, az egyenletben lévő előjel változik csak, azaz
előjele változik, az egyenletben lévő előjel változik csak, azaz 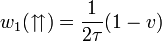 és
és 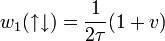 (v pedig mindig pozitív!)
(v pedig mindig pozitív!)