Maxwell-egyenletek
Az egyenletek összegzése
Maxwell négy egyenlete a következőket írja le,
- 1. Az elektromos tér forrásos, azaz elektromos töltés jelenlétében erővonalak indulnak a pozitív töltésekről, melyek a negatív töltéseken végződnek. (Gauss-törvény)
- 2. A mágneses indukció változása elektromos teret indukál, melynek iránya ellenkező mint az őt létrehozó változás. (A Lenz-törvény és Faraday indukciós törvényének egyesítése)
- 3. A mágneses tér forrásmentes, azaz a mágneses tér erővonalai önmagukba záródnak. (Gauss mágneses törvénye),
- 4. Az elektromos áram, illetve a folytonossági egyenlet kielégítéséből adódó eltolási áram mágneses teret hoz létre. (Ampère-törvény)
A makroszkopikus egyenletek SI mértékegységrendszerben:
| Megnevezés | Sorszám | Differenciális alak | Integrális alak |
|---|---|---|---|
| Gauss-törvény | I. | 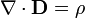
|
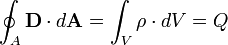
|
| Faraday-Lenz-törvény | II. | 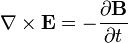
|
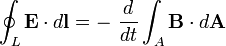
|
| Gauss mágneses törvénye |
III. | 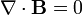
|
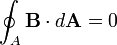
|
| Ampère-törvény |
IV. | 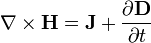
|
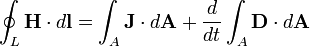
|
| Jelölés | Név | SI mértékegység |
|---|---|---|
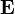
|
elektromos térerősség | volt per méter: 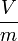
|
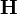
|
mágneses térerősség | amper per méter: 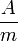
|
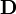
|
elektromos indukció | amperszekundum per négyzetméter: 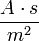
|
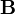
|
mágneses indukció | Voltszekundum per négyzetméter vagy tesla: 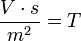
|
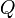
|
elektromos töltés | amperszekundum vagy coulomb: 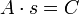
|
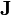
|
áramsűrűség | amper per négyzetméter: 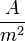
|
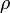
|
elektromos töltéssűrűség | coulomb per köbméter: 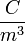
|