Relativisztikus kinematika és dinamika
Tartalomjegyzék
Pontrészecske pályájának a leírása
Egy pontrészecske mozgását egy inerciarendszerből nézve megadhatjuk annak a pályáját (azaz a 4-es helyvektort) valamilyen paraméter függvényében. Az egyik legegyszerűbb választásnak tűnik, hogyha a részecske koordinátáit az inerciarendszerbeli idő függvényében adjuk meg. Sok esetben hasznosabb viszont, ha a koordinátákat az eltelt sajátidő függvényében adjuk meg (azaz a 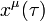 függvényt adjuk meg), ami a geometriában a görbék ívhossz szerinti paraméterezésének felel meg (az sajátidő az ívhosszal arányos).
függvényt adjuk meg), ami a geometriában a görbék ívhossz szerinti paraméterezésének felel meg (az sajátidő az ívhosszal arányos).
A részecske sebességénél egy adott rendszerből nézve megadhatjuk az abban a rendszerben mért sebességet (a koordináták idő szerinti deriváltját), ez az adott rendszerben jellemzi a mozgást. (Az idő egy négyesvektor komponense, így minden rendszerben más, így az idő szerinti deriválás eredménye nem lesz négyesvektor.)
Hasznos bevezetni a részecske 4-es sebességét, ami a helykoordinátáknak a sajátidő szerinti deriváltja:
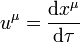
Mivel a hely négyesvektor és a sajátidő skalár, ezért a négyessebesség is 4-esvektor lesz, viszont a komponensei nem mérhetőek közvetlenül, a szokásos sebességméréssel a klasszikus mechanikában megszokott hármas sebességet tudjuk mérni. Kihasználva a sajátidőre vonatkozó 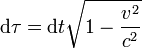 összefüggést, a négyessebesség komponensei kifejezhetőek a mérhető hármas sebességgel:
összefüggést, a négyessebesség komponensei kifejezhetőek a mérhető hármas sebességgel:
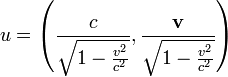
Itt 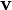 a hármas sebesség (a helykoordináták idő szerinti deriváltja a megfigyelő inerciarendszerében).
a hármas sebesség (a helykoordináták idő szerinti deriváltja a megfigyelő inerciarendszerében).
A négyessebesség abszolútértéke:
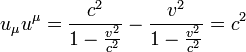
Érdemes még definiálni a négyes gyorsulást is, amit a négyessebesség további (sajátidő szerinti) deriválásával kapunk:
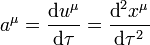
A négyessebesség abszolútértékére kapott egyenlőség deriválásával könnyen belátható a 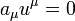 összefüggés is.
összefüggés is.
Egyenletesen gyorsuló mozgás
(ez egy jól követhető, szemléletes példa lenne az előző szakaszban bevezetett fogalmakra és gyakorlati alkalmazásukra)
Dinamika, részecskék ütközése
Négyesimpulzus, impulzusmegmaradás
A nemrelativisztikus esethez hasonlón bevezetjük a részecskék négyesimpulzusát:
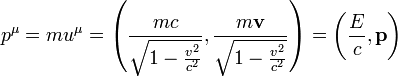
Az itt nem részletezett elméleti (Lagrange-féle) tárgyalásból következik, hogy a nulladik komponens a részecske energiája (a fénysebességgel osztva), a három térszerű komponens pedig a hármas impulzus. A fenti képleten egyértelműen látszik, hogy ezeknek az értéke természetesen nem egyezik meg a klasszikus mechanikában használt energiával és impulzussal (bár a fogalom hasonló), az hármas imulzusnál az eltérés a nevezőben levő gyökös kifejezés. Ha bevezetjük az 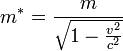 effektív tömeget (és az eredeti, eddig szereplő
effektív tömeget (és az eredeti, eddig szereplő 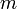 tömeget nyugalmi tömegnek hívjuk), akkor az így adódó
tömeget nyugalmi tömegnek hívjuk), akkor az így adódó 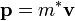 képlet alakja megegyezik a klasszikus esetben használt összefüggéssel, ezt szokás úgy értelmezni, hogy a részecskék tömege mozgás közben megnő. Ez az értelmezés bizonyos esetekben szemléletes, más esetekben viszont elbonyolíthatja a számolásokat (hiszen számon kell tartani, hogy
képlet alakja megegyezik a klasszikus esetben használt összefüggéssel, ezt szokás úgy értelmezni, hogy a részecskék tömege mozgás közben megnő. Ez az értelmezés bizonyos esetekben szemléletes, más esetekben viszont elbonyolíthatja a számolásokat (hiszen számon kell tartani, hogy 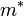 is változik, és például a deriválások elvégzésekor nem szabad elfelejteni a gyökös kifejezésben szereplő
is változik, és például a deriválások elvégzésekor nem szabad elfelejteni a gyökös kifejezésben szereplő 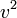 -et is deriválni, illetve vannak elméletek, ahol egy másfajta effektív tömeget kell bevezetni), így a továbbiakban ezt a jelölést nem használjuk, a képletekben szereplő
-et is deriválni, illetve vannak elméletek, ahol egy másfajta effektív tömeget kell bevezetni), így a továbbiakban ezt a jelölést nem használjuk, a képletekben szereplő 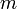 mindig a nyugalmi tömeget jelöli, aminek az értéke állandó, megelégszünk azzal, hogy a 4-es sebesség és -impulzusok közötti összefüggés alakja ugyanaz, mint klasszikus esetben (ott természetesen a nyugalmi tömeg szerepel). Természetesen, ha a részecske sebessége a fénysebességhez képest kicsi (a klasszikus határesetben), akkor a gyökös kifejezés értéke majdnem
mindig a nyugalmi tömeget jelöli, aminek az értéke állandó, megelégszünk azzal, hogy a 4-es sebesség és -impulzusok közötti összefüggés alakja ugyanaz, mint klasszikus esetben (ott természetesen a nyugalmi tömeg szerepel). Természetesen, ha a részecske sebessége a fénysebességhez képest kicsi (a klasszikus határesetben), akkor a gyökös kifejezés értéke majdnem 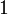 , így határesetben a klasszikus képletet kapjuk.
, így határesetben a klasszikus képletet kapjuk.
A négyesimpulzus abszolútértéknégyzete (kihasználva, hogy a négyessebességé 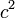 ):
):
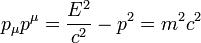
Ezt az összefüggést átalakítva, az energia és impulzus (illetve a sebesség) közötti összefüggéseket kapjuk:
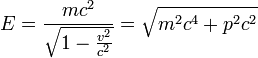
Álló részecskére a híres 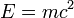 képlet adódik. Abban az esetben, ha a részecske sebessége a fénysebességhez képest nagyon kicsi, az energia sebességtől függését adó képletet sorbafejthetjük:
képlet adódik. Abban az esetben, ha a részecske sebessége a fénysebességhez képest nagyon kicsi, az energia sebességtől függését adó képletet sorbafejthetjük:
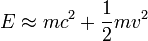
Az összeg első tagja az olyan reakciókban, amik nem járnak a részecskék átalakulásával, állandó, így klasszikusan nem mérhető, a második tag a klasszikus mechanikából ismert mozgási energia.
A klasszikus mechanika energia- és impulzusmegmaradási tételéhez hasonlóan a négyesimpulzus megmaradó mennyiség; egy zárt rendszer teljes négyesimpulzusa megmarad. Ez azt jelenti, hogyha egy rögzített inerciarendszerből nézünk egy eseményt, akkor a négyesimpulzus mindegyik komponense megmarad. Természetesen, ha áttérünk egy másik inerciarendszerbe, a négyesimpulzus komponenseit egy Lorentz-transzformációval kell áttranszformálni (így a komponensek transzformálódnak, egy rendszer energiája a különböző mozgó koordinátarendszerekből nézve nem ugyanaz), az viszont igaz, hogy a négyesimpulzus abszolútértéke (a részecske vagy rendszer nyugalmi tömege) minden inerciarendszerből nézve ugyanaz.
Részecskék ütközése
Ebben a szakaszban a négyesimpulzus megmaradásából következő összefüggéseket vizsgáljuk. Természetesen egy ilyen folyamat teljes leírásához ismernünk kellene a részecskék között ható kölcsönhatásokat, itt csak azt vizsgáljuk meg, hogy mi következik csak az impulzusmegmaradásból, a részecskék közötti kölcsönhatást csak az ütközési pont kis környezetére korlátozva (a részleteket elhanyagolva).
Rugalmas ütközésről akkor beszélhetünk, ha az ütközés után kijövő részecskék megegyeznek a bemenő részecskékkel (nem játszódik le például magreakció), így a nyugalmi tömegek nem változnak. (itt sok nagy képlet van a jegyzetemben, amiknek nincs igazán szemléletes jelentése)
Rugalmatlan ütközésnél a kijövő részecskék mások lehetnek (részecskék annihilálódhatnak, és új részecskék keletkezhetnek), így a nyugalmi tömegek is változnak. A legegyszerűbb eset az, amikor egy részecske elbomlik két másikra. Az eseményt a bomló részecske nyugalmi rendszeréből nézve, a kezdeti négyesimpulzus:
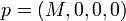
A bomlástermékek impulzusa:

A négyesimpulzus megmaradását felírva:
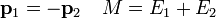
Legyen a bomlástermékek nyugalmi tömege 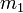 és
és 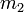 . A négyesimpulzus korábbi bevezetéséből látszik, hogy
. A négyesimpulzus korábbi bevezetéséből látszik, hogy 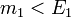 és
és  , ezt a négyesimpulzus megmaradásával összevetve látszik, hogy a bomlás feltétele, hogy a
, ezt a négyesimpulzus megmaradásával összevetve látszik, hogy a bomlás feltétele, hogy a 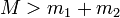 egyenlőtlenség teljesüljön, ami azt is jelenti, hogy a klasszikus értelemben vett tömeg nem marad meg, úgy lehet értelmezni, hogy egy része a bomlástermékek mozgási energiájává alakul (egy atomerőműben ebből keletkezik a hő, amit felhasználnak). A hármas impulzus megmaradására vonatkozó egyenletet négyzetre emelve és a
egyenlőtlenség teljesüljön, ami azt is jelenti, hogy a klasszikus értelemben vett tömeg nem marad meg, úgy lehet értelmezni, hogy egy része a bomlástermékek mozgási energiájává alakul (egy atomerőműben ebből keletkezik a hő, amit felhasználnak). A hármas impulzus megmaradására vonatkozó egyenletet négyzetre emelve és a 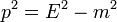 egyenlőséget kihasználva az
egyenlőséget kihasználva az 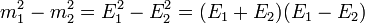 összefüggést kapjuk, ahonnan az energiamegmaradásra vonatkozó egyenlőség felhasználásával az energiák kifejezhetőek:
összefüggést kapjuk, ahonnan az energiamegmaradásra vonatkozó egyenlőség felhasználásával az energiák kifejezhetőek:
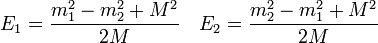
Ez a tömegközépponti rendszerben érvényes, ha a bomló részecske a labor koordinátarendszeréhez képest mozgott, akkor egy Lorentz-transzformáció kell végezni, és a végeredményben az energia a szórási szögtől is függ.
Ennek a fordított folyamata az, amikor két részecske ütközik, és arra vagyunk kíváncsiak, hogy mekkora tömegű részecske tud maximálisan keletkezni. Érdemes kihasználni, hogy a rendszer összes impulzusmomentumának az abszlútértéknégyzete a rendszer nyugalmi tömegét adja: 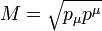 . Két azonos energiájú nyalábot összeütköztetve, az így elérhető maximális tömeg a nyalábenergia kétszerese. Ezzel szemben, ha egy álló (
. Két azonos energiájú nyalábot összeütköztetve, az így elérhető maximális tömeg a nyalábenergia kétszerese. Ezzel szemben, ha egy álló (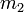 tömegű részecskékből álló) céltárgyra lövünk egy
tömegű részecskékből álló) céltárgyra lövünk egy 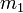 tömegű,
tömegű, 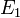 energiájú részecskékből álló nyalábot, az összimpulzus (két részecske ütközése után):
energiájú részecskékből álló nyalábot, az összimpulzus (két részecske ütközése után): 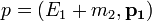 . Kihasználva, hogy
. Kihasználva, hogy  adódik, hogy:
adódik, hogy:
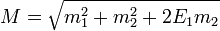 . Ha a kísérleteket
. Ha a kísérleteket 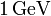 tömegű protonokkal végezzük,
tömegű protonokkal végezzük, 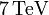 nyalábenergiával, akkor az álló céltárgyas esetben
nyalábenergiával, akkor az álló céltárgyas esetben 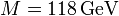 adódik, ami kevesebb, mint a százada a két nyaláb ütköztetésénél elérhető
adódik, ami kevesebb, mint a százada a két nyaláb ütköztetésénél elérhető 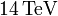 -nek.
-nek.