VélFiz 2.tétel
2. tétel: Brown-mozgás: Langevin levezetése
Alapfeltevések
- A részecskék egymástól függetlenül mozognak.
-
 << megfigyelési idő minimuma (ezen túl a mozgás az előzőektől függetlennek tekinthető)
<< megfigyelési idő minimuma (ezen túl a mozgás az előzőektől függetlennek tekinthető) - Az elmozdulásnak van egy valószínűségi eloszlása. A mozgás leírható valószínűségi alapon.
Langevin levezetése "fizikaibb", Einsteinnél ugyanis nem lehet tudni, hogy a részecskével konkrétan mi történik. A Langevin-féle leírás ebből a szempontból szemléletesebb.
Langevin: részecskék lökdösik a megfigyelt részecskét, a mozgás a hőmérsékleti fluktuációból jön, tehát egy véletlen erő hozza létre.
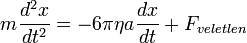
Ahol a jobb oldal első tagja a fékezőerő, ami egy determinisztikus erő (a a sugár, 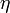 a viszkozitás (angolul, magyarul) amit kísérlettel lehet mérni).
a viszkozitás (angolul, magyarul) amit kísérlettel lehet mérni).
Célunk, hogy a fenti egyenletből kiindulva megkapjuk az Einstein-féle leírásnál eredményül kapott 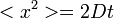 összefüggést.
összefüggést.
A fenit egyenlet mindkét oldalát szorozzuk x-szel
Felhasznált összefüggések: 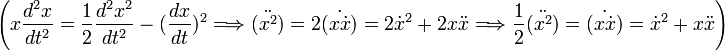
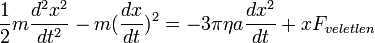
A véletlen erő átlagos munkája nulla, hiszen ha >0 lenne, a részecske egyre gyorsulna és elszállna, ha <0 lenne, akkor megállna, de a kísérletekből látszik, hogy nem áll meg. A folyadék (vagy gáz) egyensúlyban van egy adott hőmérsékleten (és a vizsgált részecske is ott van, csak kicsit nagyobb), ezért:
Átlagot vesszük: 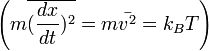
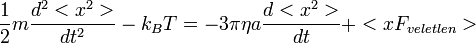
Vezessük be a 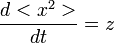 új változót. Ekkor a fenti egyenlet a következőképpen módosul:
új változót. Ekkor a fenti egyenlet a következőképpen módosul:
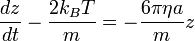
A fenti egyenlet megoldása a homogén megoldás és a partikuláris megoldás összege:
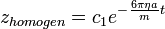
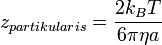 --> z-t konstansnak tételeztük fel
--> z-t konstansnak tételeztük fel
Ekkor z eredeti értékét visszaírva és a két megoldást összeadva a következő eredményt kapjuk:
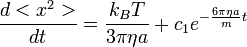
Ám 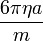
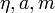 konkrét értékeire és
konkrét értékeire és 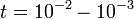 -ra ez egy nagyon nagy szám, emiatt
-ra ez egy nagyon nagy szám, emiatt 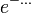 nagyon kicsi.
nagyon kicsi.
Például:
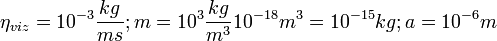
Ekkor: 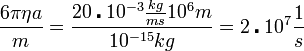
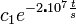 bármely rezonábilis t-re nullát ad, tehát elhagyható. Ekkor:
bármely rezonábilis t-re nullát ad, tehát elhagyható. Ekkor:
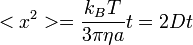
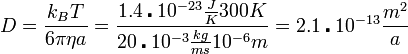
A fenti képlet alapján becslés (úgy általában):