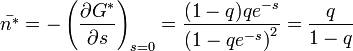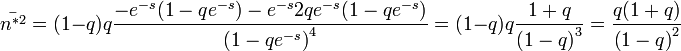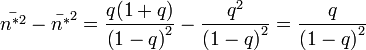VélFiz 5.tétel
5. tétel: Generátor függvények: Sorbanállási problémák
Végtelen sok állapot esetén (Master-egyenlet végtelen állapottérrel) a Generátor-függvények módszerét érdemes használni.
Sorbanállási problémák
Egy fizikai pl.: atom abszorpció - kirakódások és elpárolgások...
Jelölések:
-
 : bejöveteli ráta
: bejöveteli ráta -
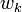 : kimeneti, feldolgozási ráta
: kimeneti, feldolgozási ráta
Stac. állapotot jellemző mennyiségek:
-
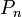 : milyen valószínűséggel van n vásárló a pénztárnál?
: milyen valószínűséggel van n vásárló a pénztárnál? -
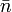 : átlagosan mennyien állnak a pénztárnál?
: átlagosan mennyien állnak a pénztárnál? -
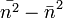 : Fluktuáció
: Fluktuáció
P változásának valószínűsége: (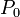 külön eset, hiszen nincs
külön eset, hiszen nincs 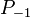 .)
.)
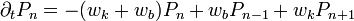
- jobb oldal 1.tagja:
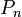 állapotból való kilépés bejövetel vagy kimenetel által
állapotból való kilépés bejövetel vagy kimenetel által - 2.tag:
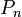 állapotba lépés bejövetellel;
állapotba lépés bejövetellel; - 3.tag:
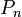 állapotba lépés kimenetellel;
állapotba lépés kimenetellel;
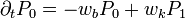
Momentum generátor függvény bevezetése:
(Az eloszlásfüggvény momentumait generálja)
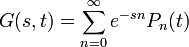
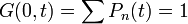
1. momentum: 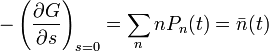
2. momentum: 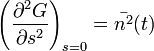
Ez utóbbit felhasználva: ![\bar{n^{2}}-\bar{n}^{2}=\left[\left(\frac{\partial^{2}G}{\partial s^{2}}\right)-\left(\frac{\partial G}{\partial s}\right)^{2}\right]_{s=0}](/images/math/e/3/3/e33f0f6007b8e7fdd09afe421a7372b4.png)
Vezessük be a következő jelölést: 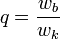 . Stacionáris megoldás van, ha
. Stacionáris megoldás van, ha 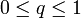 .
.
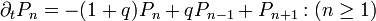
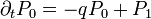
Így G időbeli változása:
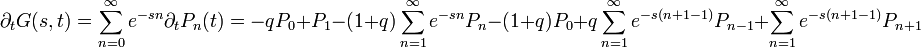 , ahol
, ahol
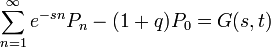
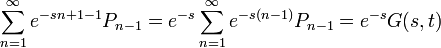
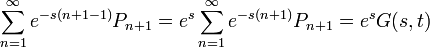
- és
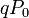 -ak kiejtik egymást
-ak kiejtik egymást
Ez utóbbiakkal:
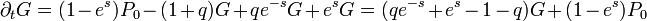
Stacionárius állapot esetén:
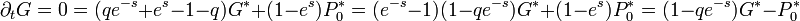 , mivel
, mivel 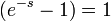
Ebből átrendezéssel kapjuk a stacionárius generátor-függvényt:
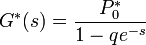
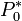 a normálásból több féle képpen is kifejezhető, az eredmény:
a normálásból több féle képpen is kifejezhető, az eredmény:
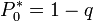
Az előbbiek alapján az egyensúlyi generátor függvény:
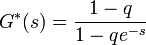
Stacionárius esetben a momentumok:
A "matematikus" leírást kihagytam, remélem nem gond. Cz
A kumuláns Generátor-függvény bevezetése: 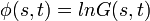
A kumulánsok:
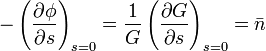
![\left(\frac{\partial^{2}\phi}{\partial s^{2}}\right)_{s=0}=\left[\frac{1}{G}\frac{\partial^{2}G}{\partial s^{2}}-\frac{1}{G^{2}}\left(\frac{\partial G}{\partial s}\right)^{2}\right]_{s=0}=\bar{n^{2}}-\bar{n}^{2}](/images/math/4/3/1/4313d5ed83c169d5a2a555ab86eaea13.png)
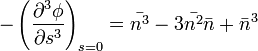 - a harmadik kumuláns megadja, mennyire nem szimmetrikus a függvény.
- a harmadik kumuláns megadja, mennyire nem szimmetrikus a függvény.- A 4. kumuláns megadja, hogy a függvény a Gauss-hoz képest mennyire keskeny
Gauss-függvény elestében az első két kumuláns nem nulla, de a többi utánuk 0:
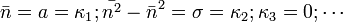
Generátor-függvény Fourier-transzformálva: 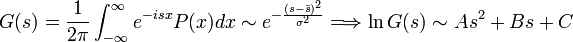
Gauss-on kívül nincs másik olyan függvény, hogy valamettől 0-k a kumulánsai, mert visszafelé transzformálva P-re negatív értéket kapnánk.