„Csega/Tomography” változatai közötti eltérés
| (Egy közbenső módosítás ugyanattól a szerkesztőtől nincs mutatva) | |||
| 9. sor: | 9. sor: | ||
Sok esetben szükséges lehet a tér különböző részein mérhető emisszivitás, <math>G \left(r, \theta \right)</math>, ez pedig a nyers adatok '''tomografikus inverziójával''' számolható ki. Ennek megvalósítására több különböző technika is létezik. A leghasznosabb módszer az invertált adatok leírására a Cormack által bevezetett, mely a Zernicke polinomok <math>\left( R_{ml} \right)</math> bővítésén alapul: | Sok esetben szükséges lehet a tér különböző részein mérhető emisszivitás, <math>G \left(r, \theta \right)</math>, ez pedig a nyers adatok '''tomografikus inverziójával''' számolható ki. Ennek megvalósítására több különböző technika is létezik. A leghasznosabb módszer az invertált adatok leírására a Cormack által bevezetett, mely a Zernicke polinomok <math>\left( R_{ml} \right)</math> bővítésén alapul: | ||
| − | <math>G(r\phi) = \sum_{lm} \left( \right)</math> | + | <math>G(r\phi) = \sum_{lm} \left( A_{ml}^s sin(m \theta)+A_{ml}^c cos(m \theta)\right) R_{ml}(r)</math>. |
| + | |||
| + | Ahol a Zernicke polinomok a következőképpen írhatók fel: | ||
| + | |||
| + | <math>R_{ml}(r) \equiv \sum_{s=0}^l \frac{(-l)^s (m+2l-s)!}{s! (m+l-s)! (l-s)!}r^{m+2l-2s}</math>. | ||
| + | |||
| + | A megfigyelt (line of sight) adat a következőképpen fejezhető ki: | ||
| + | |||
| + | <math>F(p,\chi) = \sum_{lm} \left( A_{ml}^s sin(m \chi) + A_{ml}^c cos(m \chi)\right) S_{ml}(p)</math>, | ||
| + | |||
| + | ahol <math>S_{ml}(p) = \frac{2sin(m+2l+1)cos^{-1}(p)}{m+2l+1}</math> és <math>\chi</math> a detektor szöge (lásd a fenti ábrát). | ||
| + | |||
| + | [[Csega/Plazmafizika|<<<Vissza Csega plazmafizika lapjára]] | ||
== Hivatkozások == | == Hivatkozások == | ||
<references/> | <references/> | ||
A lap jelenlegi, 2012. július 30., 14:54-kori változata
A megfigyelt lágy röntgensugarak tulajdonképpen integrálok a látóirány mentén[1]. Az intenzitás a következő integrállal adható meg:
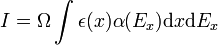 ,
,
ahol 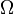 a detektor térszöge,
a detektor térszöge, 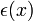 a plazma emisszivitása (sugárzási képessége),
a plazma emisszivitása (sugárzási képessége), 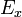 a röntgensugár energiája,
a röntgensugár energiája, 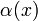 pedig a röntgenszűrő átviteli tényezője (transmission coefficient). A geometria és a koordináták az alábbi ábrán tekinthetők meg.
pedig a röntgenszűrő átviteli tényezője (transmission coefficient). A geometria és a koordináták az alábbi ábrán tekinthetők meg.
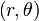 és a detektor koordináták
és a detektor koordináták 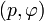 közötti kapcsolat.
közötti kapcsolat.Sok esetben szükséges lehet a tér különböző részein mérhető emisszivitás, 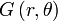 , ez pedig a nyers adatok tomografikus inverziójával számolható ki. Ennek megvalósítására több különböző technika is létezik. A leghasznosabb módszer az invertált adatok leírására a Cormack által bevezetett, mely a Zernicke polinomok
, ez pedig a nyers adatok tomografikus inverziójával számolható ki. Ennek megvalósítására több különböző technika is létezik. A leghasznosabb módszer az invertált adatok leírására a Cormack által bevezetett, mely a Zernicke polinomok 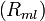 bővítésén alapul:
bővítésén alapul:
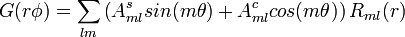 .
.
Ahol a Zernicke polinomok a következőképpen írhatók fel:
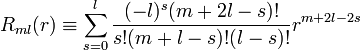 .
.
A megfigyelt (line of sight) adat a következőképpen fejezhető ki:
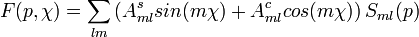 ,
,
ahol 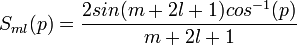 és
és 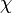 a detektor szöge (lásd a fenti ábrát).
a detektor szöge (lásd a fenti ábrát).
<<<Vissza Csega plazmafizika lapjára
Hivatkozások
- ↑ Wesson - Tokamaks (3. kiadás, 544. oldal, a 2. kiadásban ugyanez az 513. oldalon található)