„Relativisztikus kvantummechanika” változatai közötti eltérés
(Új oldal, tartalma: „Ebben a részben <math>c = 1</math> ===A Klein-Gordon egyenlet=== Legyen <math>\Psi (t,\mathbf{x})</math> egy részecske hullámfüggvénye, mint egy inerciarendszerbeli…”) |
a |
||
| 1. sor: | 1. sor: | ||
Ebben a részben <math>c = 1</math> | Ebben a részben <math>c = 1</math> | ||
| − | + | ==A Klein-Gordon egyenlet== | |
Legyen <math>\Psi (t,\mathbf{x})</math> egy részecske hullámfüggvénye, mint egy inerciarendszerbeli tér- és időkoordináták skalárfüggvénye. Erre szeretnénk felírni egy kovariáns egyenletet, ami összhangban van a relativitáselmélettel. Ehhez induljunk ki a <math>E^2 = p^2 + m^2</math> egyenletből, és helyettesítsük a fizikai mennyiségeket a klasszikus kvantummechanikából ismert operátoraikkal. Az impulzus operátora: <math>\mathbf{p} \sim -i \hbar \nabla</math>, az energiát az időderiváltnak feleltethetjük meg: <math>E \sim i \hbar \frac{\partial}{\partial t}</math>, a tömeg pedig itt is egy állandó. Így a fenti egyenletnek megfelelő operátorokat a hullámfüggvényre hattatva a következő egyenletet kapjuk: | Legyen <math>\Psi (t,\mathbf{x})</math> egy részecske hullámfüggvénye, mint egy inerciarendszerbeli tér- és időkoordináták skalárfüggvénye. Erre szeretnénk felírni egy kovariáns egyenletet, ami összhangban van a relativitáselmélettel. Ehhez induljunk ki a <math>E^2 = p^2 + m^2</math> egyenletből, és helyettesítsük a fizikai mennyiségeket a klasszikus kvantummechanikából ismert operátoraikkal. Az impulzus operátora: <math>\mathbf{p} \sim -i \hbar \nabla</math>, az energiát az időderiváltnak feleltethetjük meg: <math>E \sim i \hbar \frac{\partial}{\partial t}</math>, a tömeg pedig itt is egy állandó. Így a fenti egyenletnek megfelelő operátorokat a hullámfüggvényre hattatva a következő egyenletet kapjuk: | ||
| 77. sor: | 77. sor: | ||
Az egyik esetben a töltéssűrűség pozitív, a másikban negatív. Ezt úgy lehet értelmezni, hogy a <math>\Psi_{+}</math> megoldás <math>+e</math> töltésű, a <math>\Psi_{-}</math> megoldás <math>-e</math> töltésű részecskéket ír le. | Az egyik esetben a töltéssűrűség pozitív, a másikban negatív. Ezt úgy lehet értelmezni, hogy a <math>\Psi_{+}</math> megoldás <math>+e</math> töltésű, a <math>\Psi_{-}</math> megoldás <math>-e</math> töltésű részecskéket ír le. | ||
| − | + | ==A Dirac-egyenlet== | |
Szeretnénk egy, a Schrödinger-egyenlethez hasonló alakú (időben elsőrendű), de a relativitáselmélettel összhangban levő egyenletet bevezetni. A Schrödinger-egyenlet ismert alakja: | Szeretnénk egy, a Schrödinger-egyenlethez hasonló alakú (időben elsőrendű), de a relativitáselmélettel összhangban levő egyenletet bevezetni. A Schrödinger-egyenlet ismert alakja: | ||
A lap 2009. szeptember 13., 13:04-kori változata
Ebben a részben 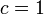
A Klein-Gordon egyenlet
Legyen 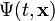 egy részecske hullámfüggvénye, mint egy inerciarendszerbeli tér- és időkoordináták skalárfüggvénye. Erre szeretnénk felírni egy kovariáns egyenletet, ami összhangban van a relativitáselmélettel. Ehhez induljunk ki a
egy részecske hullámfüggvénye, mint egy inerciarendszerbeli tér- és időkoordináták skalárfüggvénye. Erre szeretnénk felírni egy kovariáns egyenletet, ami összhangban van a relativitáselmélettel. Ehhez induljunk ki a 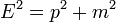 egyenletből, és helyettesítsük a fizikai mennyiségeket a klasszikus kvantummechanikából ismert operátoraikkal. Az impulzus operátora:
egyenletből, és helyettesítsük a fizikai mennyiségeket a klasszikus kvantummechanikából ismert operátoraikkal. Az impulzus operátora: 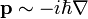 , az energiát az időderiváltnak feleltethetjük meg:
, az energiát az időderiváltnak feleltethetjük meg: 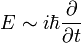 , a tömeg pedig itt is egy állandó. Így a fenti egyenletnek megfelelő operátorokat a hullámfüggvényre hattatva a következő egyenletet kapjuk:
, a tömeg pedig itt is egy állandó. Így a fenti egyenletnek megfelelő operátorokat a hullámfüggvényre hattatva a következő egyenletet kapjuk:
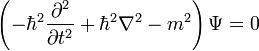
Ez a Klein-Gordon egyenlet. Ezt felírhatjuk négyesvektoros alakban is. Az energia és impulzus közötti összefüggés (diszperziós reláció) négyesvektorosan: 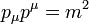 . Az előző megfeleltetés operátoroknak ekkor:
. Az előző megfeleltetés operátoroknak ekkor: 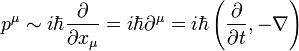 . A Klein-Gordon egyenlet ilyen alakban:
. A Klein-Gordon egyenlet ilyen alakban:
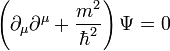
A Klein-Gordon egyenlet síkhullám megoldásait egyszerűen felírhatjuk:
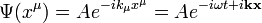
Ezt az egyenletbe behelyettesítve láthatjuk, hogy kielégíti azt, ha teljesül a 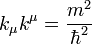 feltétel. Ez azt jelenti, hogy a
feltétel. Ez azt jelenti, hogy a 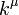 négyesvektor komponenseiből csak 3 független. Legyyenek a komponensek:
négyesvektor komponenseiből csak 3 független. Legyyenek a komponensek: 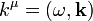 , így ezekre a
, így ezekre a 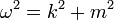 diszperziós reláció adódik. A kvantummechanikában szokásos értelmezés szerint az energia (ez az időderiválás operátor sajátértéke is)
diszperziós reláció adódik. A kvantummechanikában szokásos értelmezés szerint az energia (ez az időderiválás operátor sajátértéke is) 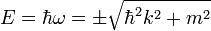 . Formálisan a pozitív energiás megoldás mellett van egy negatív energiájú is (ez jelenti majd az antirészecskéket).
. Formálisan a pozitív energiás megoldás mellett van egy negatív energiájú is (ez jelenti majd az antirészecskéket).
Eddig még nem beszéltünk arról, hogy milyen részecskék leírására alkalmas a Klein-Gordon egyenlet, felmerül a kérdés, hogy ez az egyenlet alkalmas-e a Schrödinger egyenlet relativisztikus általánosításaként. Elvileg ezzel az egyenlettel 0 spinű részecskéket lehetne leírni, a valóságban azonban nincs olyan elemi részecske, amit csak a Klein-Gordon egyenlet írna le (a fotonokra felírható hullámegyenletek hasonlóak, de ott nem egy skalármező, hanem a potenciálokból álló négyesvektor komponensei szerepelnek). Ennek ellenére érdemes megvizsgálni, hogyha lennének ilyen részecskék, akkor milyen tulajdonságokkal rendelkeznének. A Schrödinger-egyenletnél a hullámfüggvény abszolútértékének négyzete megtalálási valószínűségsűrűségként volt értelmezhető. Kérdéses, hogy itt lehet-e ehhez hasonló megállapításokat tenni. Ehhez írjuk fel a Klein-Gordon egyenletet és a komplex konjugáltját:
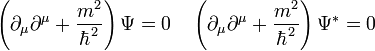
Szorozzuk meg az eredeti egyenletet (balról) 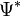 -al, a komplex konjugált egyenletet
-al, a komplex konjugált egyenletet 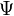 -vel, és vonjuk ki a kettőt egymásból. Az eredmény:
-vel, és vonjuk ki a kettőt egymásból. Az eredmény:
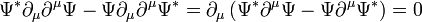
Azt kaptuk, hogy egy négyesvektor divergenciája 0. Ez lehetőséget ad egy négyesáram bevezetésére, amire egy megmaradási tétel (kontinuitási egyenlet) írható fel. Legyen:
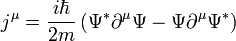
Ekkor fennáll, hogy 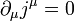 . A komponenseket
. A komponenseket 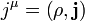 formában írva ez egy kontinuitási egyenlet jelent:
formában írva ez egy kontinuitási egyenlet jelent:
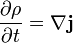
Az egész térre integrálva azt kapjuk, hogy a 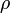 sűrűség integrálja állandó:
sűrűség integrálja állandó:
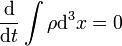
Ez alapján azt lehetne mondani, hogy 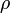 a Schrödinger egyenletnél bevezethető valószínűségsűrűséghez hasonlóan viselkedik, ennek ellenére nem lehet valószínűségsűrűségként értelmezni, mert a Schrödinger-egyenletnél használt abszolútértéknégyzettel szemben
a Schrödinger egyenletnél bevezethető valószínűségsűrűséghez hasonlóan viselkedik, ennek ellenére nem lehet valószínűségsűrűségként értelmezni, mert a Schrödinger-egyenletnél használt abszolútértéknégyzettel szemben 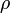 értéke nem csak pozitív lehet, hanem negatív is. Ez abból következik, hogy a Klein-Gordon egyenlet időben másodrendű, így kezdőfeltételként
értéke nem csak pozitív lehet, hanem negatív is. Ez abból következik, hogy a Klein-Gordon egyenlet időben másodrendű, így kezdőfeltételként 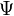 -t és az idő szerinti deriváltját tetszőlegesen lehet megválasztani, úgy is, hogy
-t és az idő szerinti deriváltját tetszőlegesen lehet megválasztani, úgy is, hogy 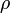 egyes helyeken negatív legyen.
egyes helyeken negatív legyen.
Így a Klein-Gordon megoldásainak nem lehet a Schrödinger-egyenletnél megszokott valószínűségi értelmezést adni. Abban az esetben viszont, ha töltött részecskékről van szó, egy töltés áramsűrűséget lehet bevezetni. Legyen ekkor:
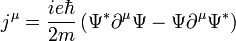
Az előző definícióhoz képest az egyetlen eltérés a részecskék töltésegységét jelentő  szorzó, így
szorzó, így 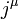 négyes áramsűrűségként értelmezhető (a kontinuitási egyenlet ugyanúgy teljesül rá). A nulladik komponenes a töltéssűrűség:
négyes áramsűrűségként értelmezhető (a kontinuitási egyenlet ugyanúgy teljesül rá). A nulladik komponenes a töltéssűrűség:
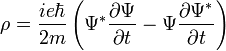
A térszerű komponensek a hármas áramsűrűséget adják:
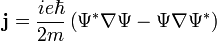
Az össztöltés megmarad:
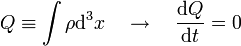
Ezzel szemben 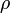 értéke egy adott pontban tetszőlegesen változhat, lehet pozitív és negatív is. Ez azt jelenti, hogy a Klein-Gordon egyenlettel nem lehet egy rögzített (pozitív vagy negatív) töltésű részecskét leírni, az időfejlődés során megjelenhetnek ellentétes töltésű tartományok, ennek magyarázata az, hogy minden részecskének létezik ellentétes töltésű antirészecskéje, és a részecskék és antirészecskék száma nem marad meg, csak az össztöltés, keletkezhetnek és annihilálódhatnak részecske-antirészecske párok. Ennek a teljes leírására azonban a Klein-Gordon egyenlet jelenlegi formája nem alkalmas, el kell végezni a
értéke egy adott pontban tetszőlegesen változhat, lehet pozitív és negatív is. Ez azt jelenti, hogy a Klein-Gordon egyenlettel nem lehet egy rögzített (pozitív vagy negatív) töltésű részecskét leírni, az időfejlődés során megjelenhetnek ellentétes töltésű tartományok, ennek magyarázata az, hogy minden részecskének létezik ellentétes töltésű antirészecskéje, és a részecskék és antirészecskék száma nem marad meg, csak az össztöltés, keletkezhetnek és annihilálódhatnak részecske-antirészecske párok. Ennek a teljes leírására azonban a Klein-Gordon egyenlet jelenlegi formája nem alkalmas, el kell végezni a 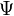 tér második kvantálását. Ezt itt nem tesszük meg, az antirészecskék jelenlétét viszont a síkhullám megoldásokon is tudjuk egyszerűen szemléltetni. Ehhez írjuk fel az előbbi síkhullám megoldást (a szokásos
tér második kvantálását. Ezt itt nem tesszük meg, az antirészecskék jelenlétét viszont a síkhullám megoldásokon is tudjuk egyszerűen szemléltetni. Ehhez írjuk fel az előbbi síkhullám megoldást (a szokásos 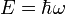 és
és 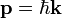 jelöléseket használva):
jelöléseket használva):
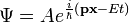
Itt 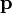 tetszőleges (hármas) vektor, és érvényes az
tetszőleges (hármas) vektor, és érvényes az 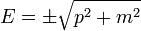 diszperziós reláció. Legyen a pozitív megoldás
diszperziós reláció. Legyen a pozitív megoldás 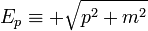 , így
, így 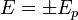 , a különböző előjelhez tartozó megoldások külön felírva:
, a különböző előjelhez tartozó megoldások külön felírva:

Az ezekből számolt töltéssűrűségek (a deriválást elvégezve):

Az egyik esetben a töltéssűrűség pozitív, a másikban negatív. Ezt úgy lehet értelmezni, hogy a 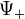 megoldás
megoldás 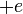 töltésű, a
töltésű, a 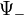 megoldás
megoldás 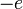 töltésű részecskéket ír le.
töltésű részecskéket ír le.
A Dirac-egyenlet
Szeretnénk egy, a Schrödinger-egyenlethez hasonló alakú (időben elsőrendű), de a relativitáselmélettel összhangban levő egyenletet bevezetni. A Schrödinger-egyenlet ismert alakja:
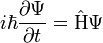
Szeretnénk, ha a Hamilton-operátor összhangban lenne a relativitáselmélet 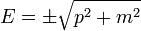 összefüggésével. Tegyük fel, hogy létezik egy ilyen operátor, ami előáll az impulzusok (térszerinti deriváltak) és a tömeg (mint számmal szorzás) lineárkombinációjaként, és a négyzetére teljesül a relativisztikus energia-impulzus összefüggés (a továbbiakban a latin betűs indexek a térszerű koordinátákat jelölik:
összefüggésével. Tegyük fel, hogy létezik egy ilyen operátor, ami előáll az impulzusok (térszerinti deriváltak) és a tömeg (mint számmal szorzás) lineárkombinációjaként, és a négyzetére teljesül a relativisztikus energia-impulzus összefüggés (a továbbiakban a latin betűs indexek a térszerű koordinátákat jelölik: 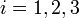 , rájuk is vonatkozik a kétszer előforduló indexre automatikus összegzés szabálya):
, rájuk is vonatkozik a kétszer előforduló indexre automatikus összegzés szabálya):

A fenti feltételeknek nincs megoldása abban az esetben, ha az 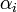 és
és 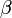 együtthatók számok, így keressük úgy a megoldást, hogy a
együtthatók számok, így keressük úgy a megoldást, hogy a 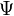 hullámfüggvény több komponensű (oszlopvektor) és az együtthatók mátrixok. Így a feltételeink:
hullámfüggvény több komponensű (oszlopvektor) és az együtthatók mátrixok. Így a feltételeink:
- Legyen
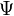 egy
egy 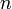 komponensű vektor, a komponenseit jelölje
komponensű vektor, a komponenseit jelölje 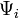
- Legyen a
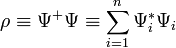 mennyiség egy megmaradó 4-es áram nulladik komponense
mennyiség egy megmaradó 4-es áram nulladik komponense
- Teljesüljön a relativisztikus
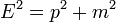 összefüggés. Ez azt jelenti, hogy
összefüggés. Ez azt jelenti, hogy 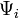 minden komponense kielégíti a Klein-Gordon egyenletet
minden komponense kielégíti a Klein-Gordon egyenletet
- Legyen az egyenlet kovariáns, azaz teljesítse azt a feltételt, hogy mindkét oldalán a Lorentz-transzformációk szempontjából ugyanúgy transzformálódó mennyiségek szerepelnek
Megmutatható, hogy ezek a feltételek az együtthatómátrixokra a következő egyenleteket adják:
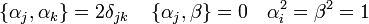
A kapcsos zárójelek az antikommutátorokat jelentik. Ezeket az egyenleteket legkevesebb 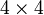 -es mátrixokkal lehet kielégíteni, léteznek magasabb dimenziójú megoldások is, mi a továbbiakban csak az
-es mátrixokkal lehet kielégíteni, léteznek magasabb dimenziójú megoldások is, mi a továbbiakban csak az 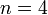 esettel foglalkozunk. Ebben az esetben a megoldás (igazából több megoldás lehetséges, de ezek nem függetlenek egymástól, így elég csak egyet vizsgálni):
esettel foglalkozunk. Ebben az esetben a megoldás (igazából több megoldás lehetséges, de ezek nem függetlenek egymástól, így elég csak egyet vizsgálni):
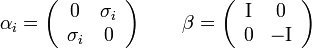
Itt 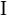 a
a 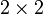 -es egységmátrix, a
-es egységmátrix, a 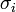 mátrixok a Pauli-mátrixok. A komponensek kiírva:
mátrixok a Pauli-mátrixok. A komponensek kiírva:
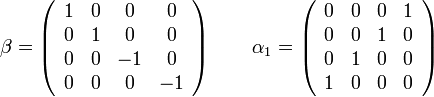
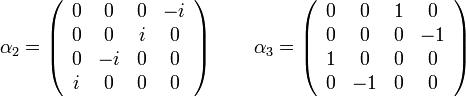
A 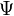 hullámfüggvény pedig egy négy komponensű vektor lesz. Nagyon fontos megjegyeznünk, hogy
hullámfüggvény pedig egy négy komponensű vektor lesz. Nagyon fontos megjegyeznünk, hogy 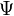 nem négyesvektor (a relativitáselméletben bevezetett módon), a komponenseit nem lehet a négyesvektorokra ható Lorentz-mátrixokkal transzformálni, matematikailag
nem négyesvektor (a relativitáselméletben bevezetett módon), a komponenseit nem lehet a négyesvektorokra ható Lorentz-mátrixokkal transzformálni, matematikailag 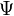 egy másik tér eleme. A továbbiakban az együtthatómátrixok és
egy másik tér eleme. A továbbiakban az együtthatómátrixok és 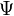 komponenseinek az indexeit általában elhagyjuk, azok között a mátrixalgebrában szokásos műveletek érvényesek. Az
komponenseinek az indexeit általában elhagyjuk, azok között a mátrixalgebrában szokásos műveletek érvényesek. Az 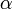 mátrixok indexei a mátrix sorszámát jelentik. Egyes esetekben nehéz számontartani a különböző fajta vektorok komponenseit, a lényeg az, hogy a differenciáloperátorok
mátrixok indexei a mátrix sorszámát jelentik. Egyes esetekben nehéz számontartani a különböző fajta vektorok komponenseit, a lényeg az, hogy a differenciáloperátorok 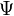 minden komponensére külön hatnak, egy együtthatómátrix pedig a mátrixszorzás szabályai szerint hat. A Dirac-egyenlet így felírva:
minden komponensére külön hatnak, egy együtthatómátrix pedig a mátrixszorzás szabályai szerint hat. A Dirac-egyenlet így felírva:
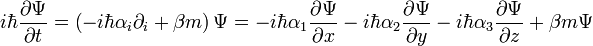
A jobboldali összeg minden tagjában a deriválás 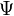 minden komponensére külön hat, majd az
minden komponensére külön hat, majd az 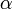 mátrixokkal szorzás a komponensek között hat a szokásos mátrixszorzási szabályok szerint.
mátrixokkal szorzás a komponensek között hat a szokásos mátrixszorzási szabályok szerint.