„Adatelemzés: ARCH, GARCH folyamatok” változatai közötti eltérés
(→Állítás: y_t korrelálatlan) |
(→ARCH, GARCH modellek) |
||
| 7. sor: | 7. sor: | ||
A legegyszerűbb ARCH modell az ARCH(1) modell: | A legegyszerűbb ARCH modell az ARCH(1) modell: | ||
| − | <math>y_t = \sigma_t \epsilon_t </math> (1) | + | <math>y_t = \sigma_t \epsilon_t</math> (1) |
<math>\sigma_t^2 = \alpha_0 + \alpha_1 y_{t-1}^2</math> (2) | <math>\sigma_t^2 = \alpha_0 + \alpha_1 y_{t-1}^2</math> (2) | ||
A lap 2011. június 7., 17:08-kori változata
Tartalomjegyzék
ARCH, GARCH modellek
- ARCH: autoregressive conditionally heteroscedastic; időben változó volatilitás (szórás, variancia) – mivel gazdasági idősorokra szokták alkalmazni, a volatilitás a használt kifejezés
- GARCH: generalized ARCH
A legegyszerűbb ARCH modell az ARCH(1) modell:
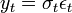 (1)
(1)
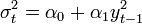 (2)
(2)
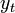 az idősor értéke t-ben,
az idősor értéke t-ben, 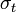 a szórás t-ben,
a szórás t-ben, 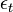 standard normál eloszlásból származó zaj,
standard normál eloszlásból származó zaj, 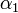 legyen nemnegatív.
legyen nemnegatív.
A 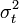 -re AR modellt írtunk fel.
-re AR modellt írtunk fel.
Miért is kell feltételes eloszlásról beszélni (ar conditionally h)? Ha az idősor stacionárius lenne, vagyis az összes elem azonos eloszlásból származna, egy későbbi érték eloszlása megegyezne a hosszú távú, feltétel nélküli eloszlással. A nem stacionárius idősorokra időben változhat a szórás, ezt ha figyelembe vesszük, akkor kapjuk a feltételes eloszlást.
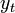 feltételes eloszlása gaussi:
feltételes eloszlása gaussi: 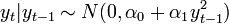
Az (1) és (2) egyenleteket 0-ra rendezve, egyenlővé téve, majd átrendezve a következőt kapjuk:
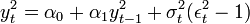
Ez egy nem-gaussi AR(1) modell az 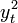 -re felírva.
-re felírva.
Állítás: 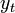 átlaga 0
átlaga 0
Biz.: legyen 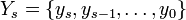 , ekkor, mivel
, ekkor, mivel 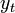 csak
csak  -től függ, az pedig egy nulla átlagú gauss:
-től függ, az pedig egy nulla átlagú gauss:
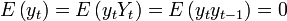
Állítás: 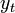 korrelálatlan
korrelálatlan
Bizonyítás:
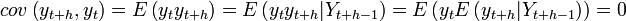 , ha
, ha 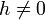
Kiszámolhatjuk 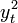 és
és  átlagát (az első könnyű, csak az AR modell képletét alkalmazzuk):
átlagát (az első könnyű, csak az AR modell képletét alkalmazzuk):
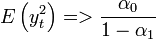
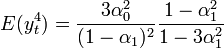
Ez a két érték a kurtózis kiszámolásához kellett:
![\kappa = \frac{E\left(y_t^4\right)}{\left[E\left(y_t^2\right)\right]^2} = 3\frac{1-\alpha_1^2}{1-3\alpha_1^2}](/images/math/b/4/5/b4554626545fea4d6466aa552dddb80e.png)
Ha a nevező pozitív, akkor ez mindig nagyobb lesz 3-nál (3 a normál eloszlás kurtózisa), vagyis ez egy vastag farkú (fat tail) eloszlás lesz.
ARCH(1) kiterjesztése ARCH(m)-re
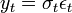
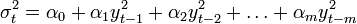
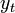 feltételes eloszlása ismét gaussi:
feltételes eloszlása ismét gaussi: 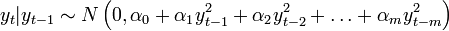
A legáltalánosabb GARCH(m,r) modell
Ha megvan a paraméterbecslés (pl: maximum likelihood-dal), akkor jóslást tehetünk a volatilitásra (csak 1 lépésre előre!):
Paraméterbecslés ARCH(1) modellre: maximum likelihood
az f() függvény az 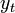 feltételes eloszlása:
feltételes eloszlása: 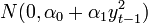
A –ln(L) minimuma fogja megadni az 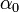 és
és 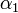 paramétereket.
paramétereket.