„Csega/Safety factor” változatai közötti eltérés
a |
|||
| 5. sor: | 5. sor: | ||
<math>\frac{\Delta \phi}{2 \pi}</math> | <math>\frac{\Delta \phi}{2 \pi}</math> | ||
| − | Tehát ha a mágneses erővonal a kezdőpozíciójába pontosan egy tórusz körüli körbefordulás után érkezik meg, akkor a <math>q | + | Tehát ha a mágneses erővonal a kezdőpozíciójába pontosan egy tórusz körüli körbefordulás után érkezik meg, akkor a <math>q = 1</math>. Ha ennél lassaban megy a poloidális irányban, nagyobb q értékkel fog rendelkezni. A racionális (m/n alakú) q értékek fontos szerepük van a stabilitásban. Ha a q = m/n alakú, ahol m és n egész számok, akkor az erővonal a tórusz körüli m toroidális és n poloidális körbefordulás után ér vissza önmagába. |
| + | |||
| + | [[Image:q_value.png|center|thumb|Erővonal a q=2 felületen (a tórusz felülnézeti képén)]] | ||
<references/> | <references/> | ||
A lap 2011. november 30., 12:06-kori változata
A biztonsági faktor [1] (safety factor - jele: q) a stabilitás meghatározásában játszik fontos szerepet. Általánosan elmondható, hogy a nagyobb q érték nagyobb stabilitást jelent. Ezen kívül fontos szerepet játszik a transport theoryban is.
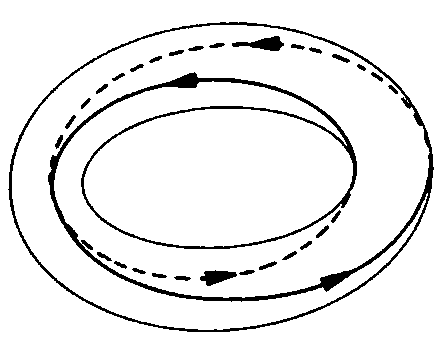
Axiszimmetrikus egyensúlyban minden erővonalnak megvan a saját q értéke. Az erővonalak a hozzájuk rendelt, tórusz alakú mágneses felületen futó, helikális pályát követnek. Ha egy adott toroidális szögnél (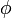 ) az erővonal a poloidális síkon egy adott pozícióban található, előbb-utóbb vissza fog térni a poloidális síknak ugyanabba a pozíciójába
) az erővonal a poloidális síkon egy adott pozícióban található, előbb-utóbb vissza fog térni a poloidális síknak ugyanabba a pozíciójába 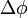 szögelfordulás után. Ezen erővonal q-értékét a következő képlet adja meg:
szögelfordulás után. Ezen erővonal q-értékét a következő képlet adja meg:
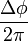
Tehát ha a mágneses erővonal a kezdőpozíciójába pontosan egy tórusz körüli körbefordulás után érkezik meg, akkor a 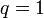 . Ha ennél lassaban megy a poloidális irányban, nagyobb q értékkel fog rendelkezni. A racionális (m/n alakú) q értékek fontos szerepük van a stabilitásban. Ha a q = m/n alakú, ahol m és n egész számok, akkor az erővonal a tórusz körüli m toroidális és n poloidális körbefordulás után ér vissza önmagába.
. Ha ennél lassaban megy a poloidális irányban, nagyobb q értékkel fog rendelkezni. A racionális (m/n alakú) q értékek fontos szerepük van a stabilitásban. Ha a q = m/n alakú, ahol m és n egész számok, akkor az erővonal a tórusz körüli m toroidális és n poloidális körbefordulás után ér vissza önmagába.
- ↑ Wesson: Tokamaks (3. kiadás, 111. old)