„Mintázat 4.óra” változatai közötti eltérés
(→Bevezető) |
(→Folyadékdinamikát leíró fontos paraméterek, fogalmak) |
||
| 40. sor: | 40. sor: | ||
<math>Ca=\frac{\rho \nu U}{\sigma}</math> (viszkozitás/görbület) | <math>Ca=\frac{\rho \nu U}{\sigma}</math> (viszkozitás/görbület) | ||
| + | |||
| + | |||
| + | <b>Konvektív</b> az az instabilitás, ahol a perturbáció egy áramlási vonal mentén előrehaladva erősödik fel, de a keletkezés helyén nem, <b>abszolút</b> instabilitás esetén az áramlás nem tudja elmosni a zajt, helyben erősödik fel, általában globálisan megfigyelhető. | ||
=== Perturbációszámítás dióhéjban === | === Perturbációszámítás dióhéjban === | ||
A lap 2011. december 19., 14:41-kori változata
Tartalomjegyzék
Bevezető
Használt jelölések:
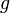 : gravitációs gyorsulás
: gravitációs gyorsulás
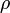 : sűrűség
: sűrűség
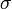 : felületi feszültség
: felületi feszültség
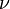 : kinematikai viszkozitás
: kinematikai viszkozitás
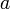 : tipikus méret
: tipikus méret
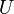 : sebesség
: sebesség
Folyadékdinamikát leíró fontos paraméterek, fogalmak
Reynold-szám (pl. lamináris-turbulens átmenet jellemzése áramlásoknál):
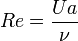 (inercia/viszkozitás)
(inercia/viszkozitás)
Froude-szám (a Mach-szám folyadékdinamikai megfelelője):
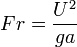 (inercia/gravitáció)
(inercia/gravitáció)
Eötvös- vagy Bond- szám (cseppek, kapillárisok leírása):
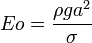 (gravitáció/görbület)
(gravitáció/görbület)
a kapilláris hossz:
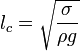
Weber szám (két folyadék határfelületén lezajló jelenségek jellemzésére):
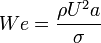 (inercia/görbület)
(inercia/görbület)
Kapilláris szám (porózus anyagba folyadékot préselünk):
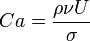 (viszkozitás/görbület)
(viszkozitás/görbület)
Konvektív az az instabilitás, ahol a perturbáció egy áramlási vonal mentén előrehaladva erősödik fel, de a keletkezés helyén nem, abszolút instabilitás esetén az áramlás nem tudja elmosni a zajt, helyben erősödik fel, általában globálisan megfigyelhető.