„Mintázat 3.óra” változatai közötti eltérés
(→Bevezetés) |
(→Wulff-szerkesztés) |
||
| 14. sor: | 14. sor: | ||
== Wulff-szerkesztés == | == Wulff-szerkesztés == | ||
| + | |||
| + | Ha van egy <math>r(\phi)</math> felületünk, akkor a Wulff-szerkesztés segítségével egy integrációs konstans erejéig meg tudjuk határozni a <math>\sigma(\theta)</math> felületi feszültség értékét. Ennek a menete a következő: | ||
| + | |||
| + | - Veszünk egy <math>r(\phi)</math> pontot és megszerkesztjük az érintőjét | ||
| + | |||
| + | - Erre az érintőre a az origóból merőlegest állítunk | ||
| + | |||
| + | - A két egyenes metszéspontja megadja <math>\sigma(\theta)</math> értékét ( <math>\theta</math> az érintőre állított merőleges x temgellyel bezárt szöge) | ||
| + | |||
| + | Ha a mintázatban van "egyenes" szakasz, akkor csúcsos lesz a felületi feszültség, ha nibcs, akkor nem lesz csúcsos. | ||
== Determinisztikus káosz == | == Determinisztikus káosz == | ||
== Nemlineáris viselkedés a kémiában == | == Nemlineáris viselkedés a kémiában == | ||
A lap 2011. december 20., 15:31-kori változata
Tartalomjegyzék
Bevezetés
Túlhűtött folyadékok megszilárdulásakor mintázatok képződnek, mivel nem egyensúlyi folyamatról van szó. A határvonalat általánosan leírhatjuk egy 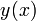 függvénnyel, de mivel a megszilárdulás általában egy nukleációs pontból indul ki, érdemes áttérni molárkoordinátás leírásra (
függvénnyel, de mivel a megszilárdulás általában egy nukleációs pontból indul ki, érdemes áttérni molárkoordinátás leírásra (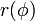 ).
). 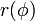 egyértelműen meghatározza
egyértelműen meghatározza 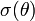 felületi feszültséget.
felületi feszültséget.
A felületi szabadenergiát a következőképp definiáljuk:
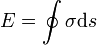
Az egyensúly feltétele:
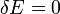 és
és
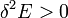 azaz
azaz 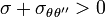
Wulff-szerkesztés
Ha van egy 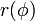 felületünk, akkor a Wulff-szerkesztés segítségével egy integrációs konstans erejéig meg tudjuk határozni a
felületünk, akkor a Wulff-szerkesztés segítségével egy integrációs konstans erejéig meg tudjuk határozni a 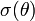 felületi feszültség értékét. Ennek a menete a következő:
felületi feszültség értékét. Ennek a menete a következő:
- Veszünk egy 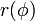 pontot és megszerkesztjük az érintőjét
pontot és megszerkesztjük az érintőjét
- Erre az érintőre a az origóból merőlegest állítunk
- A két egyenes metszéspontja megadja 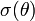 értékét (
értékét ( 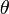 az érintőre állított merőleges x temgellyel bezárt szöge)
az érintőre állított merőleges x temgellyel bezárt szöge)
Ha a mintázatban van "egyenes" szakasz, akkor csúcsos lesz a felületi feszültség, ha nibcs, akkor nem lesz csúcsos.