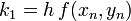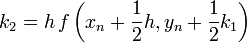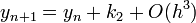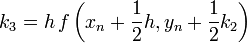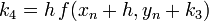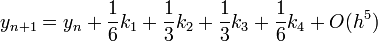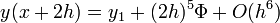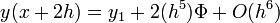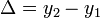„Numerikus módszerek” változatai közötti eltérés
(Új oldal, tartalma: „== Diffegyenlet-megoldó módszerek == ===Euler-módszer=== A legegyszerűbb egylépéses módszer. Az y(x=0)=y0 kezdőfeltétellel megadott, y’=f(x,y) diffegyenlet mego…”) |
|||
| 50. sor: | 50. sor: | ||
<math>h_0 = h_1 \left | \frac{\Delta_0}{\Delta_1} \right | ^{0.2}</math> | <math>h_0 = h_1 \left | \frac{\Delta_0}{\Delta_1} \right | ^{0.2}</math> | ||
| − | Ha <math>h_1>h_0</math>, akkor meg kell ismételni a | + | Ha <math>h_1>h_0</math>, akkor meg kell ismételni a számolást egy kisebb lépéssel, ha pedig <math>h_1<h_0</math>, akkor a következő lépésben használhatjuk <math>h_0</math>-t lépésként. |
A lap 2011. június 8., 15:45-kori változata
Tartalomjegyzék
Diffegyenlet-megoldó módszerek
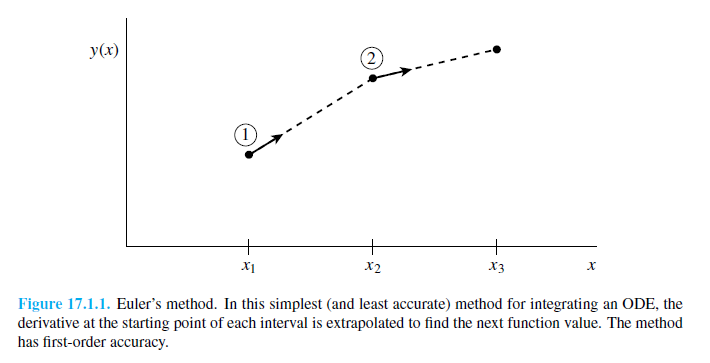
Euler-módszer
A legegyszerűbb egylépéses módszer. Az y(x=0)=y0 kezdőfeltétellel megadott, y’=f(x,y) diffegyenlet megoldása esetén az Euler lépés alakja (Taylor-sorfejtés első két tagja):
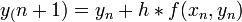
Hibája: Taylor-sorfejtést tovább írjuk, a különbség 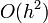 lesz. Használata nem javasolt, mert a hibák hamar felösszegződnek, a megoldás „felrobban”. Ennek elkerülésére érdemes lehet használni az implicit Euler-módszert:
lesz. Használata nem javasolt, mert a hibák hamar felösszegződnek, a megoldás „felrobban”. Ennek elkerülésére érdemes lehet használni az implicit Euler-módszert: 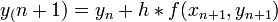 . Ez nagy h értékekre is stabil marad.
. Ez nagy h értékekre is stabil marad.
Runge-Kutta módszer
Miért használjuk? Mert sokkal pontosabb, mint az Euler-módszer.
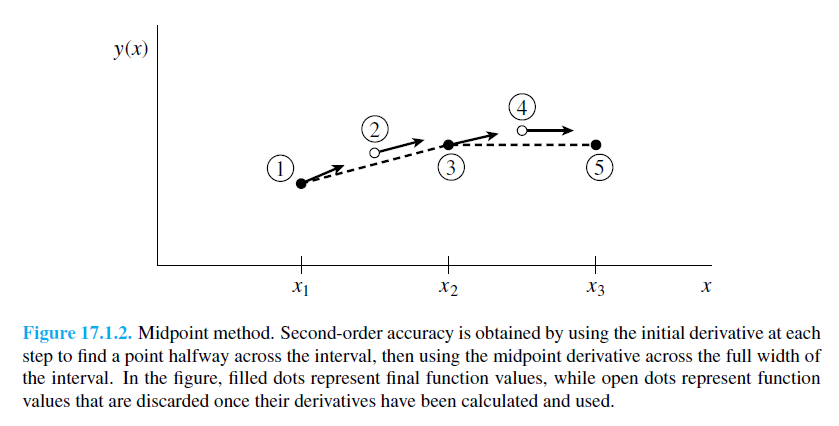
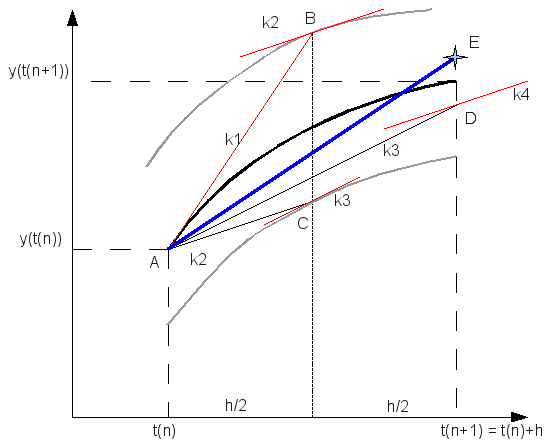
Másodrendű RK (vagy midpoint method - középponti módszer)
Ez a módszer tehát harmadrendig pontos. Általánosan az n-ed rendű RK-nak 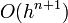 hibája van.
hibája van.
Negyedrendű RK
A negyedrendű módszerben négyszer kell kiértékelni az f függvényt, míg az Euler-módszernél egyszer kellett. Ezért ennek a használata akkor gazdaságos, ha ugyanakkora pontosság mellett legalább négyszer akkora lehet a lépésköz.
Adaptív RK
Egy differenciálegyenlet megoldása során lehetnek gyorsan és lassan változó szakaszok a függvényben. A lassan változó szakaszok integrálása során nagyobb lépéseket is tehetünk a hiba növekedése nélkül. Ennek a megoldására szolgál az adaptív Runge-Kutta módszer. Alapötlete, hogy egy lépést tegyünk meg egyszer teljesen (2h-val, 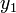 ), egyszer pedig két fél lépésben (h-val,
), egyszer pedig két fél lépésben (h-val, 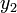 ). Mindegyik lépés 4 függvény kiértékelést igényel (3*4), de ebből kettő megegyezik, így 11 kiértékelés szükséges a 2*4 helyett, ami a két fél lépésből jönne össze.
). Mindegyik lépés 4 függvény kiértékelést igényel (3*4), de ebből kettő megegyezik, így 11 kiértékelés szükséges a 2*4 helyett, ami a két fél lépésből jönne össze.
A kettő közti különbség:
A különbség 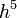 -nel skálázik. Ha egy
-nel skálázik. Ha egy 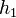 lépés eredménye
lépés eredménye 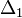 , és mi
, és mi 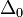 hibát akarunk elérni, akkor
hibát akarunk elérni, akkor 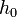 lépést kell tennünk, ami:
lépést kell tennünk, ami:
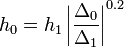
Ha 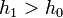 , akkor meg kell ismételni a számolást egy kisebb lépéssel, ha pedig
, akkor meg kell ismételni a számolást egy kisebb lépéssel, ha pedig 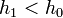 , akkor a következő lépésben használhatjuk
, akkor a következő lépésben használhatjuk 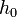 -t lépésként.
-t lépésként.