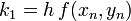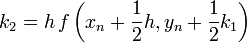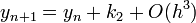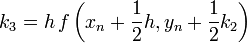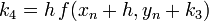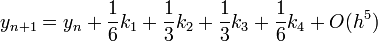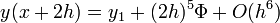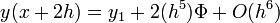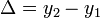„Numerikus módszerek” változatai közötti eltérés
| 59. sor: | 59. sor: | ||
===Szimulált hőkezelés=== | ===Szimulált hőkezelés=== | ||
| + | A módszer elnevezése az anyagtudomány területéről ered, ahol hőkezelési eljárásokkal lehet változtatni egy anyag kristályosodási méretét. Számítógépes módszerként egy sokdimenziód függvény energiaminimumának megkeresésére lehet használni. | ||
| + | |||
| + | Működési struktúra: | ||
| + | # Válasszunk egy tetszőleges kezdőállapotot (i) | ||
| + | # Válasszuk ki az egyik szomszédot (j) | ||
| + | # Ha a szomszéd energiája kisebb, átlépünk rá | ||
| + | # Ha nagyobb a szomszéd energiája, az energiakülönbség, és egy globális T paraméter által meghatározott valószínűség szerint elfogadjuk a nagyobb energiájú helyet | ||
| + | |||
| + | Az elfogadási valószínűségek tehát: | ||
| + | * ha f(j) ≤ f(i), akkor 1 | ||
| + | * ha f(j) > f(i), akkor <math>e^{\frac{f(i)-f(j)}{T}}</math> | ||
| + | |||
| + | A T hőmérsékletet kezdetben nagynak választva, majd folyamatosan csökkentve ezzel a módszerrel megtalálhatjuk a függvény globális minimumát. | ||
A lap 2011. június 9., 10:38-kori változata
Tartalomjegyzék
Diffegyenlet-megoldó módszerek
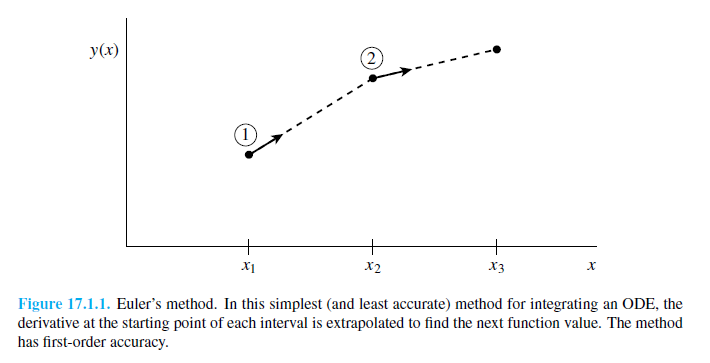
Euler-módszer
A legegyszerűbb egylépéses módszer. Az y(x=0)=y0 kezdőfeltétellel megadott, y’=f(x,y) diffegyenlet megoldása esetén az Euler lépés alakja (Taylor-sorfejtés első két tagja):
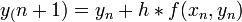
Hibája: Taylor-sorfejtést tovább írjuk, a különbség 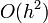 lesz. Használata nem javasolt, mert a hibák hamar felösszegződnek, a megoldás „felrobban”. Ennek elkerülésére érdemes lehet használni az implicit Euler-módszert:
lesz. Használata nem javasolt, mert a hibák hamar felösszegződnek, a megoldás „felrobban”. Ennek elkerülésére érdemes lehet használni az implicit Euler-módszert: 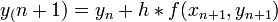 . Ez nagy h értékekre is stabil marad.
. Ez nagy h értékekre is stabil marad.
Runge-Kutta módszer
Miért használjuk? Mert sokkal pontosabb, mint az Euler-módszer.
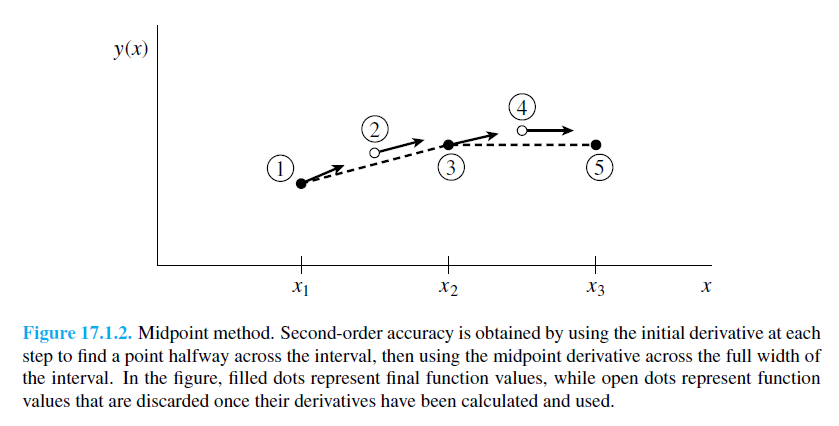
Másodrendű RK (vagy midpoint method - középponti módszer)
Ez a módszer tehát harmadrendig pontos. Általánosan az n-ed rendű RK-nak 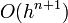 hibája van.
hibája van.
Negyedrendű RK
A negyedrendű módszerben négyszer kell kiértékelni az f függvényt, míg az Euler-módszernél egyszer kellett. Ezért ennek a használata akkor gazdaságos, ha ugyanakkora pontosság mellett legalább négyszer akkora lehet a lépésköz.
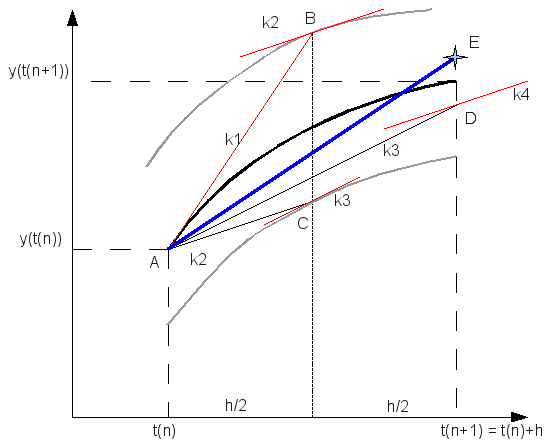
Adaptív RK
Egy differenciálegyenlet megoldása során lehetnek gyorsan és lassan változó szakaszok a függvényben. A lassan változó szakaszok integrálása során nagyobb lépéseket is tehetünk a hiba növekedése nélkül. Ennek a megoldására szolgál az adaptív Runge-Kutta módszer. Alapötlete, hogy egy lépést tegyünk meg egyszer teljesen (2h-val, 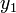 ), egyszer pedig két fél lépésben (h-val,
), egyszer pedig két fél lépésben (h-val, 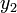 ). Mindegyik lépés 4 függvény kiértékelést igényel (3*4), de ebből kettő megegyezik, így 11 kiértékelés szükséges a 2*4 helyett, ami a két fél lépésből jönne össze.
). Mindegyik lépés 4 függvény kiértékelést igényel (3*4), de ebből kettő megegyezik, így 11 kiértékelés szükséges a 2*4 helyett, ami a két fél lépésből jönne össze.
A kettő közti különbség:
A különbség 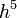 -nel skálázik. Ha egy
-nel skálázik. Ha egy 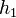 lépés eredménye
lépés eredménye 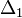 , és mi
, és mi 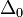 hibát akarunk elérni, akkor
hibát akarunk elérni, akkor 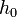 lépést kell tennünk, ami:
lépést kell tennünk, ami:
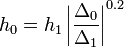
Ha 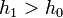 , akkor meg kell ismételni a számolást egy kisebb lépéssel, ha pedig
, akkor meg kell ismételni a számolást egy kisebb lépéssel, ha pedig 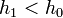 , akkor a következő lépésben használhatjuk
, akkor a következő lépésben használhatjuk 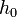 -t lépésként.
-t lépésként.
Egyenletrendszerek megoldása
Optimalizációs módszerek - szélsőérték keresés
Konjugált gradiens módszer
Szimulált hőkezelés
A módszer elnevezése az anyagtudomány területéről ered, ahol hőkezelési eljárásokkal lehet változtatni egy anyag kristályosodási méretét. Számítógépes módszerként egy sokdimenziód függvény energiaminimumának megkeresésére lehet használni.
Működési struktúra:
- Válasszunk egy tetszőleges kezdőállapotot (i)
- Válasszuk ki az egyik szomszédot (j)
- Ha a szomszéd energiája kisebb, átlépünk rá
- Ha nagyobb a szomszéd energiája, az energiakülönbség, és egy globális T paraméter által meghatározott valószínűség szerint elfogadjuk a nagyobb energiájú helyet
Az elfogadási valószínűségek tehát:
- ha f(j) ≤ f(i), akkor 1
- ha f(j) > f(i), akkor
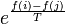
A T hőmérsékletet kezdetben nagynak választva, majd folyamatosan csökkentve ezzel a módszerrel megtalálhatjuk a függvény globális minimumát.