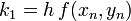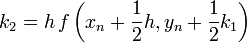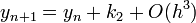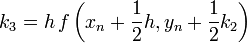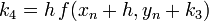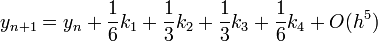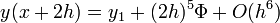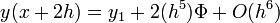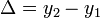„Numerikus módszerek” változatai közötti eltérés
| 53. sor: | 53. sor: | ||
==Egyenletrendszerek megoldása== | ==Egyenletrendszerek megoldása== | ||
| + | Lineáris egyenletrendszernek nevezzük az olyan egyenletrendszert, melyben minden változó az első hatványon szerepel. Ezeket felírhatjuk mátrixformában is: <math>A\vec{x} = \vec{b}</math>. Az ''A'' mátrixban tároljuk az egyenletrendszerben szereplő együtthatókat, <math>\vec{x}</math> vektor az ismeretlenek vektora, <math>\vec{b}</math> vektorban pedig az egyenletek jobb oldalainak értékei szerepelnek. Célunk meghatározni az <math>\vec{x}</math>-t, ehhez beszorozzuk jobbról az előző egyenletet ''A<sup>-1</sup>''-zel: <math>\vec{x} = A^{-1}\vec{b}</math>. A feladatunk tehát az ''A'' mátrix inverzét meghatározni. | ||
===Gauss-Jordan elimináció=== | ===Gauss-Jordan elimináció=== | ||
| + | A Gauss-elimináció során az ''A'' mátrix és a <math>\vec{b}</math> soraival '''egyszerre''' végzünk transzformációkat (másképp fogalmazva: az egyenleteket alakítjuk át). A megengedett transzformációk: | ||
| + | * mátrix két sorának felcserélése (két egyenlet cseréje) | ||
| + | * mátrix sorának számmal való szorzása | ||
| + | * a mátrix egy sorához egy másik skalárszorosának hozzáadása | ||
| + | A cél, hogy ilyen transzformációk sorozatának alkalmazásával ''A'' mátrixból egy felső háromszög mátrixok csináljunk. Ezután alulról fölfelé haladva behelyettesítéssel megkapjuk sorban <math>\vec{x}</math> elemeit. [http://hu.wikipedia.org/wiki/Gauss-elimin%C3%A1ci%C3%B3#P.C3.A9lda Példa] | ||
===LU dekompozíció=== | ===LU dekompozíció=== | ||
A lap 2011. június 9., 15:56-kori változata
Tartalomjegyzék
Diffegyenlet-megoldó módszerek
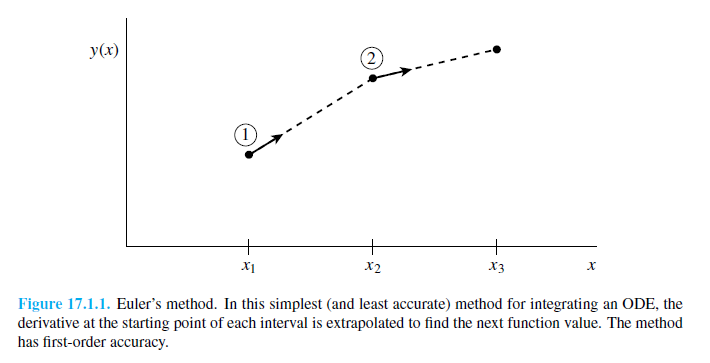
Euler-módszer
A legegyszerűbb egylépéses módszer. Az y(x=0)=y0 kezdőfeltétellel megadott, y’=f(x,y) diffegyenlet megoldása esetén az Euler lépés alakja (Taylor-sorfejtés első két tagja):
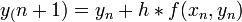
Hibája: Taylor-sorfejtést tovább írjuk, a különbség 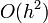 lesz. Használata nem javasolt, mert a hibák hamar felösszegződnek, a megoldás „felrobban”. Ennek elkerülésére érdemes lehet használni az implicit Euler-módszert:
lesz. Használata nem javasolt, mert a hibák hamar felösszegződnek, a megoldás „felrobban”. Ennek elkerülésére érdemes lehet használni az implicit Euler-módszert: 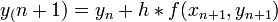 . Ez nagy h értékekre is stabil marad.
. Ez nagy h értékekre is stabil marad.
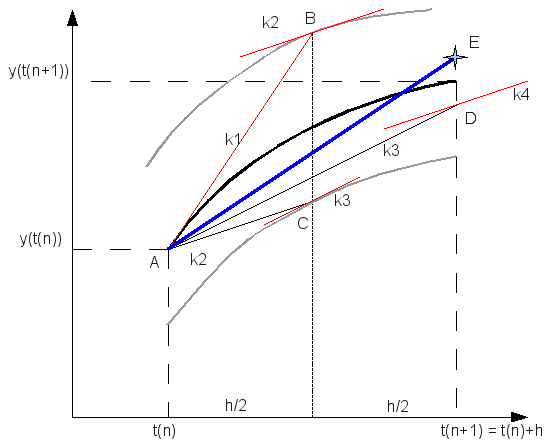
Runge-Kutta módszer
Miért használjuk? Mert sokkal pontosabb, mint az Euler-módszer.
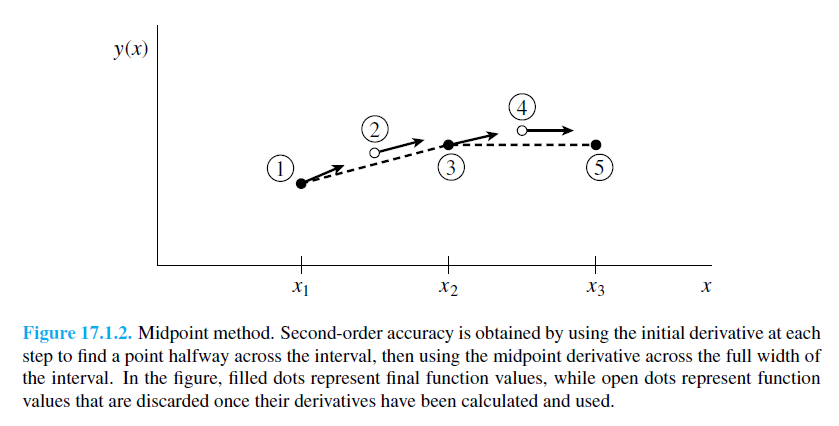
Másodrendű RK (vagy midpoint method - középponti módszer)
Ez a módszer tehát harmadrendig pontos. Általánosan az n-ed rendű RK-nak 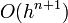 hibája van.
hibája van.
Negyedrendű RK
A negyedrendű módszerben négyszer kell kiértékelni az f függvényt, míg az Euler-módszernél egyszer kellett. Ezért ennek a használata akkor gazdaságos, ha ugyanakkora pontosság mellett legalább négyszer akkora lehet a lépésköz.
Adaptív RK
Egy differenciálegyenlet megoldása során lehetnek gyorsan és lassan változó szakaszok a függvényben. A lassan változó szakaszok integrálása során nagyobb lépéseket is tehetünk a hiba növekedése nélkül. Ennek a megoldására szolgál az adaptív Runge-Kutta módszer. Alapötlete, hogy egy lépést tegyünk meg egyszer teljesen (2h-val, 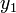 ), egyszer pedig két fél lépésben (h-val,
), egyszer pedig két fél lépésben (h-val, 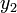 ). Mindegyik lépés 4 függvény kiértékelést igényel (3*4), de ebből kettő megegyezik, így 11 kiértékelés szükséges a 2*4 helyett, ami a két fél lépésből jönne össze.
). Mindegyik lépés 4 függvény kiértékelést igényel (3*4), de ebből kettő megegyezik, így 11 kiértékelés szükséges a 2*4 helyett, ami a két fél lépésből jönne össze.
A kettő közti különbség:
A különbség 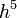 -nel skálázik. Ha egy
-nel skálázik. Ha egy 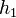 lépés eredménye
lépés eredménye 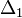 , és mi
, és mi 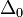 hibát akarunk elérni, akkor
hibát akarunk elérni, akkor 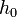 lépést kell tennünk, ami:
lépést kell tennünk, ami:
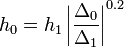
Ha 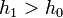 , akkor meg kell ismételni a számolást egy kisebb lépéssel, ha pedig
, akkor meg kell ismételni a számolást egy kisebb lépéssel, ha pedig 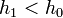 , akkor a következő lépésben használhatjuk
, akkor a következő lépésben használhatjuk 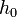 -t lépésként.
-t lépésként.
Egyenletrendszerek megoldása
Lineáris egyenletrendszernek nevezzük az olyan egyenletrendszert, melyben minden változó az első hatványon szerepel. Ezeket felírhatjuk mátrixformában is: 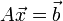 . Az A mátrixban tároljuk az egyenletrendszerben szereplő együtthatókat,
. Az A mátrixban tároljuk az egyenletrendszerben szereplő együtthatókat, 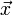 vektor az ismeretlenek vektora,
vektor az ismeretlenek vektora, 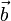 vektorban pedig az egyenletek jobb oldalainak értékei szerepelnek. Célunk meghatározni az
vektorban pedig az egyenletek jobb oldalainak értékei szerepelnek. Célunk meghatározni az 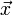 -t, ehhez beszorozzuk jobbról az előző egyenletet A-1-zel:
-t, ehhez beszorozzuk jobbról az előző egyenletet A-1-zel: 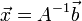 . A feladatunk tehát az A mátrix inverzét meghatározni.
. A feladatunk tehát az A mátrix inverzét meghatározni.
Gauss-Jordan elimináció
A Gauss-elimináció során az A mátrix és a 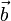 soraival egyszerre végzünk transzformációkat (másképp fogalmazva: az egyenleteket alakítjuk át). A megengedett transzformációk:
soraival egyszerre végzünk transzformációkat (másképp fogalmazva: az egyenleteket alakítjuk át). A megengedett transzformációk:
- mátrix két sorának felcserélése (két egyenlet cseréje)
- mátrix sorának számmal való szorzása
- a mátrix egy sorához egy másik skalárszorosának hozzáadása
A cél, hogy ilyen transzformációk sorozatának alkalmazásával A mátrixból egy felső háromszög mátrixok csináljunk. Ezután alulról fölfelé haladva behelyettesítéssel megkapjuk sorban 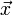 elemeit. Példa
elemeit. Példa
LU dekompozíció
Legyen A egy kvadratikus mátrix, erre az LU felbontás: A = LU. Az L és U mátrixok alsó illetve felső háromszög mátrixok (főátlóban is vannak elemek). Példa
Alkalmazása
- Determináns számolás: det(A) = det(L)*det(U)
- A háromszög mátrixok determinánsa a főátlóban lévő elemek szorzata, ezért ez nagyon egyszerűen számolható
- Mátrix inverz:
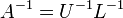
- Háromszög mátrix inverze könnyen számolható, ezért jó ez a felbontás.
Singular Value Decomposition - Szinguláris érték dekompozíció
Sokszor előfordul, hogy a mátrix, amit invertálni akarunk, közel van a szingulárishoz (det A ≈ 0), és sem a Gauss-elimináció, se az LU felbontás nem jár sikerrel.
Adott egy A mátrixunk, ami MxN méretű. Ezt a mátrixot felírhatjuk UWVT formában, ahol:
- U: MxN, oszlop-ortogonális mátrix
- W: NxN, diagonális, a szinguláris értékeket tartalmazza
- VT: NxN, ortogonális mátrix
A módszer segítségével nem-négyzetes mátrixokat is tudunk invertálni (pszeudoinverz) a következő módon:
![A^{-1} = V\,[diag(1/w_j)]\,U^T](/images/math/b/e/2/be29f4083659602a3acf54303900924a.png)
Ami problémát okozhat, az a szinguláris értékek reciproka, ha az nulla, vagy nagyon közel van nullához. A megoldás, hogy ebben az esetben az 1/wj-t nullának vesszük.
Optimalizációs módszerek - szélsőérték keresés
Konjugált gradiens módszer
Szimulált hőkezelés
A módszer elnevezése az anyagtudomány területéről ered, ahol hőkezelési eljárásokkal lehet változtatni egy anyag kristályosodási méretét. Számítógépes módszerként egy sokdimenziós függvény energiaminimumának megkeresésére lehet használni.
Működési struktúra:
- Válasszunk egy tetszőleges kezdőállapotot (i)
- Válasszuk ki az egyik szomszédot (j)
- Ha a szomszéd energiája kisebb, átlépünk rá
- Ha nagyobb a szomszéd energiája, az energiakülönbség, és egy globális T paraméter által meghatározott valószínűség szerint elfogadjuk a nagyobb energiájú helyet
Az elfogadási valószínűségek tehát:
- ha f(j) ≤ f(i), akkor 1
- ha f(j) > f(i), akkor
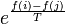
A T hőmérsékletet kezdetben nagynak választva, majd folyamatosan csökkentve ezzel a módszerrel megtalálhatjuk a függvény globális minimumát.