Relativitáselmélet

Matematikai alapok és fogalmak

A relativitáselmélet matematikai alapjai

Relativisztikus kinematika és dinamika

Relativisztikus kinematika és dinamika

Relativisztikus kvantummechanika

(ez egy külön oldal lenne, de nem sikerült egyből rájönnöm, hogy hogy kell új oldalt csinálni)

Ebben a részben 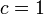$c = 1$

A Klein-Gordon egyenlet

Legyen 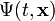$\Psi (t,\mathbf{x})$ egy részecske hullámfüggvénye, mint egy inerciarendszerbeli tér- és időkoordináták skalárfüggvénye. Erre szeretnénk felírni egy kovariáns egyenletet, ami összhangban van a relativitáselmélettel. Ehhez induljunk ki a 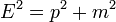$E^2 = p^2 + m^2$ egyenletből, és helyettesítsük a fizikai mennyiségeket a klasszikus kvantummechanikából ismert operátoraikkal. Az impulzus operátora: 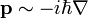$\mathbf{p} \sim -i \hbar \nabla$, az energiát az időderiváltnak feleltethetjük meg: 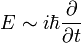$E \sim i \hbar \frac{\partial}{\partial t}$, a tömeg pedig itt is egy állandó. Így a fenti egyenletnek megfelelő operátorokat a hullámfüggvényre hattatva a következő egyenletet kapjuk:

$\left ( -\hbar^2 \frac{\partial^2}{\partial t^2} + \hbar^2 \nabla^2 - m^2 \right ) \Psi = 0$

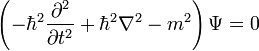
Ez a Klein-Gordon egyenlet. Ezt felírhatjuk négyesvektoros alakban is. Az energia és impulzus közötti összefüggés (diszperziós reláció) négyesvektorosan: 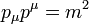$p_{\mu} p^{\mu} = m^2$. Az előző megfeleltetés operátoroknak ekkor: 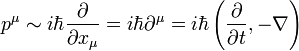$p^{\mu} \sim i \hbar \frac{\partial}{\partial x_{\mu}} = i \hbar \partial^{\mu} = i \hbar \left ( \frac{\partial}{\partial t}, -\nabla \right )$. A Klein-Gordon egyenlet ilyen alakban:

$\left ( \partial_{\mu} \partial^{\mu} + \frac{m^2}{\hbar^2} \right ) \Psi = 0$

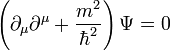
A Klein-Gordon egyenlet síkhullám megoldásait egyszerűen felírhatjuk:

$\Psi (x^{\mu}) = A e^{- i k_{\mu} x^{\mu} } = A e^{-i \omega t + i \mathbf{k x}}$

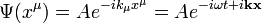
Ezt az egyenletbe behelyettesítve láthatjuk, hogy kielégíti azt, ha teljesül a 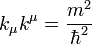$k_{\mu} k^{\mu} = \frac{m^2}{\hbar^2}$ feltétel. Ez azt jelenti, hogy a 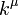$k^{\mu}$ négyesvektor komponenseiből csak 3 független. Legyyenek a komponensek: 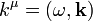$k^{\mu} = \left ( \omega, \mathbf{k} \right )$, így ezekre a 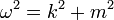$\omega^2 = k^2 + m^2$ diszperziós reláció adódik. A kvantummechanikában szokásos értelmezés szerint az energia (ez az időderiválás operátor sajátértéke is) 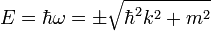$E = \hbar \omega = \pm \sqrt{\hbar^2 k^2 + m^2}$. Formálisan a pozitív energiás megoldás mellett van egy negatív energiájú is (ez jelenti majd az antirészecskéket).