Mintázat 6.óra

Az óra címe: határfelületi instabilitások megszilárdulás során. Ezen az órán a fontosabb geometriai elrendezésekről, valamint a különböző, ezen instabilitásokat leíró modellek vizsgálatával foglalkoztunk.

Fontosabb geometriai elrendezések

Az alábbi esetekben egy fontos egyszerűsítést tettünk: vékony mintával dolgozunk (ahol a konvekciót elhanyagolhatjuk, mert a vékony mintában a fázisátalakulás során felszabaduló látens hő hatására sem indul be áramlás).

• Szabad növekedés alatt azt értjük, amikor a fázisátalakulás kondenzációs magokból indul ki és az új fázis kialakulását, tovaterjedését nem korlátozza semmi. Szabad növekedés például túlhűtött folyadékban a szilárd fázis kialakulása.
• Irányított megszilárdulásról akkor beszélünk, ha a fázisátalakulás egy front mentén megy végbe. Ez általában úgy történik, hogy a rendszerünk egyik végét melegebb, a másikat pedig hidegebb állandó hőmérsékleten tartjuk, majd a mintát állandó v sebességel a melegebb oldaltól a hidegebb felé mozgatjuk.

TÁBLÁZAT A FONTOSABB PARAMÉTEREKRŐL!!!

A megszilárdulási folyamatokat leíró éleshatár modell

A túlhűtött folyadékban (vagy túltelített oldatban) növekedő kristály dinamikáját szeretnénk leírni (az egyszerűség kedvéért két dimenzióban). Az első mennyiség, amit nyomon kell követnünk, az egy skalártér, jelen esetben a hőmérséklet T(x,y,t), vagy (a túltelített oldat esetében) a kémiai koncentráció c(x,y,t). A továbbiakban a túlhűtött folyadékkal foglalkozunk, a leírás azonban nagyon hasonló túltelített oldat esetén is.

Az egységnyi hosszon átmenő hőáram: 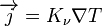$\overrightarrow{j} = K_{\nu} \nabla T$, ahol 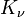$K_{\nu}$ a hővezetési tényező a 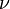$\nu$ = szilárd, folyadék oldalon.

Az energiamegmaradás: 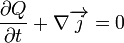$\frac{\partial Q}{\partial t} + \nabla \overrightarrow{j} = 0$, ahol 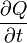$\frac{\partial Q}{\partial t}$ az egységnyi felületelem által időegységenként felvett (vagy leadott) hőt jelenti.

A hőáram képletét behelyettesítve az energiamegmaradás egyenletébe és fölhasználva, hogy 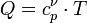$Q = c_p^{\nu} \cdot T$, megkapjuk a diffúziós egyenletet:

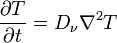$\frac{\partial T}{\partial t} = D_{\nu} \nabla^2 T$, mely a határfelület mindkét oldalán (szilárd és folyadék fázisban is) érvényes. A diffúziós állandó: 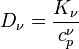$D_{\nu} = \frac{K_{\nu}}{c_p^{\nu}}$, ahol 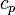$c_p$ az egységnyi felületre vonatkozó fajhő.

A megszilárdulás során L látens hő keletkezik. A határfelület normális sebességét 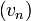$\left( v_n \right)$ az energiamegmaradásból számolhatjuk:

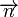$L \cdot \overrightarrow{v_n} = \left[ D^{solid}c_p^{solid} \left( \nabla T\right)^{solid} - D^{liquid}c_p^{liquid} \left( \nabla T \right)^{liquid} \right] \cdot \overrightarrow{n}$, ahol $\overrightarrow{n}$ a határfelület adott pontjának normálvektora.

Különböző (éleshatár, fázismező, DLA) modellek

Polikristályok

<<<Vissza az óra nyitólapjára