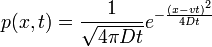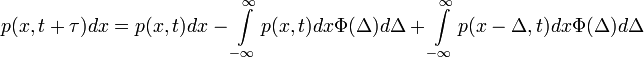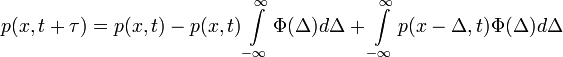VélFiz 1.tétel
Tartalomjegyzék
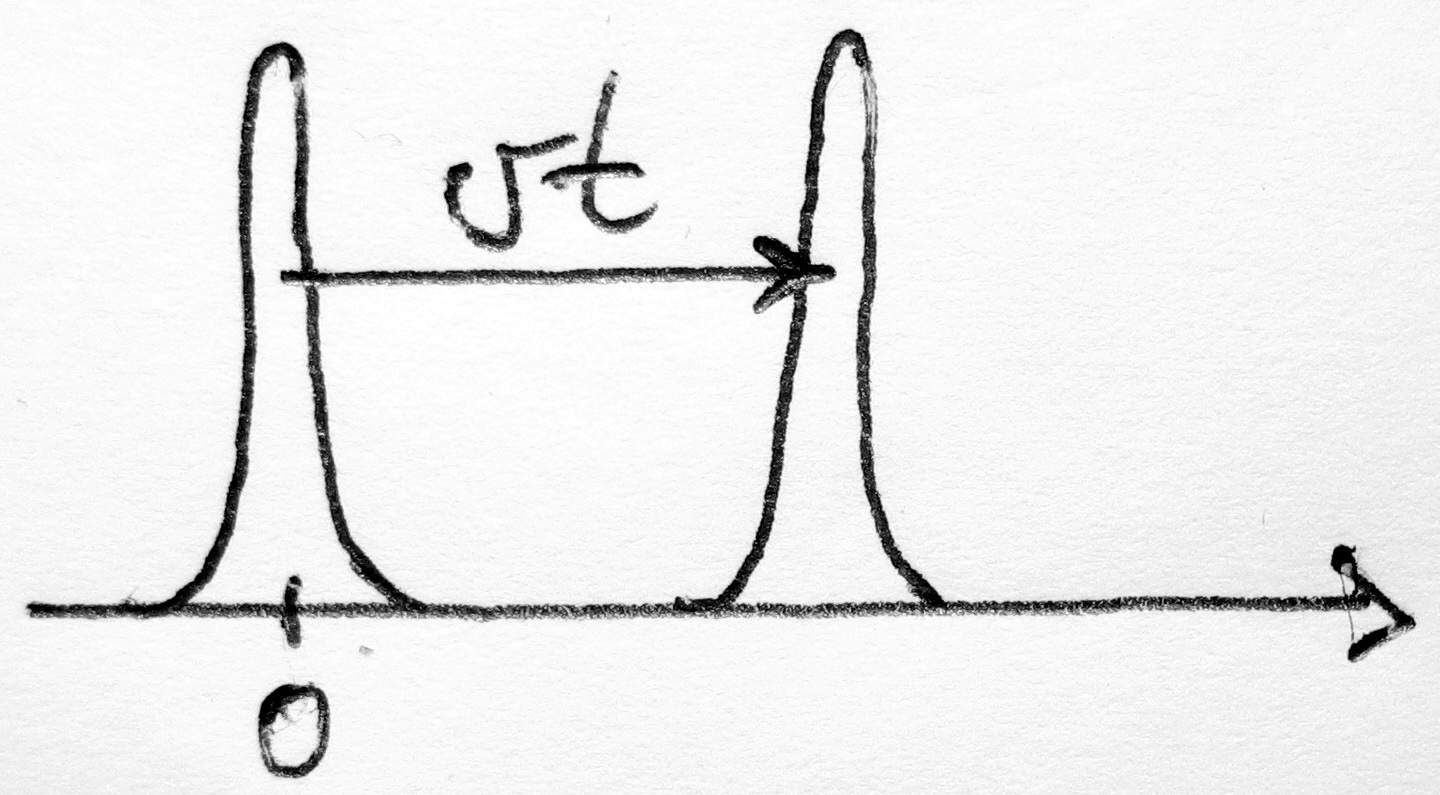
1. tétel: Brown-mozgás: Einstein levezetése
Alapfeltevések
- A részecskék egymástól függetlenül mozognak.
-
 << megfigyelési idő minimuma (ezen túl a mozgás az előzőektől függetlennek tekinthető)
<< megfigyelési idő minimuma (ezen túl a mozgás az előzőektől függetlennek tekinthető) - Az elmozdulásnak van egy valószínűségi eloszlása. A mozgás leírható valószínűségi alapon.
Jelölések
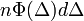 : annak valószínűségét adja meg, hogy n darab részecske
: annak valószínűségét adja meg, hogy n darab részecske 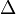 -t ugrik
-t ugrik  idő alatt.
idő alatt.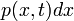 : annak valószínűsége, hogy t időpontban alatt x-ben van a részecske.
: annak valószínűsége, hogy t időpontban alatt x-ben van a részecske.
Einstein-féle leírás (1905)
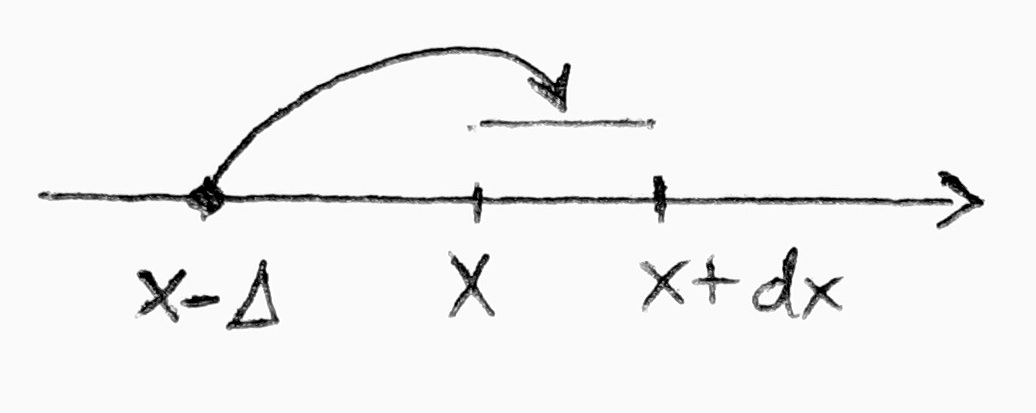
Annak valószínűsége, hogy a részecske  idő múlva az x és x+dx közötti tartományban foglal helyet:
idő múlva az x és x+dx közötti tartományban foglal helyet:
- Az egyenlet jobb oldalának első tagja annak valószínűsége, hogy a részecske már t időpillanatban is az x és x+dx közötti tartományban volt. A második tag annak valószínűségét adja meg, hogy
 idő múlva éppen arrébbmegy egy bármekkora
idő múlva éppen arrébbmegy egy bármekkora 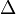 ugrással másik helyre. A harmadik tag annak valószínűségét adja, hogy a részecske valamekkora
ugrással másik helyre. A harmadik tag annak valószínűségét adja, hogy a részecske valamekkora 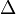 távolságról éppen
távolságról éppen 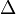 -t ugorva megérkezik
-t ugorva megérkezik  idő múlva.
idő múlva.
- Az egyenletet dx-szel végigoszthatjuk hiszen a dx-ek (és a p(x,t) is) mindegyik integráljel elé kiemelhetőek, hiszen nem függnek
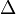 -tól, ekkor:
-tól, ekkor:
- És mivel
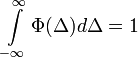 (hiszen
(hiszen 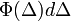 annak valószínűségét adja meg, hogy egy részecske
annak valószínűségét adja meg, hogy egy részecske 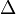 -t ugrik
-t ugrik  idő alatt, aminek a valószínűsége a teljes térre egy kell, hogy legyen - itt jegyzem meg, hogy
idő alatt, aminek a valószínűsége a teljes térre egy kell, hogy legyen - itt jegyzem meg, hogy 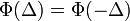 ), ennek következtében a bal oldal első két tagja kiejti egymást és az egyenlet a következő alakra egyszerűsödik:
), ennek következtében a bal oldal első két tagja kiejti egymást és az egyenlet a következő alakra egyszerűsödik:
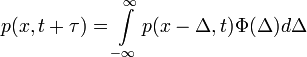
Chapman-Kolmogorov egyenlet
A fenti egyenletet  -ban és
-ban és 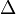 -ban sorbafejtjük, az alábbiak szerint:
-ban sorbafejtjük, az alábbiak szerint:
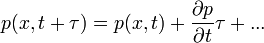
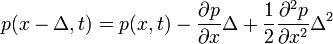
Ekkor a következő egyenletet kapjuk:
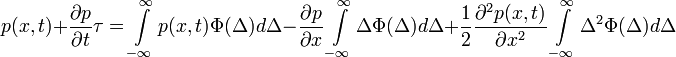
Ugyanazon okok miatt, mint a Chapman-Kolmogorov egyenlet levezetésénél, az egyenlet bal oldalának első tagja és jobb oldalának első tagja kiejti egymást, így a következő marad:
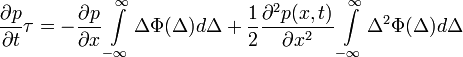
A fenti egyenlet jobb oldalán az első tagnál az integrál pont 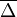 értékét adja meg, míg a második tag integrálját ennek mintájára elneveztük
értékét adja meg, míg a második tag integrálját ennek mintájára elneveztük 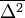 -nek. Az egyenlet a következőképp módosul:
-nek. Az egyenlet a következőképp módosul:
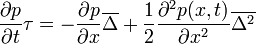
Ám 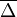 értéke nulla, mivel a
értéke nulla, mivel a 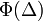 függvényt teljesen szimmetrikusnak tételeztük fel. Tehát a bal oldal első tagja is kiesik. Ami marad:
függvényt teljesen szimmetrikusnak tételeztük fel. Tehát a bal oldal első tagja is kiesik. Ami marad:
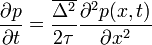
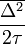 -et D-nek (azaz diffúziós együtthatónak) elnevezve megkapjuk a diffúziós egyenlet általános alakját, mely:
-et D-nek (azaz diffúziós együtthatónak) elnevezve megkapjuk a diffúziós egyenlet általános alakját, mely:
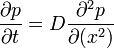
Dinamikai egyenlet a valószínűség időbeni változására (más néven a Fokker-Planck egyenlet).
Becslés a diffúziós együttható értékére
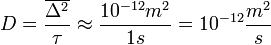
A Fokker-Planck egyenlet megoldásának keresése
A következőkben a Fokker-Planck egyenlet megoldását kerestük a t = 0, x = 0 kezdőfeltételekhez.
Ekkor ha 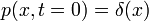 akkor ebből a megoldás:
akkor ebből a megoldás:
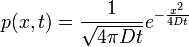 (3D-ben az 1/gyök-ös rész a 3/2-en van.)
(3D-ben az 1/gyök-ös rész a 3/2-en van.)
A fentiek alapján 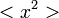 értékére az alábbi összefüggés születik, ahol
értékére az alábbi összefüggés születik, ahol 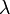 -t konstansnak várjuk:
-t konstansnak várjuk:
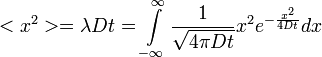 =
=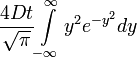
az utolsó egyelőségnél változó helyettesítés történt: 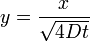
Az integrál értéke innen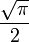 így:
így:
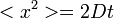 (azaz
(azaz 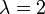 )
)
Sodródás
A részecskék ebben az esetben valamilyen kitüntetett irányba sodródnak: 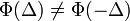
Az előzőekhez képest annyi a különbség, hogy a következő tag:
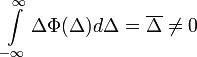
Ismét alkalmazva a Kramers-Moyal sorfejtést:
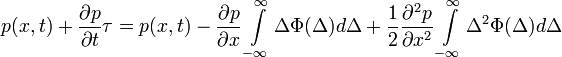
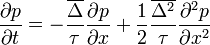
(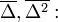 mikroszkopikus hossz,
mikroszkopikus hossz, 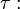 mikroszkopikus idő.)
mikroszkopikus idő.)
Ez is a Fokker-Planck egyenlet egy alakja. A fenti egyenlet jobb oldalán az első tag önmagában egy driftet ír le:
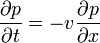 , ahol
, ahol 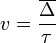
Például: 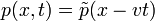 . A fenti egyenletbe behelyettesítve és elvégezve:
. A fenti egyenletbe behelyettesítve és elvégezve: 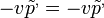
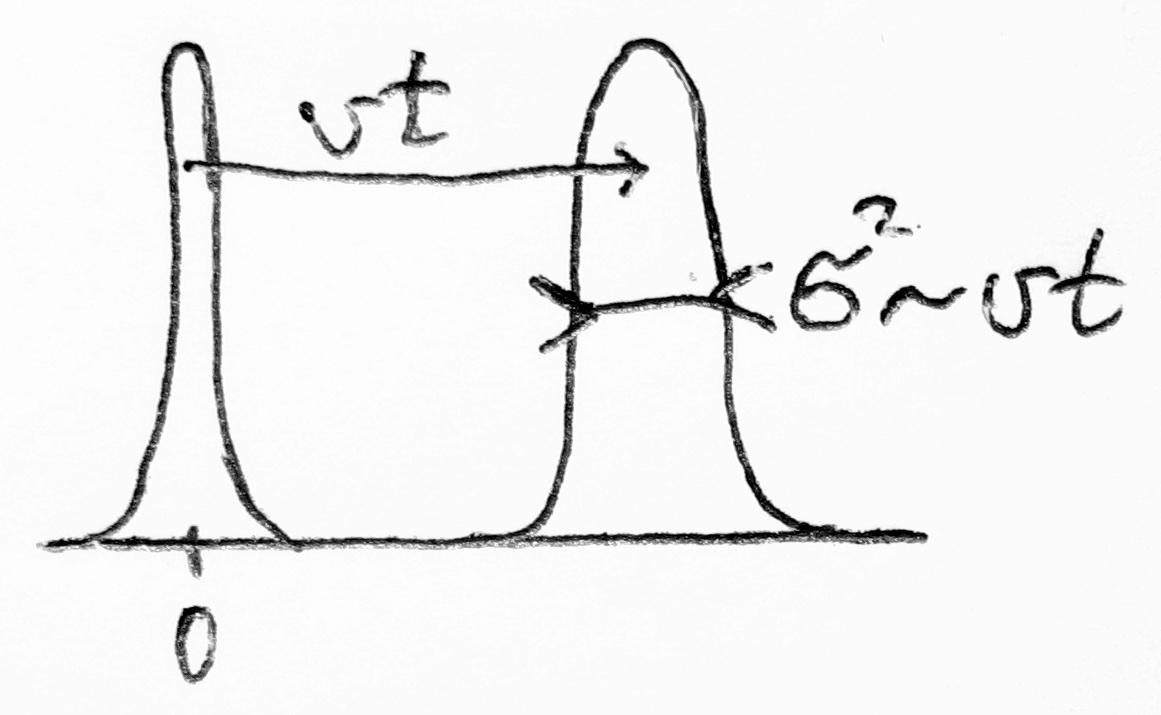
Viszont érdemes megtartani a második tagot, hiszen ha ezt is figyelembe vesszük, akkor azt kapjuk, hogy a "csomag" halad valamerre és közben szétterjed:
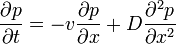
Bevezetve a 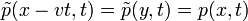 átalakítást az egyenlet a következőképpen módosul:
átalakítást az egyenlet a következőképpen módosul:
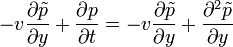 Innen:
Innen:
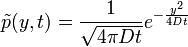 -->
-->