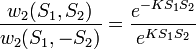VélFiz 4.tétel
Tartalomjegyzék
4. tétel: Egyensúlyhoz relaxálás, feltételek az átmeneti valószínűségekre
megjegyzés: a jobb olvashatóság érdekében: n'=m; n''=h
- Tegyük fel, hogy meg tudom úgy adni az átmeneti valószínűségeket, hogy a rendszer beugorjon az egyensúlyi állapotba.
- Hogyan kell megválasztani az átmeneti valószínűségeket?
Az átmeneti valószínűségek megválasztása
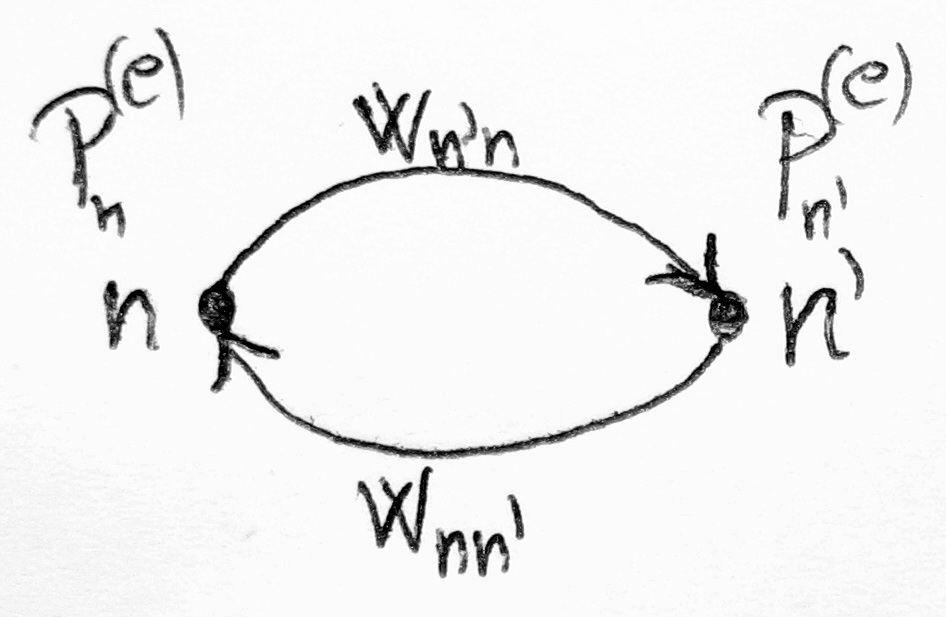
- Egyensúlyban időtükrözési szimmetria van.
Számolom, hogy (irány szerint megkülönböztetve) hányszor megy egyikből a másik állapotba a rendszer.
- Stacionárius állapotban
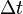 idő alatt az átmenetek száma:
idő alatt az átmenetek száma:
- n-ből m-be menve:
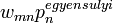
- m-ből n-be menve:
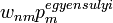
- n-ből m-be menve:
- A részletes egyensúly elve azt mondja ki, hogy a két számnak meg kell egyeznie, azaz:
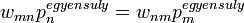
Megkötés az átmeneti valószínűségek hányadosára
Ha az állapotok száma véges és a rendszer minden pontjából minden másik pontjába el tudok jutni, akkor egyetlen stacionárius állapot lesz, az egyensúlyi.
Csak az átmeneti valószínűségek hányadosára van megkötés, azaz:
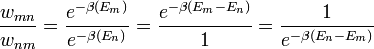
Ha 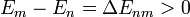 (azaz az energia nő), az e-ados tag 1-nél kisebb lesz, tehát vehetem azt az átmeneti valószínűségnek. Ha csökken az energia, akkor az energiacsökkenés felé vivő lépést 1 valószínűséggel lépem meg.
(azaz az energia nő), az e-ados tag 1-nél kisebb lesz, tehát vehetem azt az átmeneti valószínűségnek. Ha csökken az energia, akkor az energiacsökkenés felé vivő lépést 1 valószínűséggel lépem meg.
Bizonyítás: 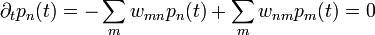 (egyensúly esetén). Tehát:
(egyensúly esetén). Tehát:
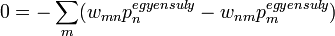 Páronként kioltják egymást. Ezért hívják részletes egyensúlynak, mivel nem csak az egész összeg nulla, hanem az állapotok között páronként van egyensúly. (Ehhez egy összefüggő gráf kell)
Páronként kioltják egymást. Ezért hívják részletes egyensúlynak, mivel nem csak az egész összeg nulla, hanem az állapotok között páronként van egyensúly. (Ehhez egy összefüggő gráf kell)
A dinamikai mátrix felírása
Egy N-állapotú rendszer adott állapotainak valószínűségeit - időtől függően - felírhatjuk vektoros alakban, a következőképpen:
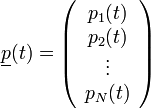
Ekkor a Master egyenlet a következőképp néz ki:
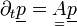
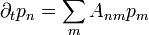
, ahol 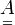 a rendszer dinamikai mátrixa, kiszámítása pedig a következőképpen történik:
a rendszer dinamikai mátrixa, kiszámítása pedig a következőképpen történik:
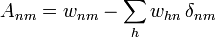
A rendszer dinamikai mátrixának kiszámítási módja
A mátrix elemeit összeadva a következőket kapjuk:
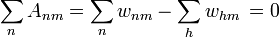 Az egységmátrixot hozzáadva A mátrixhoz sztochasztikus mátrixot kapunk. A kivonásnál a két szummás tag egyenlő adott értéknél, csak az összegzési index más.
Az egységmátrixot hozzáadva A mátrixhoz sztochasztikus mátrixot kapunk. A kivonásnál a két szummás tag egyenlő adott értéknél, csak az összegzési index más.
Perron-Frobenius elv [1]
A fenti mátrix 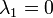 sajátértéke a legnagyobb, nem degenerált sajátállapothoz tartozik. Ez tulajdonképpen azt jelenti, hogy létezik egy (és csak egy) olyan megoldás, amire a sajátérték nulla. A legkisebb sajátérték sem degenerált.
sajátértéke a legnagyobb, nem degenerált sajátállapothoz tartozik. Ez tulajdonképpen azt jelenti, hogy létezik egy (és csak egy) olyan megoldás, amire a sajátérték nulla. A legkisebb sajátérték sem degenerált.
A 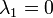 -hoz a
-hoz a 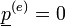 megoldás tartozik.
megoldás tartozik.
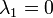 -> minden komponense pozitív:
-> minden komponense pozitív: 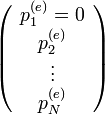 ;
; 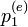 állapot egyensúlyban kiürülne, ezért ez nem jó. Továbbá a valószínűség szórzódás miatt se lehet 0, különben sorra az összesnek 0-nak kéne lennie.
állapot egyensúlyban kiürülne, ezért ez nem jó. Továbbá a valószínűség szórzódás miatt se lehet 0, különben sorra az összesnek 0-nak kéne lennie.
Ha a többi 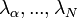 sajátértékhez nézzük az időfejlődést, pl.:
sajátértékhez nézzük az időfejlődést, pl.: 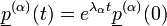 . Látható, hogy ebben az esetben a rendszer divergál. Azonban ha a sajátértékek mindegyike
. Látható, hogy ebben az esetben a rendszer divergál. Azonban ha a sajátértékek mindegyike 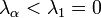 , akkor a rendszer az egyensúlyi állapothoz fog konvergálni az időfejlődése során.
, akkor a rendszer az egyensúlyi állapothoz fog konvergálni az időfejlődése során.
Tegyük fel, hogy mégis degenerált a 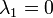 sajátérték, ekkor van másik egyensúlyi állapot (ahol nincs 0 elem):
sajátérték, ekkor van másik egyensúlyi állapot (ahol nincs 0 elem):
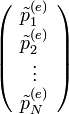
De ha van két ilyen állapot, akkor azok lineárkombinációja is egyensúlyi állapot (mivel a Master-egyenlet lineáris):
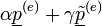 .
.
Ám ekkor elérhető - alfa és gamma értékek változtatásával -, hogy az egyik komponens nulla legyen. Ekkor viszont ellenmondásra jutottunk a korábbi állításunkkal, miszerint a sajátvektor minden komponense negatív, kell hogy legyen, tehát a sajátérték nem lehet degenerált, csak 1 sajátvektor tartozhat hozzá.
A fentiek fényében tehát:
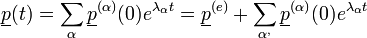
Ahol az egyenlet végén lévő szummás tagok kihalnak, mivel a 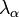 -k negatívak (egyébként a megoldás - ahogy fentebb láttuk - elszaladna a végtelenbe).
-k negatívak (egyébként a megoldás - ahogy fentebb láttuk - elszaladna a végtelenbe).
Megjegyzés: fázisátalakulásnál nagyok a fluktuációk, mivel az egész rendszer együtt változik, ellentétben a magas hőmérsékleten lévő kis fluktuációkkal. Ez a 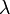 -k értékeiben azt jelenti, hogy (
-k értékeiben azt jelenti, hogy (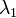 ugye mindig nulla,)
ugye mindig nulla,) 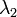 abszolútértékben nagyon kicsi, mert reciproka adja a relaxációs időt:
abszolútértékben nagyon kicsi, mert reciproka adja a relaxációs időt:
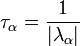
És most jöjjön egy levezetés.
Két spinből álló rendszer átmeneti valószínűségeinek meghatározása
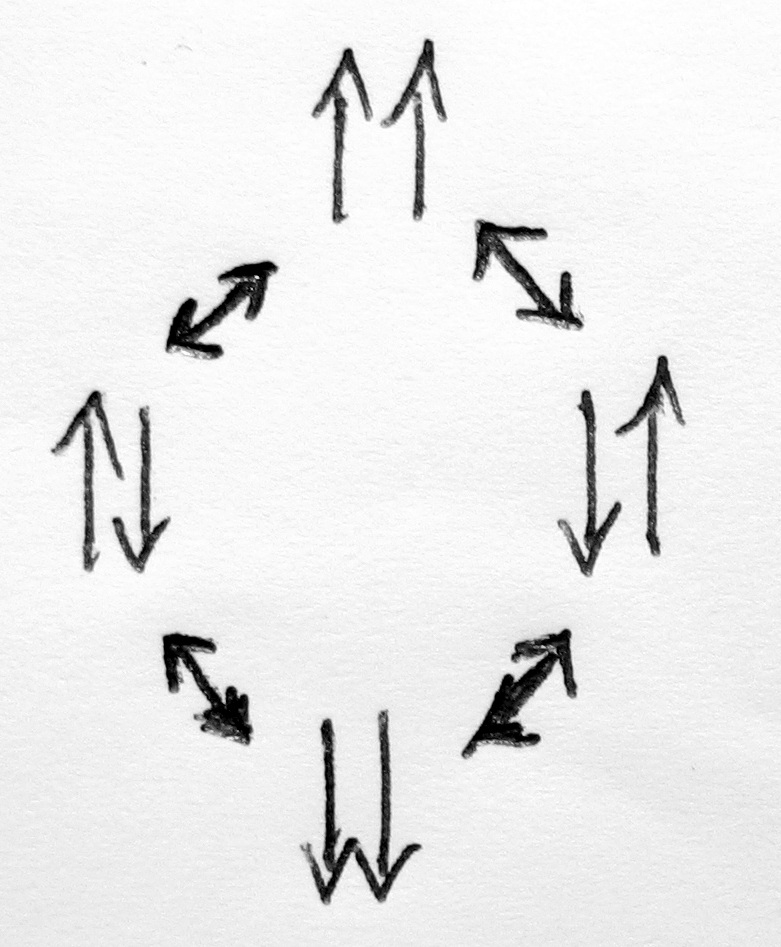
Tehát rendszerünk két spinből áll, amit egy négy elemű gráfon ábrázolhatunk.
Egyszerre csak egy spin fordulhat!
Az állapotok közötti átmeneti valószínűségek meghatározásához először az egyennsúlyi valószínűségeket kell meghatároznunk.
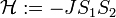 és
és 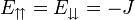 , valamint
, valamint 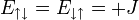
Tudjuk még továbbá, hogy:
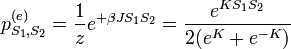 , ahol z az állapotösszeg, K pedig:
, ahol z az állapotösszeg, K pedig:
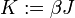 , így
, így 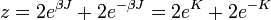
Jelölés: 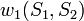 . Jelentése: bármelyik
. Jelentése: bármelyik 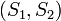 állapotban vagyunk, és az egyes(!) spint forgatjuk. Érdemes megjegyezni, hogy a
állapotban vagyunk, és az egyes(!) spint forgatjuk. Érdemes megjegyezni, hogy a 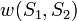 átmeneti valószínűségek 1/idő dimenziójúak.
átmeneti valószínűségek 1/idő dimenziójúak.
Ezen okból az átmeneti valószínűségek hányadosára a következő értékeket kaphajuk:
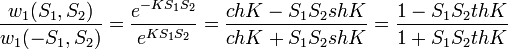
Az egyenlet bal oldalán lévő felső tört felső része annak valószínűsége, hogy 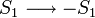 állapotátmenet történik meg, míg alsó része ennek pont az ellenkezője. Az e-ados alakokat azért lehet a fenti módon átalakítani, mert kihasználtuk, hogy a spinek csak
állapotátmenet történik meg, míg alsó része ennek pont az ellenkezője. Az e-ados alakokat azért lehet a fenti módon átalakítani, mert kihasználtuk, hogy a spinek csak 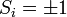 értékeket vehetnek fel.
értékeket vehetnek fel.
Végezzük el a 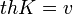 helyettesítést, ekkor a következőt kapjuk:
helyettesítést, ekkor a következőt kapjuk:
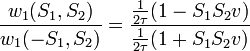 Ebből következik:
Ebből következik: 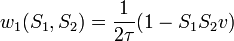
Ha 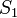 vagy
vagy 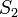 előjele változik, az egyenletben lévő előjel változik csak, azaz
előjele változik, az egyenletben lévő előjel változik csak, azaz
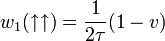 (ebből az állapotból a rendszer "nem szeret kimenni")
(ebből az állapotból a rendszer "nem szeret kimenni")
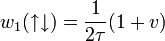 (itt a spin nagyobb valószínűséggel fordul)
(itt a spin nagyobb valószínűséggel fordul)
(v pedig mindig pozitív!)
Ugyanezt 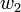 -re felírva:
-re felírva: