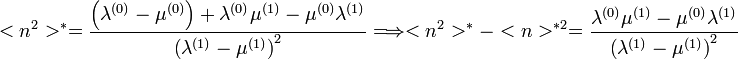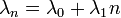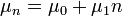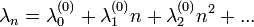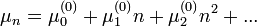VélFiz 6.tétel
Tartalomjegyzék
6. tétel: Születési-kihalási problémák
Jelölje 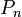 azt a valószínűséget, hogy a populációban éppen n darab élőlény él.
azt a valószínűséget, hogy a populációban éppen n darab élőlény él.
Definiáljuk a következő átmeneti valószínűségeket:
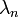 - pozitív irányba ugrunk 1-et (a populáció 1-gyel nő)
- pozitív irányba ugrunk 1-et (a populáció 1-gyel nő)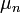 - negatív irányba ugrunk 1-et (a populáció 1-gyel csökken)
- negatív irányba ugrunk 1-et (a populáció 1-gyel csökken)
Ha n=0 egy olyan pont, melyből nem lehet kijönni, ekkor kihalt a populáció. Ettől a határfeltételtől most eltekintünk.
Ezeknek megfelelően a Master-egyenlet:
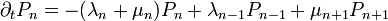
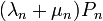 - annak valószínűésge, hogy ellép n helyről
- annak valószínűésge, hogy ellép n helyről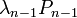 - annak valószínűésge, hogy n helyre lép
- annak valószínűésge, hogy n helyre lép 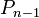 -ből
-ből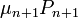 - annak valószínűésge, hogy n helyre lép
- annak valószínűésge, hogy n helyre lép 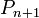 -ből
-ből
Ebben az esetben egyszerűbb a számolás, ha a generátor függvényt az eloszlás fourier transzformáltjával vezetjük be. Itt hallgatólagosan kiterjesztettük az állapotteret negatív egyedszámra is, azonban ez csupán formalizmus.
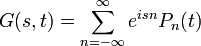
Tehát ha a Master-egyenlet mindkét oldalát szummázzuk n-szerint, és megszorozzuk 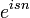 -nel, akkor megkapjuk a Generátor-függvény változását:
-nel, akkor megkapjuk a Generátor-függvény változását:
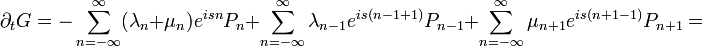
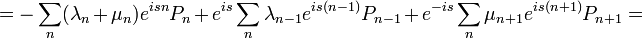
![=\sum_{n}\left[\lambda_{n}\left(e^{is}-1\right)+\mu_{n}\left(e^{-is}-1\right)\right]e^{isn}P_{n}\,](/images/math/b/e/e/bee278b711baee5cdb8d07187745dba2.png)
Stacionárius megoldás
Feltesszük, hogy az eredmény valószínűségek normalizálhatóak lesznek. Eből következik, hogy nincsen áramló megoldás, mert az végtelen idő alatt végtelenbe menne el, és nem lenne normalizálható. Ekkor teljesülni fog a részletes egyensúly:
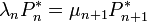
Tegyük fel, hogy 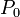 ismert (a normalizációból meghatározható). Ekkor:
ismert (a normalizációból meghatározható). Ekkor:
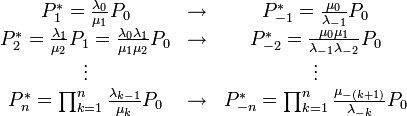
Ezek alapján a normálás:
![\partial_{t}G=P_{0}\left[1+\sum_{n=1}^{\infty}\prod_{k=1}^{n}\frac{\lambda_{k-1}}{\mu_{k}}+\sum_{n=1}^{\infty}\prod_{k=1}^{n}\frac{\mu_{-(k+1)}}{\lambda_{-k}}\right]=1](/images/math/8/3/6/8362fa7bda59f8532a7d2ef303bafcf0.png)
Ez az egyenlet megadja 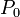 -t. Bár bonyolultak a szummák, de a stacionárius megoldást meg lehet kapni és teljesül a részletes egyensúly is.
-t. Bár bonyolultak a szummák, de a stacionárius megoldást meg lehet kapni és teljesül a részletes egyensúly is.
Lineáris folyamatok
A lineáris folyamatokat úgy definiálhatjuk, mint olyan folyamatok, ahol az egyedszámot befolyásoló halálozási és születési ráták a populáció méretétől (n) lineárisan függnek:
Ez egy speciális esete az általánosan felírható n függésnek, amit például hatványsor alakjában tekinthetünk, feltéve, hogy a sor konvergens:
Korábban már meghatároztuk a generátor-függvény időfejlődését:
![\partial_{t}G=\sum_{n}\left[\lambda_{n}\left(e^{is}-1\right)+\mu_{n}\left(e^{-is}-1\right)\right]e^{isn}P_{n}\,](/images/math/d/a/4/da4d0d8198a1428ef3ba1544b0b54a79.png)
Látható, hogy 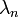 -k az
-k az 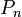 tényezővel vannak megszorozva a zárójelen kívül. Azonban
tényezővel vannak megszorozva a zárójelen kívül. Azonban 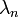 -ban szerepelnek n különböző hatványai, amik a P szorzóval éppen a különböző momentumokat adják (ha a külső szummát egy pillanatra bevisszük):
-ban szerepelnek n különböző hatványai, amik a P szorzóval éppen a különböző momentumokat adják (ha a külső szummát egy pillanatra bevisszük):
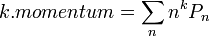
Itt k a 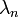 , vagy
, vagy 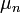 sorfejtésében az összegző index. Tehát a generátor-függvényre vonatkozó egyenletben a különböző momentumok szerpelnek különböző
sorfejtésében az összegző index. Tehát a generátor-függvényre vonatkozó egyenletben a különböző momentumok szerpelnek különböző 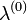 , vagy
, vagy 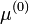 szorzókkal. Van azonban még egy exponenciális szorzó is, ezzel a generátor függvényre játszható át a kifejezés, felhasználva, hogy a momentumok a generátor-függvény deriváltjaikélnt állíthatóak elő. Összességében a születési és halálozási ráták a következőképpen írhatóak:
szorzókkal. Van azonban még egy exponenciális szorzó is, ezzel a generátor függvényre játszható át a kifejezés, felhasználva, hogy a momentumok a generátor-függvény deriváltjaikélnt állíthatóak elő. Összességében a születési és halálozási ráták a következőképpen írhatóak:
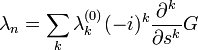
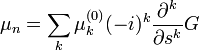
Visszaírva G időbeli változásának egyenletébe:
![\partial_{t}G=\sum_{n}\left[\sum_{k}\lambda_{k}^{(0)}(-i)^{k}\frac{\partial^{k}}{\partial s^{k}}G(e^{is}-1)+\sum_{k}\mu_{k}^{(0)}(-i)^{k}\frac{\partial^{k}}{\partial s^{k}}G(e^{-is}-1)\right]](/images/math/b/f/c/bfcd208b1f70c24034184a2f2ac1eade.png)
A következőket tekinthetjük operátoroknak, így átírhatóak a következő formába:
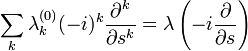
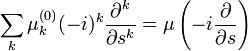
Így  -re a végleges formula:
-re a végleges formula:
![\partial_{t}G=G\sum_{n}\left[(e^{is}-1)\lambda\left(-i\frac{\partial}{\partial s}\right)+(e^{-is}-1)\mu\left(-i\frac{\partial}{\partial s}\right)\right]](/images/math/f/b/b/fbb5e8fcbfe8d5da38af6440a2b9253a.png)
(Ez tulajdonképpen egy differenciálegyenlet G-re)
Momentumok számolása
(Továbbra is lineáris folyamatokat vizsgálunk), tehát 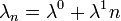 és
és 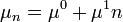
Kiindulási képletünk ismét a
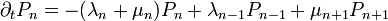
Megint szummázunk n-szerint, de most n-nel szorzunk. Így n várható értékének változását kapjuk:
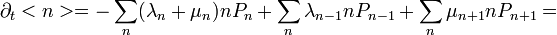
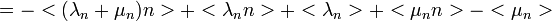
ahol 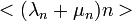 ,
, 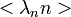 és
és 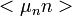 kiejtik egymást.
kiejtik egymást.
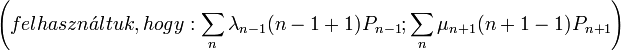
Így adódik: 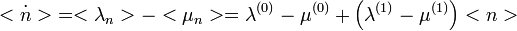 , ami egy lineáris egyenletrendszer, melynek megoldása a homogén és a partikuláris megoldások összege:
, ami egy lineáris egyenletrendszer, melynek megoldása a homogén és a partikuláris megoldások összege:
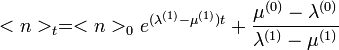
A homogén megoldásból adódik a feltétel, hogy 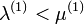 . Különben elszállna az exponens.
. Különben elszállna az exponens.
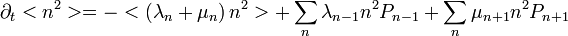
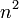 -et átírjuk a következőképp:
-et átírjuk a következőképp: 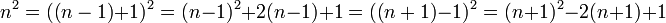 . Így:
. Így:
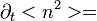
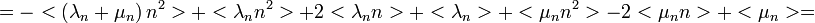
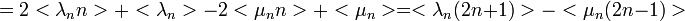
Itt újra be lehet helyettesíteni a 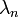 -re és
-re és 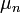 -re felírt összefüggéseket...
-re felírt összefüggéseket...
Egyensúlyban a fentiekből a következőket fogjuk kapni: