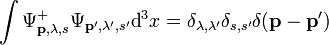Relativisztikus kvantummechanika
Ebben a részben 
Tartalomjegyzék
A Klein-Gordon egyenlet
Legyen 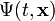 egy részecske hullámfüggvénye, mint egy inerciarendszerbeli tér- és időkoordináták skalárfüggvénye. Erre szeretnénk felírni egy kovariáns egyenletet, ami összhangban van a relativitáselmélettel. Ehhez induljunk ki a
egy részecske hullámfüggvénye, mint egy inerciarendszerbeli tér- és időkoordináták skalárfüggvénye. Erre szeretnénk felírni egy kovariáns egyenletet, ami összhangban van a relativitáselmélettel. Ehhez induljunk ki a 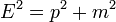 egyenletből, és helyettesítsük a fizikai mennyiségeket a klasszikus kvantummechanikából ismert operátoraikkal. Az impulzus operátora:
egyenletből, és helyettesítsük a fizikai mennyiségeket a klasszikus kvantummechanikából ismert operátoraikkal. Az impulzus operátora: 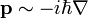 , az energiát az időderiváltnak feleltethetjük meg:
, az energiát az időderiváltnak feleltethetjük meg: 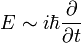 , a tömeg pedig itt is egy állandó. Így a fenti egyenletnek megfelelő operátorokat a hullámfüggvényre hattatva a következő egyenletet kapjuk:
, a tömeg pedig itt is egy állandó. Így a fenti egyenletnek megfelelő operátorokat a hullámfüggvényre hattatva a következő egyenletet kapjuk:
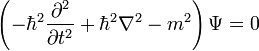
Ez a Klein-Gordon egyenlet. Ezt felírhatjuk négyesvektoros alakban is. Az energia és impulzus közötti összefüggés (diszperziós reláció) négyesvektorosan: 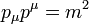 . Az előző megfeleltetés operátoroknak ekkor:
. Az előző megfeleltetés operátoroknak ekkor: 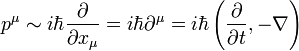 . A Klein-Gordon egyenlet ilyen alakban:
. A Klein-Gordon egyenlet ilyen alakban:
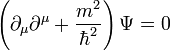
A Klein-Gordon egyenlet síkhullám megoldásait egyszerűen felírhatjuk:
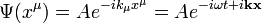
Ezt az egyenletbe behelyettesítve láthatjuk, hogy kielégíti azt, ha teljesül a 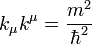 feltétel. Ez azt jelenti, hogy a
feltétel. Ez azt jelenti, hogy a 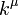 négyesvektor komponenseiből csak 3 független. Legyenek a komponensek:
négyesvektor komponenseiből csak 3 független. Legyenek a komponensek: 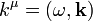 , így ezekre a
, így ezekre a 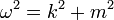 diszperziós reláció adódik. A kvantummechanikában szokásos értelmezés szerint az energia (ez az időderiválás operátor sajátértéke is)
diszperziós reláció adódik. A kvantummechanikában szokásos értelmezés szerint az energia (ez az időderiválás operátor sajátértéke is) 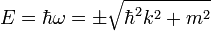 . Formálisan a pozitív energiás megoldás mellett van egy negatív energiájú is (ez jelenti majd az antirészecskéket).
. Formálisan a pozitív energiás megoldás mellett van egy negatív energiájú is (ez jelenti majd az antirészecskéket).
Eddig még nem beszéltünk arról, hogy milyen részecskék leírására alkalmas a Klein-Gordon egyenlet, felmerül a kérdés, hogy ez az egyenlet alkalmas-e a Schrödinger egyenlet relativisztikus általánosítására. Elvileg ezzel az egyenlettel 0 spinű részecskéket lehetne leírni, a valóságban azonban nincs olyan elemi részecske, amit csak a Klein-Gordon egyenlet írna le (a fotonokra felírható hullámegyenletek hasonlóak, de ott nem egy skalármező, hanem a potenciálokból álló négyesvektor komponensei szerepelnek). Ennek ellenére érdemes megvizsgálni, hogyha lennének ilyen részecskék, akkor milyen tulajdonságokkal rendelkeznének. A Schrödinger-egyenletnél a hullámfüggvény abszolútértékének négyzete megtalálási valószínűségsűrűségként volt értelmezhető. Kérdéses, hogy itt lehet-e ehhez hasonló megállapításokat tenni. Ehhez írjuk fel a Klein-Gordon egyenletet és a komplex konjugáltját:
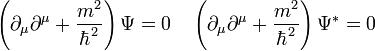
Szorozzuk meg az eredeti egyenletet (balról) 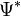 -al, a komplex konjugált egyenletet
-al, a komplex konjugált egyenletet 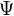 -vel, és vonjuk ki a kettőt egymásból. Az eredmény:
-vel, és vonjuk ki a kettőt egymásból. Az eredmény:
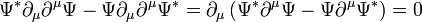
Azt kaptuk, hogy egy négyesvektor divergenciája 0. Ez lehetőséget ad egy négyesáram bevezetésére, amire egy megmaradási tétel (kontinuitási egyenlet) írható fel. Legyen:
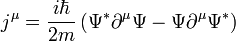
Ekkor fennáll, hogy 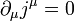 . A komponenseket
. A komponenseket 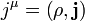 formában írva ez egy kontinuitási egyenlet jelent:
formában írva ez egy kontinuitási egyenlet jelent:
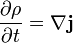
Az egész térre integrálva azt kapjuk, hogy a 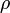 sűrűség integrálja állandó:
sűrűség integrálja állandó:
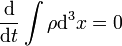
Ez alapján azt lehetne mondani, hogy 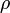 a Schrödinger egyenletnél bevezethető valószínűségsűrűséghez hasonlóan viselkedik, ennek ellenére nem lehet valószínűségsűrűségként értelmezni, mert a Schrödinger-egyenletnél használt abszolútértéknégyzettel szemben
a Schrödinger egyenletnél bevezethető valószínűségsűrűséghez hasonlóan viselkedik, ennek ellenére nem lehet valószínűségsűrűségként értelmezni, mert a Schrödinger-egyenletnél használt abszolútértéknégyzettel szemben 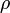 értéke nem csak pozitív lehet, hanem negatív is. Ez abból következik, hogy a Klein-Gordon egyenlet időben másodrendű, így kezdőfeltételként
értéke nem csak pozitív lehet, hanem negatív is. Ez abból következik, hogy a Klein-Gordon egyenlet időben másodrendű, így kezdőfeltételként 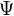 -t és az idő szerinti deriváltját tetszőlegesen lehet megválasztani, úgy is, hogy
-t és az idő szerinti deriváltját tetszőlegesen lehet megválasztani, úgy is, hogy 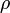 egyes helyeken negatív legyen.
egyes helyeken negatív legyen.
Így a Klein-Gordon megoldásainak nem lehet a Schrödinger-egyenletnél megszokott valószínűségi értelmezést adni. Abban az esetben viszont, ha töltött részecskékről van szó, egy töltés áramsűrűséget lehet bevezetni. Legyen ekkor:
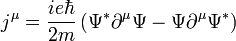
Az előző definícióhoz képest az egyetlen eltérés a részecskék töltésegységét jelentő  szorzó, így
szorzó, így 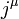 négyes áramsűrűségként értelmezhető (a kontinuitási egyenlet ugyanúgy teljesül rá). A nulladik komponense a töltéssűrűség:
négyes áramsűrűségként értelmezhető (a kontinuitási egyenlet ugyanúgy teljesül rá). A nulladik komponense a töltéssűrűség:
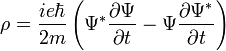
A térszerű komponensek a hármas áramsűrűséget adják:
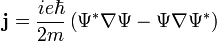
Az össztöltés megmarad:
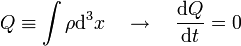
Ezzel szemben 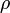 értéke egy adott pontban tetszőlegesen változhat, lehet pozitív és negatív is. Ez azt jelenti, hogy a Klein-Gordon egyenlettel nem lehet egy rögzített (pozitív vagy negatív) töltésű részecskét leírni, az időfejlődés során megjelenhetnek ellentétes töltésű tartományok, ennek magyarázata az, hogy minden részecskének létezik ellentétes töltésű antirészecskéje, és a részecskék és antirészecskék száma nem marad meg, csak az össztöltés, keletkezhetnek és annihilálódhatnak részecske-antirészecske párok. Ennek a teljes leírására azonban a Klein-Gordon egyenlet jelenlegi formája nem alkalmas, el kell végezni a
értéke egy adott pontban tetszőlegesen változhat, lehet pozitív és negatív is. Ez azt jelenti, hogy a Klein-Gordon egyenlettel nem lehet egy rögzített (pozitív vagy negatív) töltésű részecskét leírni, az időfejlődés során megjelenhetnek ellentétes töltésű tartományok, ennek magyarázata az, hogy minden részecskének létezik ellentétes töltésű antirészecskéje, és a részecskék és antirészecskék száma nem marad meg, csak az össztöltés, keletkezhetnek és annihilálódhatnak részecske-antirészecske párok. Ennek a teljes leírására azonban a Klein-Gordon egyenlet jelenlegi formája nem alkalmas, el kell végezni a 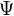 tér második kvantálását. Ezt itt nem tesszük meg, az antirészecskék jelenlétét viszont a síkhullám megoldásokon is tudjuk egyszerűen szemléltetni. Ehhez írjuk fel az előbbi síkhullám megoldást (a szokásos
tér második kvantálását. Ezt itt nem tesszük meg, az antirészecskék jelenlétét viszont a síkhullám megoldásokon is tudjuk egyszerűen szemléltetni. Ehhez írjuk fel az előbbi síkhullám megoldást (a szokásos 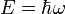 és
és 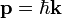 jelöléseket használva):
jelöléseket használva):
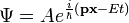
Itt 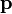 tetszőleges (hármas) vektor, és érvényes az
tetszőleges (hármas) vektor, és érvényes az 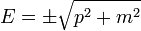 diszperziós reláció. Legyen a pozitív megoldás
diszperziós reláció. Legyen a pozitív megoldás 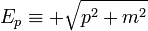 , így
, így 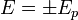 , a különböző előjelhez tartozó megoldások külön felírva:
, a különböző előjelhez tartozó megoldások külön felírva:

Az ezekből számolt töltéssűrűségek (a deriválást elvégezve):

Az egyik esetben a töltéssűrűség pozitív, a másikban negatív. Ezt úgy lehet értelmezni, hogy a 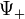 megoldás
megoldás 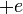 töltésű, a
töltésű, a 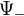 megoldás
megoldás 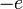 töltésű részecskéket ír le.
töltésű részecskéket ír le.
A Dirac-egyenlet
A Dirac-egyenlet bevezetése
Szeretnénk egy, a Schrödinger-egyenlethez hasonló alakú (időben elsőrendű), de a relativitáselmélettel összhangban levő egyenletet bevezetni. A Schrödinger-egyenlet ismert alakja:
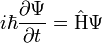
Szeretnénk, ha a Hamilton-operátor összhangban lenne a relativitáselmélet 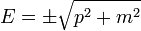 összefüggésével. Tegyük fel, hogy létezik egy ilyen operátor, ami előáll az impulzusok (térszerinti deriváltak) és a tömeg (mint számmal szorzás) lineárkombinációjaként, és a négyzetére teljesül a relativisztikus energia-impulzus összefüggés (a továbbiakban a latin betűs indexek a térszerű koordinátákat jelölik:
összefüggésével. Tegyük fel, hogy létezik egy ilyen operátor, ami előáll az impulzusok (térszerinti deriváltak) és a tömeg (mint számmal szorzás) lineárkombinációjaként, és a négyzetére teljesül a relativisztikus energia-impulzus összefüggés (a továbbiakban a latin betűs indexek a térszerű koordinátákat jelölik: 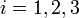 , rájuk is vonatkozik a kétszer előforduló indexre automatikus összegzés szabálya):
, rájuk is vonatkozik a kétszer előforduló indexre automatikus összegzés szabálya):

A fenti feltételeknek nincs megoldása abban az esetben, ha az 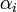 és
és 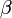 együtthatók számok, így keressük úgy a megoldást, hogy a
együtthatók számok, így keressük úgy a megoldást, hogy a 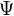 hullámfüggvény több komponensű (oszlopvektor) és az együtthatók mátrixok. Így a feltételeink:
hullámfüggvény több komponensű (oszlopvektor) és az együtthatók mátrixok. Így a feltételeink:
- Legyen
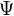 egy
egy 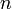 komponensű vektor, a komponenseit jelölje
komponensű vektor, a komponenseit jelölje 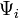
- Legyen a
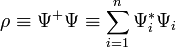 mennyiség egy megmaradó 4-es áram nulladik komponense
mennyiség egy megmaradó 4-es áram nulladik komponense
- Teljesüljön a relativisztikus
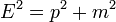 összefüggés. Ez azt jelenti, hogy
összefüggés. Ez azt jelenti, hogy 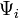 minden komponense kielégíti a Klein-Gordon egyenletet
minden komponense kielégíti a Klein-Gordon egyenletet
- Legyen az egyenlet kovariáns, azaz teljesítse azt a feltételt, hogy mindkét oldalán a Lorentz-transzformációk szempontjából ugyanúgy transzformálódó mennyiségek szerepelnek
Megmutatható, hogy ezek a feltételek az együtthatómátrixokra a következő egyenleteket adják:
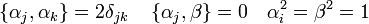
A kapcsos zárójelek az antikommutátorokat jelentik. Ezeket az egyenleteket legkevesebb 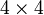 -es mátrixokkal lehet kielégíteni, léteznek magasabb dimenziójú megoldások is, mi a továbbiakban csak az
-es mátrixokkal lehet kielégíteni, léteznek magasabb dimenziójú megoldások is, mi a továbbiakban csak az 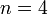 esettel foglalkozunk. Ebben az esetben a megoldás (igazából több megoldás lehetséges, de ezek nem függetlenek egymástól, így elég csak egyet vizsgálni):
esettel foglalkozunk. Ebben az esetben a megoldás (igazából több megoldás lehetséges, de ezek nem függetlenek egymástól, így elég csak egyet vizsgálni):
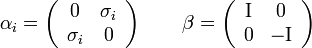
Itt 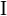 a
a 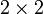 -es egységmátrix, a
-es egységmátrix, a 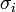 mátrixok a Pauli-mátrixok. A komponensek kiírva:
mátrixok a Pauli-mátrixok. A komponensek kiírva:
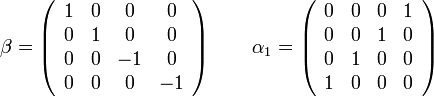
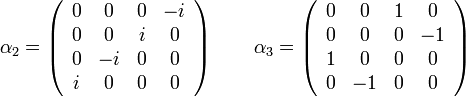
A 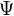 hullámfüggvény pedig egy négy komponensű vektor lesz. Nagyon fontos megjegyeznünk, hogy
hullámfüggvény pedig egy négy komponensű vektor lesz. Nagyon fontos megjegyeznünk, hogy 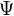 nem négyesvektor (a relativitáselméletben bevezetett módon), a komponenseit nem lehet a négyesvektorokra ható Lorentz-mátrixokkal transzformálni, matematikailag
nem négyesvektor (a relativitáselméletben bevezetett módon), a komponenseit nem lehet a négyesvektorokra ható Lorentz-mátrixokkal transzformálni, matematikailag 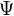 egy másik tér eleme. A továbbiakban az együtthatómátrixok és
egy másik tér eleme. A továbbiakban az együtthatómátrixok és 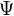 komponenseinek az indexeit általában elhagyjuk, azok között a mátrixalgebrában szokásos műveletek érvényesek. Az
komponenseinek az indexeit általában elhagyjuk, azok között a mátrixalgebrában szokásos műveletek érvényesek. Az 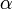 mátrixok indexei a mátrix sorszámát jelentik. Egyes esetekben nehéz számontartani a különböző fajta vektorok komponenseit, a lényeg az, hogy a differenciáloperátorok
mátrixok indexei a mátrix sorszámát jelentik. Egyes esetekben nehéz számontartani a különböző fajta vektorok komponenseit, a lényeg az, hogy a differenciáloperátorok 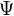 minden komponensére külön hatnak, egy együtthatómátrix pedig a mátrixszorzás szabályai szerint hat. A Dirac-egyenlet így felírva:
minden komponensére külön hatnak, egy együtthatómátrix pedig a mátrixszorzás szabályai szerint hat. A Dirac-egyenlet így felírva:
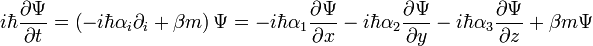
A jobboldali összeg minden tagjában a deriválás 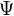 minden komponensére külön hat, majd az
minden komponensére külön hat, majd az 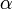 mátrixokkal szorzás a komponensek között hat a szokásos mátrixszorzási szabályok szerint.
mátrixokkal szorzás a komponensek között hat a szokásos mátrixszorzási szabályok szerint.
A Dirac-egyenlet kovariáns alakja
Szorozzuk be a Dirac-egyenlet korábban megkapott alakját a 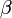 mátrixxal és rendezzük úgy, hogy az egyik oldalon 0 legyen. Így kapjuk a Dirac-egyenlet kovariáns alakját:
mátrixxal és rendezzük úgy, hogy az egyik oldalon 0 legyen. Így kapjuk a Dirac-egyenlet kovariáns alakját:
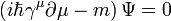
Ehhez bevezettük a Dirac-mátrixokat:
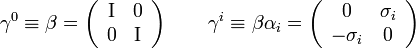
A komponensek kiírva:
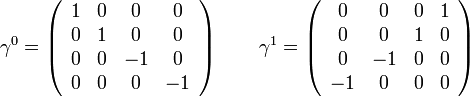
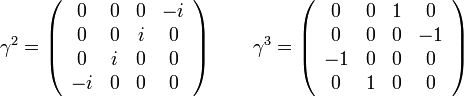
A Dirac-mátrixok tulajdonságai:
- Mindegyik mátrix unitér
-
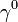 hermitikus
hermitikus
-
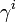 antihermitikusak (
antihermitikusak (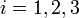 )
)
- fennáll az antikommutátor reláció:
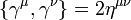
Megjegyzés: A fenti tulajdonságok használhatóak a Dirac-mátrixok definiálására. Az összefüggések megoldása nem egyértelmű, de bármely négy mátrix, ami teljesíti a követelményeket megfelelő a fizikai leíráshoz (a mátrixok matematikailag unitér ekvivalensek, ugyanazt a fizikát írják le).
Megjegyzés 2: Az irodalomban gyakran használt jelölés: Értelmezés sikertelen (Hiányzó <code>texvc</code> végrehajtható fájl; a beállítást lásd a math/README fájlban.): \partialslash \eqiuv \gamma^{\mu} \partial_{\mu}
(itt egy áthúzott parciális d betűvel kellene jelölni a 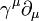 szorzatot)
szorzatot)
Definiáljuk a hullámfüggvény Dirac-konjugáltját:
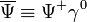
Itt a 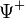 transzponált azt a sorvektort jelenti, aminek az elemei
transzponált azt a sorvektort jelenti, aminek az elemei 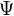 elemeinek a komplex konjugáltjai, így a Dirac-konjugált is egy sorvektor. Ezzel bevezethetjük a Dirac-egyenlethez tartozó négyes áramsűrűséget:
elemeinek a komplex konjugáltjai, így a Dirac-konjugált is egy sorvektor. Ezzel bevezethetjük a Dirac-egyenlethez tartozó négyes áramsűrűséget:
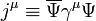
Ennek a komponensei a Dirac-indexek (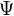 komponensei) szempontjából skalárok lesznek (a definícióban minden komponensnél egy sorvektor, egy mátrix és egy oszlopvektor szorzata szerepel, ennek az eredménye egy szám). Viszont belátható, hogy a Lorentz-transzformációk szempontjából
komponensei) szempontjából skalárok lesznek (a definícióban minden komponensnél egy sorvektor, egy mátrix és egy oszlopvektor szorzata szerepel, ennek az eredménye egy szám). Viszont belátható, hogy a Lorentz-transzformációk szempontjából 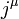 négyesvektorként viselkedik, a
négyesvektorként viselkedik, a 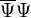 mennyiség pedig négyesskalár.
mennyiség pedig négyesskalár.
Felmerül a kérdés, hogy 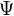 oszlopvektor hogyan transzformálódik egy Lorentz-transzformációt végezve. Mégegyszer hangsúlyozzuk, hogy
oszlopvektor hogyan transzformálódik egy Lorentz-transzformációt végezve. Mégegyszer hangsúlyozzuk, hogy 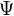 nem egy négyesvektor (csak "véletlenül" van pont négy komponense), így nem lehet összeszorozni egy Lorentz-mátrixxal. Lehetne gondolni, hogyha
nem egy négyesvektor (csak "véletlenül" van pont négy komponense), így nem lehet összeszorozni egy Lorentz-mátrixxal. Lehetne gondolni, hogyha 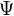 -nek semmi köze sincs a négyesvektorokhoz, akkor nem transzformálódik, de ez sem igaz; minden
-nek semmi köze sincs a négyesvektorokhoz, akkor nem transzformálódik, de ez sem igaz; minden 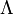 Lorentz-transzformációhoz létezik egy
Lorentz-transzformációhoz létezik egy 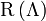
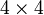 -es mátrix, ami a hullámfüggvény komponenseit transzformálja a mátrixszorzás szabályai szerint:
-es mátrix, ami a hullámfüggvény komponenseit transzformálja a mátrixszorzás szabályai szerint:
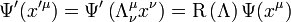
A Dirac-egyenlet transzformálásánál belátható összefüggések:
- Az egységmátrixnak megfelelő transzformáció az egységmátrix:
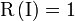
- A transzformációk szorzása "asszociatív":
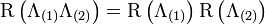
- Az inverz "bevihető":
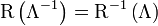
- Feltehetjük, hogy a Dirac-mátrixok nem transzformálódnak (belátható, hogy választhatóak így)
- A deriválás operátor négyesvektorként transzformálódik:
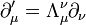
Ezekből levezethető a transzformációs mátrixot meghatározó egyenlet:
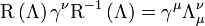
Ennek a megoldásaként (ami nem teljesen triviális, ezért itt mellőzzük) megkaphatnánk a hullámfüggvényt transzformáló mátrixot.
Megjegyzés: Ha csoportelméleti megfontolásokból indulunk ki, akkor azt kapjuk, hogy a négykomponensű hullámfüggvény, illetve a négyesvektorok a Lorentz-transzformációk csoportjának a különböző ábrázolásaihoz tartozó objektumok, a transzformációkra általános módszer adható, amiből a Lorentz-mátrixokat és a hullámfüggvényt transzformáló mátrixokat is meg lehet kapni.
A Dirac-egyenlet síkhullám megoldásai
Írjuk fel a Dirac-egyenletet a Schrödinger-egyenlethez hasonló alakban:
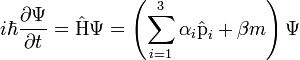
(Itt 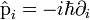 )
Keressük a stacionárius megoldásokat
)
Keressük a stacionárius megoldásokat 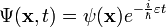 alakban. Így a Schrödinger-egyenletnél megszokotthoz hasonlóan energiasajátérték egyenletet kapunk. Bontsuk fel a négykomponensű hullámfüggvényt két kétkomponensű vektorra:
alakban. Így a Schrödinger-egyenletnél megszokotthoz hasonlóan energiasajátérték egyenletet kapunk. Bontsuk fel a négykomponensű hullámfüggvényt két kétkomponensű vektorra:
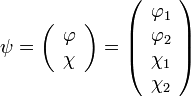
Ezekre egy csatolt egyenletrendszert kapunk:
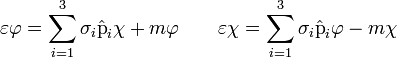
A síkhullám megoldás:
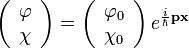
Ezt behelyettesítve egy homogén lineáris egyenletrendszert kapunk, ami tartalmazza a 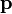 és
és  paramétereket:
paramétereket:
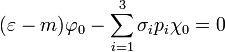
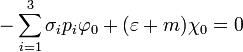
A megoldás feltétele, hogy a determináns 0 legyen. Felhasználva a Pauli-mátrixokra ismert 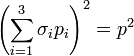 azonosságot, a feltétel:
azonosságot, a feltétel:
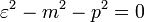
Ez az energiára az ismerős összefüggés. Látszik az is, hogy léteznek pozitív és "negatív" energiájú megoldások (részecskék és antirészecskék). Az egyenletrendszerből:
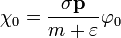
Legyen 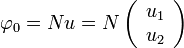 úgy, hogy
úgy, hogy 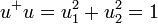 és
és 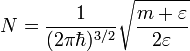 a normálás miatt. Legyen
a normálás miatt. Legyen 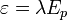 , ahol
, ahol 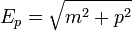 és
és 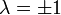 , ekkor a megoldást
, ekkor a megoldást 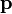 és
és 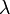 paraméterezik. Ezekkel felírva:
paraméterezik. Ezekkel felírva:
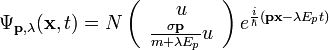
A hullámfüggvény normálása:
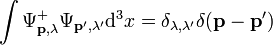
A fenti megoldásban van még két szabad paraméter, az 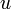 vektor komponensei. Ez azt fejezi ki, hogy a részecske spinjének az iránya még nincs meghatározva. A spinoperátor:
vektor komponensei. Ez azt fejezi ki, hogy a részecske spinjének az iránya még nincs meghatározva. A spinoperátor:
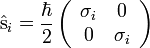
Vezessük be a helicitásoperátort:
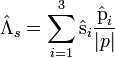
Ez a spinnek az impulzus irányára vett vetületét adja meg. Válasszuk meg az 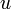 vektort úgy, hogy a helicitásoperátor sajátvektora legyen. Tekintsünk egy, a
vektort úgy, hogy a helicitásoperátor sajátvektora legyen. Tekintsünk egy, a 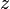 tengely irányába mozgó részecskét, ekkor a helicitásoperátor:
tengely irányába mozgó részecskét, ekkor a helicitásoperátor:
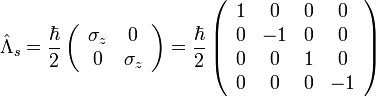
A sajátértékek: 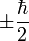
A sajátvektorok:
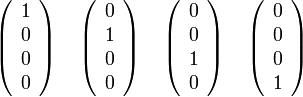
A teljes megoldás így:
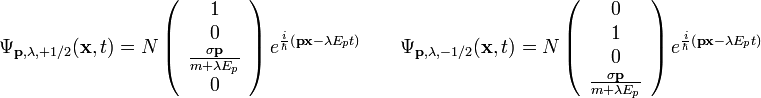
A normálás ekkor: