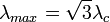Mintázat 4.óra

Bevezető

Használt jelölések:

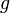$g$: gravitációs gyorsulás

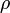$\rho$: sűrűség

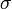$\sigma$: felületi feszültség

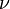$\nu$: kinematikai viszkozitás

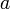$a$: tipikus méret

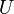$U$: sebesség

Folyadékdinamikát leíró fontos paraméterek, fogalmak

Reynold-szám (pl. lamináris-turbulens átmenet jellemzése áramlásoknál):

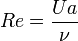$Re=\frac{Ua}{\nu}$ (inercia/viszkozitás)

Froude-szám (a Mach-szám folyadékdinamikai megfelelője):

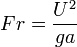$Fr=\frac{U^2}{ga}$ (inercia/gravitáció)

Eötvös- vagy Bond- szám (cseppek, kapillárisok leírása):

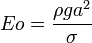$Eo=\frac{\rho ga^2}{\sigma}$ (gravitáció/görbület)

a kapilláris hossz:

$l_c=\sqrt{\frac{\sigma}{\rho g}}$

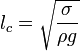
Weber szám (két folyadék határfelületén lezajló jelenségek jellemzésére):

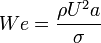$We=\frac{\rho U^2a}{\sigma}$ (inercia/görbület)

Kapilláris szám (porózus anyagba folyadékot préselünk):

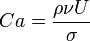$Ca=\frac{\rho \nu U}{\sigma}$ (viszkozitás/görbület)

Konvektív az az instabilitás, ahol a perturbáció egy áramlási vonal mentén előrehaladva erősödik fel, de a keletkezés helyén nem, abszolút instabilitás esetén az áramlás nem tudja elmosni a zajt, helyben erősödik fel, általában globálisan megfigyelhető.

Perturbációszámítás dióhéjban

Mivel az előadáson az hangzott el, hogy csak a fő lépéseket kell tudni, ezért ezeket próbáltam meg kivonatolni:

Ha van egy egyensúlyi rendszerünk, akkor egy tetszőleges változóra (legyen ez most 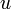$u$) arra rárakhatunk egy időben le- vagy felcsengő, térben periódikus perturbációt:

$u'=u+\tilde{u}$

$\tilde{u} = \varepsilon e^{\omega t+ikr}$

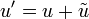
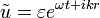
Egy változó megperturbálása más változók perturbációját is maga után vonhatja (pl. a felület megváltoztatása okozhat nyomásváltozást), itt feltételezzük, hogy a perturbációk hasonló alakúak. Majd ezt behelyettesítjük a rendszert leíró diffegyenletekbe, csak a lineáris tagokat hagyjuk meg, ez meghatároz egy 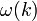$\omega(k)$ függvényt. Ezek után megnézzük, hogy milyen 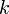$k$ értékek esetén kapunk pozitív 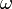$\omega$-t. Ezek közül is az a módus fogja dominálni a kapott mintázatot, amelyik a legnagyobb mértékben nő fel, ezt pedig deriválással könnyen meghatározhatjuk.

Ha kevés lenne, amit ide leírtam, feltételnül egészítsétek ki!!!

Határfelületi instabilitások

Rayleigh-Taylor instabilitás

(Ide tartozik D. Sharp, Physica D-ben megjelent cikke)

Ez az instabilitás abban az esetben jön létre, amikor egy kisebb sűrűségű folyadék fölé egy nagyobb sűrűségűt rétegzünk (pl. a plafonon száradó festék, illetve forgó rendszerben történhet hasonló instabilitás). Itt egy fonots paraméter, a sűrűségkontraszt, vagy Atwood szám:

$A=\frac{\rho_H-\rho_L}{\rho_H+\rho_L}$

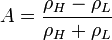
ahol 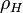$\rho_H$ a sűrűbb, 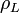$\rho_L$ a ritkább anyag sűrűsége. Egy 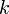$k$ hullámhosszú harmónikus perturbáció amplitúdóját a következő egyenlet írja le:

$\ddot{\eta}(t)=\alpha^2(k)\cdot \eta(t)$

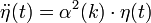
ahol a növekedési ráta:

$\alpha^2(k)=G\left(\frac{\rho_H-\rho_L}{\rho_H+\rho_L}\right)k-\left(\frac{\sigma}{\rho_H+\rho_L}\right)k^3$

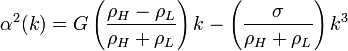
Itt 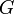$G$ a felületre merőleges gyorsulás. A felületi feszültség simító hatása miatt egy kiritkus 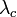$\lambda_c$ hullámhossznál rövidebb perturbációk elhalnak, mert 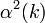$\alpha^2(k)$ negatív lesz:

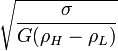
$\sqrt{\fra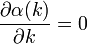c{\sigma}{G(\rho_H-\rho_L)}}$

A $\frac{\partial\alpha(k)}{\partial k}=0$ feltételből pedig megkapjuk a leggyorsabban növő módust:

$\lambda_{max}=\sqrt{3}\lambda_c$

Nem-newtoni folyadékok

<<<Vissza az óra nyitólapjára