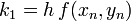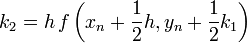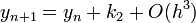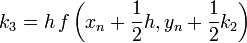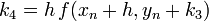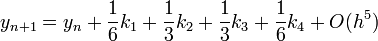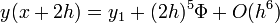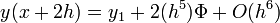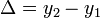„Numerikus módszerek” változatai közötti eltérés
| 53. sor: | 53. sor: | ||
==Egyenletrendszerek megoldása== | ==Egyenletrendszerek megoldása== | ||
| + | |||
| + | ===Gauss-Jordan elimináció=== | ||
| + | |||
| + | ===LU dekompozíció=== | ||
| + | |||
| + | ===Singular Value Decomposition - Szinguláris érték dekompozíció === | ||
| + | Sokszor előfordul, hogy a mátrix, amit invertálni akarunk, közel van a szingulárishoz (det A ≈ 0), és sem a Gauss-elimináció, se az LU felbontás nem jár sikerrel. | ||
| + | |||
| + | Adott egy ''A'' mátrixunk, ami MxN méretű. Ezt a mátrixot felírhatjuk UWV<sup>T</sup> formában, ahol: | ||
| + | * U: MxN, oszlop-ortogonális mátrix | ||
| + | * W: NxN, diagonális, a szinguláris értékeket tartalmazza | ||
| + | * V<sup>T</sup>: NxN, ortogonális mátrix | ||
| + | A módszer segítségével nem-négyzetes mátrixokat is tudunk invertálni (''pszeudoinverz'') a következő módon: | ||
| + | |||
| + | <math>A^{-1} = V\,[diag(1/w_j)]\,U^T</math> | ||
| + | |||
| + | Ami problémát okozhat, az a szinguláris értékek reciproka, ha az nulla, vagy nagyon közel van nullához. A megoldás, hogy ebben az esetben az 1/w<sub>j</sub>-t nullának vesszük. | ||
==Optimalizációs módszerek - szélsőérték keresés== | ==Optimalizációs módszerek - szélsőérték keresés== | ||
===Konjugált gradiens módszer=== | ===Konjugált gradiens módszer=== | ||
| + | |||
===Szimulált hőkezelés=== | ===Szimulált hőkezelés=== | ||
| − | A módszer elnevezése az anyagtudomány területéről ered, ahol hőkezelési eljárásokkal lehet változtatni egy anyag kristályosodási méretét. Számítógépes módszerként egy | + | A módszer elnevezése az anyagtudomány területéről ered, ahol hőkezelési eljárásokkal lehet változtatni egy anyag kristályosodási méretét. Számítógépes módszerként egy sokdimenziós függvény energiaminimumának megkeresésére lehet használni. |
Működési struktúra: | Működési struktúra: | ||
A lap 2011. június 9., 14:08-kori változata
Tartalomjegyzék
Diffegyenlet-megoldó módszerek
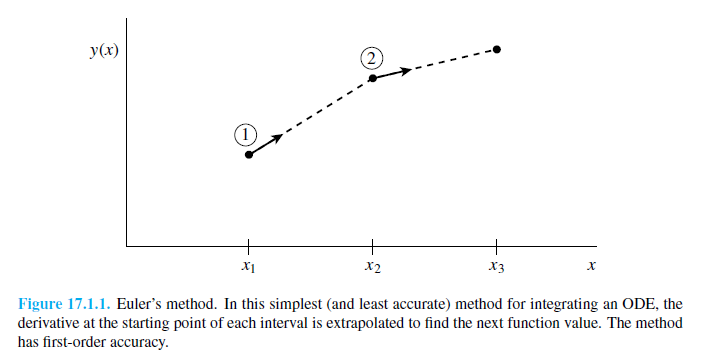
Euler-módszer
A legegyszerűbb egylépéses módszer. Az y(x=0)=y0 kezdőfeltétellel megadott, y’=f(x,y) diffegyenlet megoldása esetén az Euler lépés alakja (Taylor-sorfejtés első két tagja):
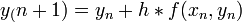
Hibája: Taylor-sorfejtést tovább írjuk, a különbség 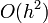 lesz. Használata nem javasolt, mert a hibák hamar felösszegződnek, a megoldás „felrobban”. Ennek elkerülésére érdemes lehet használni az implicit Euler-módszert:
lesz. Használata nem javasolt, mert a hibák hamar felösszegződnek, a megoldás „felrobban”. Ennek elkerülésére érdemes lehet használni az implicit Euler-módszert: 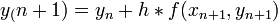 . Ez nagy h értékekre is stabil marad.
. Ez nagy h értékekre is stabil marad.
Runge-Kutta módszer
Miért használjuk? Mert sokkal pontosabb, mint az Euler-módszer.
Másodrendű RK (vagy midpoint method - középponti módszer)
Ez a módszer tehát harmadrendig pontos. Általánosan az n-ed rendű RK-nak 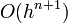 hibája van.
hibája van.
Negyedrendű RK
A negyedrendű módszerben négyszer kell kiértékelni az f függvényt, míg az Euler-módszernél egyszer kellett. Ezért ennek a használata akkor gazdaságos, ha ugyanakkora pontosság mellett legalább négyszer akkora lehet a lépésköz.
Adaptív RK
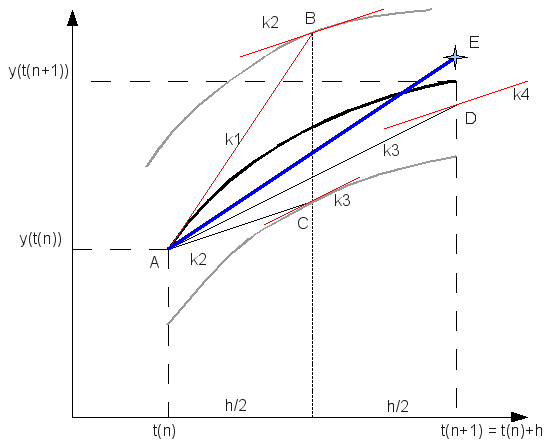
Egy differenciálegyenlet megoldása során lehetnek gyorsan és lassan változó szakaszok a függvényben. A lassan változó szakaszok integrálása során nagyobb lépéseket is tehetünk a hiba növekedése nélkül. Ennek a megoldására szolgál az adaptív Runge-Kutta módszer. Alapötlete, hogy egy lépést tegyünk meg egyszer teljesen (2h-val, 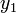 ), egyszer pedig két fél lépésben (h-val,
), egyszer pedig két fél lépésben (h-val, 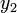 ). Mindegyik lépés 4 függvény kiértékelést igényel (3*4), de ebből kettő megegyezik, így 11 kiértékelés szükséges a 2*4 helyett, ami a két fél lépésből jönne össze.
). Mindegyik lépés 4 függvény kiértékelést igényel (3*4), de ebből kettő megegyezik, így 11 kiértékelés szükséges a 2*4 helyett, ami a két fél lépésből jönne össze.
A kettő közti különbség:
A különbség 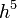 -nel skálázik. Ha egy
-nel skálázik. Ha egy 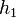 lépés eredménye
lépés eredménye 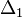 , és mi
, és mi 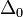 hibát akarunk elérni, akkor
hibát akarunk elérni, akkor 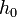 lépést kell tennünk, ami:
lépést kell tennünk, ami:
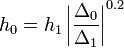
Ha 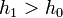 , akkor meg kell ismételni a számolást egy kisebb lépéssel, ha pedig
, akkor meg kell ismételni a számolást egy kisebb lépéssel, ha pedig 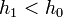 , akkor a következő lépésben használhatjuk
, akkor a következő lépésben használhatjuk 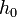 -t lépésként.
-t lépésként.
Egyenletrendszerek megoldása
Gauss-Jordan elimináció
LU dekompozíció
Singular Value Decomposition - Szinguláris érték dekompozíció
Sokszor előfordul, hogy a mátrix, amit invertálni akarunk, közel van a szingulárishoz (det A ≈ 0), és sem a Gauss-elimináció, se az LU felbontás nem jár sikerrel.
Adott egy A mátrixunk, ami MxN méretű. Ezt a mátrixot felírhatjuk UWVT formában, ahol:
- U: MxN, oszlop-ortogonális mátrix
- W: NxN, diagonális, a szinguláris értékeket tartalmazza
- VT: NxN, ortogonális mátrix
A módszer segítségével nem-négyzetes mátrixokat is tudunk invertálni (pszeudoinverz) a következő módon:
![A^{-1} = V\,[diag(1/w_j)]\,U^T](/images/math/b/e/2/be29f4083659602a3acf54303900924a.png)
Ami problémát okozhat, az a szinguláris értékek reciproka, ha az nulla, vagy nagyon közel van nullához. A megoldás, hogy ebben az esetben az 1/wj-t nullának vesszük.
Optimalizációs módszerek - szélsőérték keresés
Konjugált gradiens módszer
Szimulált hőkezelés
A módszer elnevezése az anyagtudomány területéről ered, ahol hőkezelési eljárásokkal lehet változtatni egy anyag kristályosodási méretét. Számítógépes módszerként egy sokdimenziós függvény energiaminimumának megkeresésére lehet használni.
Működési struktúra:
- Válasszunk egy tetszőleges kezdőállapotot (i)
- Válasszuk ki az egyik szomszédot (j)
- Ha a szomszéd energiája kisebb, átlépünk rá
- Ha nagyobb a szomszéd energiája, az energiakülönbség, és egy globális T paraméter által meghatározott valószínűség szerint elfogadjuk a nagyobb energiájú helyet
Az elfogadási valószínűségek tehát:
- ha f(j) ≤ f(i), akkor 1
- ha f(j) > f(i), akkor
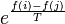
A T hőmérsékletet kezdetben nagynak választva, majd folyamatosan csökkentve ezzel a módszerrel megtalálhatjuk a függvény globális minimumát.