VélFiz 3.tétel
Tartalomjegyzék
3. tétel: Master-egyenlet diszkrét állapottérben, stacionáris állapotok
Inkább Langevin gondolatvilágából következik (formalizmusában viszont inkább Einsteint követi).
Alapvetése
- Megfigyelek valamit, amit valamilyen háttér befolyásol.
- A háttér annyira nem fontos, csak a hatása a megfigyelt részecskére (van néhány kiválasztott szabadsági fokom).
- Mivel a háttérről nem sokat tudok, valószínűségi egyenletekkel dolgozom.
Példa
Van egy rendszerem, amiből engem csak a mágneses viselkedés érdekel, csak a spineket figyelem.
Nagy rendszer: sok spin 
Két részecskéből álló rendszer esetén a teljes állapottér négy diszkrét állapotból áll:
A Master-egyenlet felírása
Most legyen n diszkrét állappot.
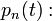 mi annak a valószínűsége, hogy a rendszer az n-edik állapotban van?
mi annak a valószínűsége, hogy a rendszer az n-edik állapotban van?
- Tegyük fel, hogy tudom, hogy egységnyi idő alatt mi annak a valószínűsége, hogy a rendszer n-ből m állapotba megy át.
Ennek jelölése: 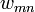 --> nem tudunk róla semmit, de tegyük fel, hogy ismerjük az értékét.
--> nem tudunk róla semmit, de tegyük fel, hogy ismerjük az értékét.
- Fermi aranyszabály:
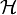 ismert,
ismert, 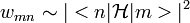 QM-ben.
QM-ben.
Ising [1] spin-rendszer esetén: 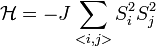 , ahol
, ahol 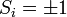 [1][2]
[1][2]
- Tegyük fel, hogy a folyamat Markov-folyamat, tehát létezik olyan
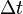 , hogy már csak a t mondja meg, hogy mi történik
, hogy már csak a t mondja meg, hogy mi történik 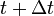 -ben. (És tegyük fel, hogy az átmenetek megvalósulnak.)
-ben. (És tegyük fel, hogy az átmenetek megvalósulnak.)
Ekkor:
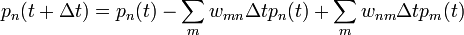
A 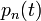 -t ismerem, a
-t ismerem, a 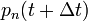 -t keresem, a
-t keresem, a 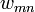 és
és 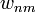 egységnyi időre vonatkozik.
egységnyi időre vonatkozik.
Sorbafejtek 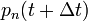 körül,
körül, 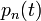 kiesik, így:
kiesik, így:
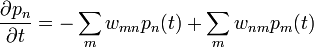
A Master-egyenlet diszkrét állapottérben
Ennek kell, hogy legyen stacionárius megoldása, amihez relaxál:
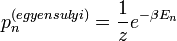 , ahol
, ahol 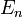 az n-edik állapot energiája.
az n-edik állapot energiája.
Ha ezt helyettesítem be, akkor a bal oldal 0 lesz-->ez 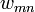 és
és 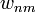 -re megkötés!
-re megkötés!
Van időtükrözési invariancia is! Ennek következménye a részletes egyensúly (bővebben később).
Példa
Szilárd testekben lévő spinrendszereknél a többi kölcsönhatás hőtartályként adódik a rendszerhez. (Pl. szupravezetésnél feltételezték, hogy az elektronok Coulomb-kölcsönhatása le van árnyékolva, a fononok pedig a háttér hőtartályt adják. Később kiderült, hogy alacsony hőmérsékleten éppen a fononok miatt kezdik el vonzani egymást az elektronok.)
- ↑ A ferromágnes első modellje. A spinek egy irányba szeretnek beállni, de a hőmozgás szétválasztja őket. T->0: Curie-hőmérséklet alatt ferromágneses viselkedés.
- ↑ A Fermi aranyszabály és az Ising spin-rendszer csak a spineket vizsgálja, nálunk meg egy csomó más hatás is van, tehát nem pont azt írják le, ami nekünk kell.

