Vita:A klasszikus mechanika elméleti tárgyalása

A virtuális munka elve általános esetben csak annyit mond ki, hogy a szabaderők virtuális munkája nem pozitív egyensúlyban.

Olyan esetben mondható, hogy a virtuális munka zérus, amikor minden 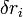$\delta r_i$ virtuális elmozdulásra igaz, hogy a -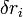$\delta r_i$ virtuális elmozdulást is megengedik a kényszerfeltételek.

Lásd például Mechanika I. 131.§

Ez már az előző tételnél is pontatlanul van írva.

Gyula

A virtuális munka levezetésénél feltettük, hogy a kényszerek olyan alakban írhatóak, hogy:

$\phi( r_1, r_2, ..., r_N ) = 0\,$

A Mechanika I. könyvben negativitásra vezető kényszererő a kötél kényszere azonban nem fogalmazható meg így, hiszen ott a kényszer akkor hat, ha a két végének a távolsága nagyobb vagy egyenlő a kötél hosszánál. Másképp fogalmazva a kötél kényszerereje nem analitikus függvénye a kooridnátáknak. Ennek ellenére, ha megpróbáljuk megengedni a kötél irányával szembeni elmozdulást, és kiszámoljuk a kényszererők munkáját az nulla lesz, hiszen az ideális kötélet infinitezimálisan összenyomva az már nem fejt ki erőt, tehát a kényszererő zérus. Ekkor a szabaderők virtuális munkája valóban negatív lenne... azonban ekkor a rendszer nincs egyensúlyban, mi pedig az egyensúly feltételét keressük. Összességében jelenleg nem látok indokot a negatív jel bevezetésére itt, hiszen egyensúlyban ez nem igaz a munkákra. Jeffrey 2009. június 21., 16:12 (UTC)

Akkor viszont szerintem ezt a feltételt oda kellene írni, már csak azért is, mert a kényszerek gradienses alakja is csak ebben az esetben érvényes. Erre nem tudok jó irodalmat írni, de mi pl. Csikornál vettünk olyan eseteket, amikor a kényszerek nem csak a helykoordináktól, hanem az időderiváltaktól, vagy közvetlenül az időtől is függenek, és ilyenkor újabb tagok jönnek be. Nem tudom ugyan, hogy ezekbe mennyire fognak belemenni a vizsgán, de szerintem azért nem árt tisztában lenni vele, hogy ez nem a legáltalánosabb eset.

Megjegyzés a második szerkesztésedhez: A kényszererők virtuális munkája mindig zérus. Ezt is tekinthetjük egy axiómának, aminek a segítségével például a Newton-egyenletből levezethető a d'Alembert-elv A kötelet is akkor kezeljük kényszerként, ha nyújthatatlannak tekintjük, vagyis a kötél két végének távolsága nem lehet nagyobb a kötél hosszánál. A virtuális munka elve végig a szabaderőkről szól, és azt a pontot vizsgáljuk, amelyikből indulnak a virtuális elmozdulások vektorai, nem pedig azt, ahova mutatnak. Tehát természetes, hogy amikor az egyensúlyi helyzetet vizsgáljuk, akkor a virtuális elmozdulás révén a rendszer "kimozdul" az egyensúlyi helyzetből, de pont ezért "virtuális elmozdulás", mert ez ténylegesen nem történik meg. Gyula

Igazad van beírtam a szócikkhez, a második részben meg valóban hülyeséget irtam az előbb. Ennek ellenére a köteles példánál leragadva: létezik olyan rendszer és olyan kényszerek, hogy a negatív munkát is figyelembe kell venni az egyensúly teljesüléséhez? Hirtelen az jut az eszembe, hogy egy testet két kötéllel kötünk ki, amelyek egymással szemben hatnak, de ebben az esetben a kényszerek helyettesíthetőek egy fenti analitikus kényszerrel, és ugyanúgy megoldhatóak a negativitás feltétele nélkül.Jeffrey 2009. június 21., 18:16 (UTC)

Hát nem egészen értem mit értesz az alatt, hogy "figyelembe kell venni", de a legegyszerűbb, amit el tudok képzelni, egy 1D-s eset, amikor mondjuk egy függőleges csőben mozgó golyót veszünk. A cső alja legyen bezárva, így alul van az egyensúlyi helyzet. A kényszerek által megengedett egyetlen lehetséges virtuális elmozdulás a függőlegesen fölfelé mutató vektor, erre pedig negatív a virtuális munka, tehát erre biztosan nem tudsz olyan egyenletet felírni, amiben 0 virtuális munka szerepel.