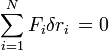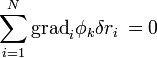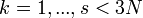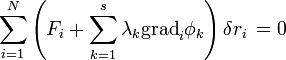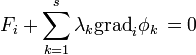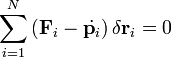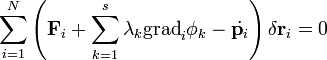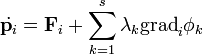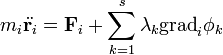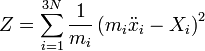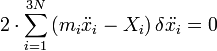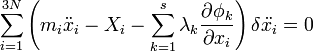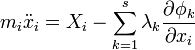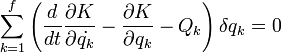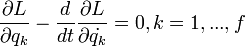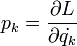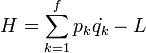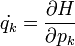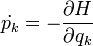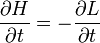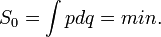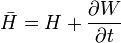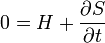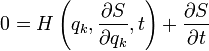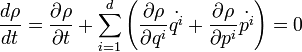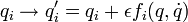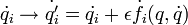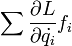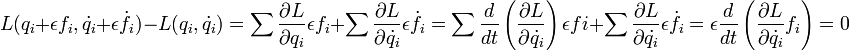A klasszikus mechanika elméleti tárgyalása
Tartalomjegyzék
- 1 A mechanika elvei
- 2 A virtuális munka elve
- 3 d'Alembert elv és a Lagrange-féle elsőfajú egyenletek
- 4 A Gauss-féle legkisebb kényszer
- 5 Általános koordináták és a Lagrange-féle másodfajú mozgástörvény
- 6 Hamilton-féle variációs elv és az Euler-Lagrange egyenletek
- 7 Kanonikus egyenletek, Hamilton-függvény
- 8 Ciklikus koordináták, kanonikus transzformáció
- 9 Maupertuis-elv (*)
- 10 A Hamilton-Jacobi egyenlet
- 11 A Liouville-tétel(*)
- 12 Megmaradási tételek, mint szimmetriák következményei
A mechanika elvei
A klasszikus mechanika alapvető törvényeinek megfogalmazását Newton megtette. Azonban ugyanezek az elvek megfogalmazhatóak számos, a Newton-i axiómákkal ekvivalens, azonban matematikailag más alakban, ami sokszor szemléletesebb, illetve egyszerűbb tud lenni. Ezek a mechanika elvei, amelyek nem bizonyítható axiómák, ezek helyességét a tapasztalatok adják.
A virtuális munka elve
Vegyünk egy N anyagi pontból álló mechanikai rendszert, amelynek koordinátái 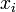 ,
, 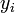 ,
, 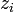 , a ható erőt pedig
, a ható erőt pedig 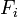 jelöli. Legyen
jelöli. Legyen 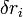 az i-edik anyagipontnak a kényszerek által megengedett infinitezimális és virtuális elmozdulása. Itt a virtuális alatt azt értjük, hogy nem tartozik ezen elmozulásokhoz időtartam. A tárgyalt rendszer akkor lesz egyensúlyban, ha a ható erők virtuális munkája zérus:
az i-edik anyagipontnak a kényszerek által megengedett infinitezimális és virtuális elmozdulása. Itt a virtuális alatt azt értjük, hogy nem tartozik ezen elmozulásokhoz időtartam. A tárgyalt rendszer akkor lesz egyensúlyban, ha a ható erők virtuális munkája zérus:
Szabad mozgás esetén minden 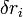 tetszőleges, tehát az erővektoroknak kell zérusnak lenniük. Ha van N pontunk, akkor azokhoz 3N darab koordináta tartozik, és ennél kevesebb kényszerfeltétel lehet adott, különben nincs mozgás. Itt most feltesszük, hogy a kényszereink egy felületre korlátozzák a rendszert, és ezért alakjuk így írható:
tetszőleges, tehát az erővektoroknak kell zérusnak lenniük. Ha van N pontunk, akkor azokhoz 3N darab koordináta tartozik, és ennél kevesebb kényszerfeltétel lehet adott, különben nincs mozgás. Itt most feltesszük, hogy a kényszereink egy felületre korlátozzák a rendszert, és ezért alakjuk így írható:
A kényszerfeltételek a virtuális elmozdulások alatt is kell, hogy teljesüljenek, ebből valamint egy infinitezimális elmozduláshoz tartozó Taylor-sorfejtésből belátható, hogy a kényszerfeltételek a kövektező általános alakba írhatóak:
Ezeket a Lagrange-multiplikátorok módszerével vehetjük figyelembe: egy ismeretlen 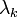 szorzóval hozzáadjuk őket a virtuális munka egyenlethez:
szorzóval hozzáadjuk őket a virtuális munka egyenlethez:
Most a szabad esettel szemben csak (3N-s) darab együttható lesz zérus, de a többinél a Lagrange-multiplikátorokat választjuk úgy, hogy a maradék együtthatók is eltűnjenek. Ekkor úgy tekinthetjük, mintha a virtuális elmozdulások függetlenek lennének, ezért az egyenlőség teljesüléséhez az erők összegének kell zérusnak lennie, ezért:
A második tagot elnevezhetjük kényszererőknek, és ekkor a az egyensúly feltétele, hogy a szabad és kényszererők összege zérus legyen. A 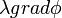 -s definícióból az is látható, hogy felületen mozgásnál a kényszererő merőleges a felületre (mivel grad
-s definícióból az is látható, hogy felületen mozgásnál a kényszererő merőleges a felületre (mivel grad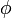 a felületi normális irányába mutat).
a felületi normális irányába mutat).
d'Alembert elv és a Lagrange-féle elsőfajú egyenletek
Jean le Rond d'Alembert a virtuális munka elvéhez hasonló kifejezést vezetett be, de az nem csak az egyensúlyt írja le, hanem egyben mozgástörvény is:
A mechanikai rendszer az elv értelmében úgy mozog, hogy a fenti kifejezés minden időpillanatban teljesül. Szabad rendszerre ez a Newton mozgásegyenletet adja, hiszen tetszőleges :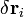 -re el kell tűnnie a zárójelnek, azaz
-re el kell tűnnie a zárójelnek, azaz 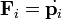 .
Ha kényszerek is jelen vannak, akkor ismér a Lagrange-multiplikátoros átalakítást végezzük el:
.
Ha kényszerek is jelen vannak, akkor ismér a Lagrange-multiplikátoros átalakítást végezzük el:
A virtuális munka elvéhez hasonlóan itt is formálisan függetlenként kezelhetők a megváltozások, így
Ha feltesszük, hogy a tömeg állandó, akkor 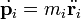 , tehát:
, tehát:
Ezt az egyenletet nevezzük a Lagrange-féle elsőfajú egyenleteknek (N darab van belőlük). Mivel ezek vektor egyenletek, így tulajdonképpen 3N darab egyenletünk van, és ezenkívül az s darab kényszeregyenlet. Ez éppen annyi, mint az ismeretlenek száma: 3N darab térkoordináta az idő függvényében, és az s darab multiplikátor.
A Gauss-féle legkisebb kényszer
Gauss bevezette a kényszer mértékét:
Itt 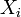 szabaderő. A zárójelben tehát a szabad mozgástól való eltérés áll a kényszerek hatására. Gauss elve a következőt mondja: a kényszerek által megengedett gyorsulásváltozások közül a legkisebb valósul meg. Variációs módszerrel alakítható ez tovább, amikoris csak a gyorsulást variáljuk. Holonom-szkleronom kényszerekre
szabaderő. A zárójelben tehát a szabad mozgástól való eltérés áll a kényszerek hatására. Gauss elve a következőt mondja: a kényszerek által megengedett gyorsulásváltozások közül a legkisebb valósul meg. Variációs módszerrel alakítható ez tovább, amikoris csak a gyorsulást variáljuk. Holonom-szkleronom kényszerekre 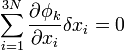 . Ez időderiválás után:
. Ez időderiválás után: 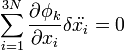 .
Ugyanakkor a kényszert is megvariáljuk:
.
Ugyanakkor a kényszert is megvariáljuk:
Ehhez hozzáadva a szokásos módon Lagrange multiplikátorral a kényszereket:
Ismét a megszokott módon a megválasztás független, illetve ahol nem, ott a Lagrange együtthatókat választjuk meg, tehát:
Általános koordináták és a Lagrange-féle másodfajú mozgástörvény
Az eddigi tárgyalásokban a kényszerek, mint független egyenletek voltak figyelembe véve. Ha azonban olyan koordinátákra térünk át, amelyek illeszkednek a kényszerekhez, akkor ezekben ezek a feltételek eltűnnek, így egyszerűbb alakot kapunk a mozgásegyenletekre. Az állítás az, hogy ilyen transzformációk léteznek, az ilyen áttéréssel kapott új koordinátákat általános koordinátáknak nevezzük, és 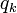 -val jelöljük, az általános sebességeket pedig
-val jelöljük, az általános sebességeket pedig 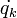 -val. Itt kell megjegyezni, hogy ezek nem feltétlen hosszúság illetve sebesség dimenziójú változók.
-val. Itt kell megjegyezni, hogy ezek nem feltétlen hosszúság illetve sebesség dimenziójú változók.
A koordináta transzformációs függvények deriváltjaival és kis megváltozásaival átírható a d'Alembert-elv varióciós módszerrel. Ha bevezetjük a 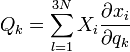 általánosított erőt, amely nem feltétlen erő dimenziójú, de a
általánosított erőt, amely nem feltétlen erő dimenziójú, de a 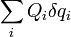 munka dimenziójú. Továbbá bevezetjük a mozgásienergiát:
munka dimenziójú. Továbbá bevezetjük a mozgásienergiát: 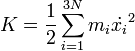 . Ezekkel átírva a d'Alembert-elv a következő alakú lesz:
. Ezekkel átírva a d'Alembert-elv a következő alakú lesz:
Itt f a szabadsági fokok száma (a 3N szabadság az s darab kényszerrel csökkentve). A tetszőleges variáció miatt:
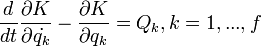
Ezek a Lagrange-féle másodfajú mozgásegyenletek. Ha az erők konzervatívak, akkor felírhatók potenciál deriváltjaként, és ekkor minden K helyére K-V írandó, amelyet elnevezhetünk Lagrange-függvénynek, így a képlet a jól ismert alakot ölti:
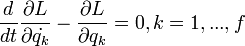
Ezek felhasználásával általános módszert adhatunk a mechanikai problémák megoldására: Ismerjük fel a rendszert jellemző általános koordinátákat, és írjuk fel a transzformációs függvényeket. Az így definiált általános koordinátákkal fejezzük ki a potenciált (V), az általános sebességekkel pedig a kinetikus energiát (K). Végül írjuk fel a Lagrange-függvényt (L = K - V), és belőle a Lagrange-féle másodfajú mozgásegyenleteket. Az így kapott mozgásegyenlet pedig elvileg megoldható.
Hamilton-féle variációs elv és az Euler-Lagrange egyenletek
A Hamilton által kimondott variációs elv, az eddigieken azért mutat túl, mert nem csupán a mechanikai problémák általános megfogalmazásában használható, hanem az optika és a kvantummechanika törvényeit is egyszerűen meg lehet általa fogalmazni. Konzervatív rendszerre az állítás a következő:
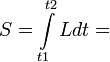 extrémum
extrémum
Itt S a hatás, L a Lagrange-függvény. Az állítás az, hogy ebből 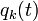 meghatározható. A problémát variációszámítási módszerekkel lehet megoldani, amely egy funkcionált szélsőértékbe vívő függvényeket határozza meg. Ez pont az itteni probléma, hiszen a Lagrange az általánosított koordinátáktól, sebességektől és esetleg az időtől függ, és mi az általánosított koordinátákat keressük. A variációs módszerből adódó egyenletk a következőek:
meghatározható. A problémát variációszámítási módszerekkel lehet megoldani, amely egy funkcionált szélsőértékbe vívő függvényeket határozza meg. Ez pont az itteni probléma, hiszen a Lagrange az általánosított koordinátáktól, sebességektől és esetleg az időtől függ, és mi az általánosított koordinátákat keressük. A variációs módszerből adódó egyenletk a következőek:
Ezek az Euler-Lagrange egyenletek.
Kanonikus egyenletek, Hamilton-függvény
Az eddig használt Lagrange leírásban másodrendű differenciálegyenletket kaptunk. Az úgynevezett kanonikus egyenletek azzel szemben elsőrendű differenciálegyenleteket szolgáltatnak, amelyek a másodrendűekkel egyenértékűek, azonban kétszer annyi van belőlük. Bevezetjük a kanonikusan konjugált impulzust:
És bevezetjük a Hamilton-függvényt:
Az Euler-Lagrange egyenletek figyelembevételével, és a Hamilton-függvény teljes differenciájának felhasználásával kapjuk a kanonikus egyenleteket:
Továbbá:
Ha a rendszer konzervatív, és az általánosított koordinátákra való áttérés időfüggetlen, akkor a Hamilton-függvény a mechanikai energiát adja. Ennek a formalizmusnak kiemelkedő szerepe van a kvantummechanika és a kvantumtéreleméletek tágyalásánál.
Ciklikus koordináták, kanonikus transzformáció
Ha a Hamilton-függvény nem függ valamely koordinátától, akkor az ahhoz a koordinátához tartozó konjugált impulzus állandó a kanonikus egyenletek miatt, és azonnal megoldást szolgáltat a mozgásegyenletre (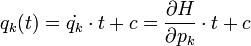 ). Az ilyen tulajdonságú koordinátát ciklikus koordinátának nevezzük.
Értelemszerűen minél több ciklikus kooridnátánk van, annál egyszerűbb megoldani az adott problémát. Ezért érdemes foglalkozni azokkal a transzformációkkal, amelyek változatlanul hagyják a kanonikus egyenleteket, de ciklikus koordinátákra térhetünk át segítségükkel. Ezek a transzformációk tehát olyan koordináták között visznek át, amelyek teljesítik a kanonikus egyenletket továbbá a variációs elvnek is eleget tesznek (a kanonikus egyenletek is abból származtathatóak). Ezek alapján belátható, hogy a variált funkcionálban van egy szabadságunk egy tetszőleges függvény időszerinti deriváltjának erejéig. Ezt a függvény nevezzük alkotó függvénynek, mert segítségével kifejezhetőek a transzformációs szabályok. Az alapján, hogy az alkotó függvényt melyik két változóval fejezzük ki a négy (régi és új koordináta, régi és új impulzus) közül, különböző összefüggéseket kapunk a koordináták és az alkotó függvény között, valamint megkapjuk a Hamilton-függvény transzformácóját is.
). Az ilyen tulajdonságú koordinátát ciklikus koordinátának nevezzük.
Értelemszerűen minél több ciklikus kooridnátánk van, annál egyszerűbb megoldani az adott problémát. Ezért érdemes foglalkozni azokkal a transzformációkkal, amelyek változatlanul hagyják a kanonikus egyenleteket, de ciklikus koordinátákra térhetünk át segítségükkel. Ezek a transzformációk tehát olyan koordináták között visznek át, amelyek teljesítik a kanonikus egyenletket továbbá a variációs elvnek is eleget tesznek (a kanonikus egyenletek is abból származtathatóak). Ezek alapján belátható, hogy a variált funkcionálban van egy szabadságunk egy tetszőleges függvény időszerinti deriváltjának erejéig. Ezt a függvény nevezzük alkotó függvénynek, mert segítségével kifejezhetőek a transzformációs szabályok. Az alapján, hogy az alkotó függvényt melyik két változóval fejezzük ki a négy (régi és új koordináta, régi és új impulzus) közül, különböző összefüggéseket kapunk a koordináták és az alkotó függvény között, valamint megkapjuk a Hamilton-függvény transzformácóját is.
Maupertuis-elv (*)
A Maupertuis-elv energiamegmaradó rendszerekre vonatkozik, vagyis a Lagrange-függvény nem függ explicite az időtől. Az elv kimondja, hogy a rendszer által megtett út olyan, hogy a rövidített hatás
ahol az integrált a pályára vett vonalintegrálként kell érteni.
A Hamilton-Jacobi egyenlet
A mozgásegyenletek megoldhatóak egy szélsőséges tanszformációval is, amennyiben a a Hamilton-függvényt zérusra transzformáljuk. Ekkor mind a koordináták, mind az impulzusok deriváltjai nullával egyenlőek a kanonikus egyenletek értelmében. A Hamilton-függvényre vonatkozó transzformációs egyenlet az alkotófüggvénnyel kifejezve a következő:
Mivel a végső Hamiltonnak zérust szeretnénk, ezzel a feltétellel egy speciális alkotófüggvényt definiálhatunk, amely a következő egyenletet elégíti ki:
A Hamilton-függvény a koordináták, az impulzus és az idő függvénye lehet. Ezek közül az alkotó függvénnyel az impulzus is kifejezhető, ezért:
Ez a Hamilton-Jacobi egyenlet, és S a hatásfüggvény, amelyet már korábban bevezettünk a Hamilton-féle variációs elvnél. A Hamilton-Jacobi egyenlet abban különbözik az eddigiektől, hogy parciális differenciálegyenlet, ezért határfeltételek is kellenek hozzá, és nehezebb megoldani, ennek ellenére ha nem közvetlenül a mozgásegyenletet akarjuk megkapni, csak összefüggéseket a hatás és a koordináták között, akkor sokfelé jól használható.
A Liouville-tétel(*)
A Hamilton-i mechanikai rendszerekre kimondható a Liouville-tétel, ami azt fogalmazza meg, hogy nem-disszipatív rendszerre a fázistérfogat állandó marad. Ha 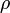 a fázistérbeli eloszlás függvény, és a rendszer d dimenziós:
a fázistérbeli eloszlás függvény, és a rendszer d dimenziós:
Ez azért fontos egyenlet, mert nem csak egyensúlyi szituációkban használható, hanem sokrészecskés bonyolult dinamikai problémákra is, ezért alapvető fontosságú a statisztikus jelenségek tárgyalásában.
Megmaradási tételek, mint szimmetriák következményei
A közismert és a klasszikus mechanikában előbukkanó megmaradási tételek igen egyszerűen következnek a Hamilton-függvényes formailzmusból.
Impulzusmegmaradás
Az impulzusmegmardás a tárgyalási koordinátarendszer eltolásával szembeni invarianciából vezethető le. Ez tulajdonképpen a tér homogenitása: mindegy hogy hova tesszük a mechanikai rendszert, a Hamiltonja ugyanaz, és az események ugyanúgy zajlanak.
Impulzusmomentum megmaradása
Az impulzusmomentum megmaradása a koordinátarendszer elforgatásával szembeni invarianciából vezethető le. Ez tulajdonképpen a tér izotrópiája: mindegy hogy hogyan forgatjuk el a mechanikai rendszert, a Hamiltonja ugyanaz, és az események ugyanúgy zajlanak.
Energiamegmaradás
Ez az időbeli eltolásból következik, azaz mindegy, hogy egy adott kísérletet mikor végzünk el, a lefolyása ugyanaz, a Hamiltonja ugyanaz.
Noether-tétel(*)
A Noether-tétel azt mondja, hogy a Lagrange-függvény szimmetriáihoz hogyan lehet megmaradó mennyiséget rendelni.
Állítás:Ha a Lagrange-függvénynek szimmetriája a:
akkor a következő mennyiség megmaradó:
Bizonyítás: