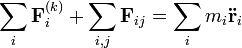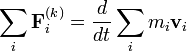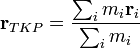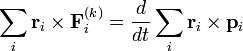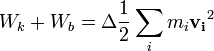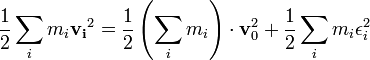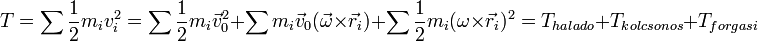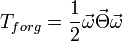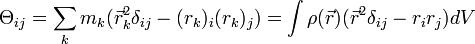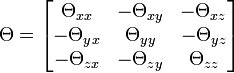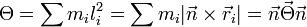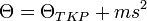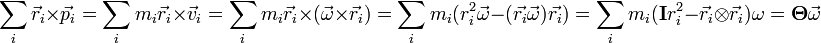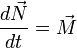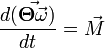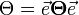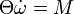A klasszikus mechanika alapjai
Tartalomjegyzék
- 1 Mérés, mértékegységek, dimenzióanalízis[1]
- 2 Kinematikai alapfogalmak, mozgás leírása különböző koordinátarendszerekben[2]
- 3 Newton törvények, statika, dinamika, erőfogalom, mozgásegyenlet, tehetetlen és súlyos tömeg, Eötvös-kísérlet
- 4 Gyorsuló koordinátarendszerek, tehetetlenségi erők
- 5 Jelenségek a forgó Földön
- 6 Munka tétel
- 7 Pontrendszerek
- 8 Merev testek
Mérés, mértékegységek, dimenzióanalízis[1]
Mérés
A fizikai fogalmakat (út, idő, sebesség, tömeg stb.) mérhető mennyiségekkel tesszük egyértelművé (egzakttá). A mérés általában valamilyen önkényesen megválasztott egységgel történő összehasonlítás. A mérés eredményét a mértékegység és a mérőszám együtt fejezi ki. Azt, hogy milyen mennyiség mértékegységéről van szó, az illető mennyiség mértékével, dimenziójával adjuk meg (például a sebesség dimenziója a hosszúság dimenziójának és az idő dimenziójának a hányadosa). A mértékegység megválasztása megállapodás kérdése.
Mértékegységek
Ebben a szakaszban főleg az SI mértékegységrendszerben használt alap mértékegységekre (alapmennyiségekre), illetve azok definícióira térnék ki. A mértékegységre definíciót az előző szakaszban láthattunk. Alapmennyiségnek nevezzük azokat a mértékegységeket, melyek nem vezethetők vissza korábban értelmezett mértékegységekre. Amelyek visszavezethetők, azokat származtatott mennyiségeknek hívjuk. A fizikai mennyiségek összessége a mértékegységrendszer, melynek alapját az alapmennyiségek képezik. Megállapodás kérdése, hogy mit választunk alapmennyiségnek.
A mértékegységek egységesítésére tett legsikeresebb próbálkozás az SI (Systéme International d'Unités) nemzetközi mértékegységrendszer. Alapmennyiségei: hosszúság, idő, tömeg, elektromos áramerősség, termodinamikai hőmérséklet, anyagmennyiség, fényerősség. Az SI mértékegységrendszer az alapmennyiségekből, kiegészítő mennyiségekből, és az egységek többszörösét vagy törtrészét kifejezni segítő prefixumokből (előtagokból) áll.
SI alapmennyiségek
| Az idő mértékegysége a másodperc, jele: s. A másodperc az alapállapotú cézium-133 atom két hiperfinom energiaszintje közötti átmenetnek megfelelő sugárzás 9 192 631 770 periódusának időtartama. |
A hosszúság mértékegysége a méter, jele: m. A méter annak az útnak a hosszúsága, melyet a fény vákuumban 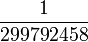 másodperc alatt megtesz. másodperc alatt megtesz.
|
| A tömeg mértékegysége a kilogramm, jele: kg. A kilogramm az 1889. évben Párizsban megtartott 1. Általános Súly- és Mértékügyi Értekezlet által a tömeg nemzetközi etalonjának elfogadott, a Nemzetközi Súly- és Mértékügyi hivatalban, Sévres-ben őrzött platina-irridium henger tömege. |
A villamos áramerősség mértékegysége az amper, jele: A. Az amper olyan állandó villamos áram erőssége, mely két egyenes, párhuzamos, végtelen hosszúságú, elhanyagolhatóan kicsiny kör keresztmetszetű és egymástól 1 méter távolságban, vákuumban elhelyezkedő vezetőben fenntartva, e két vezető között méterenként 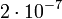 newton erőt hoz létre. newton erőt hoz létre.
|
A termodinamikai hőmérséklet mértékegysége a kelvin, jele: K. A kelvin a víz hármaspontja termodinamikai hőmérsékletének 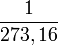 -szorosa. -szorosa.
|
| Az anyagmennyiség mértékegysége a mól, jele: mol. A mól annak a rendszernek az anyagmennyisége, amely annyi elemi egységet tartalmaz, mint ahány atom van 0,0012 kilogramm szén-12-ben. (A mól alkalmazásakor meg kell határozni az elemi egység fajtáját; ez atom, molekula, ion, elektron, más részecske vagy ilyen részecskék meghatározott csoportja lehet.) |
A fényerősség mértékegysége a kandela, jele: cd. A kandela az olyan fényforrás fényerőssége adott irányban, amely 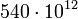 hertz frekvenciájú monokromatikus fényt bocsát ki és sugárerőssége ebben az irányban hertz frekvenciájú monokromatikus fényt bocsát ki és sugárerőssége ebben az irányban 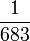 -ad watt per szteradián. -ad watt per szteradián.
|
SI kiegészítő mennyiségek
1 fok a teljes szögnek 360-ad része. 1 fok = 60 szögperc, 1 szögperc = 60 szögmsodperc. 1 radián annak a középponti szögnek a nagysága, melynek ívhossza egyenlő a kör sugarával. A szög ívmértékben kifejezett nagysága: 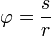 , ahol s a körív hossza, r a kör sugara. A teljes szög ívmértékben 2
, ahol s a körív hossza, r a kör sugara. A teljes szög ívmértékben 2 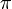 , mivel a sugár a kör kerületére 2
, mivel a sugár a kör kerületére 2 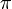 -szer mérhető fel.
360 fok = 2
-szer mérhető fel.
360 fok = 2 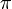 radián.
radián.
A térszöget szteradiánban mérjük (jele: sr). A szteradián a gömbsugár négyzetével egyenlő területű gömbfelületrészhez tartozó középponti térszög. Képlete: 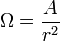 , ahol A a gömbfelületrész területe, r a gömb sugara. A teljes térszög a következő formula alapján adható meg:
, ahol A a gömbfelületrész területe, r a gömb sugara. A teljes térszög a következő formula alapján adható meg: 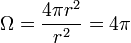
SI prefixumok
A következő prefixumok használatosak 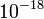 -tól
-tól 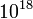 -ig sorrendben felírva, két szomszédos prefixum között 1000-szeres a különbség:
atto, femto, piko, nano, mikro, milli, egy(ség), kilo, mega, giga, tera, peta, exa.
-ig sorrendben felírva, két szomszédos prefixum között 1000-szeres a különbség:
atto, femto, piko, nano, mikro, milli, egy(ség), kilo, mega, giga, tera, peta, exa.
Dimenzióanalízis
A mérések célja a vizsgált jelenségek minél pontosabb megismerése. A mérés többször elvégezhető, különböző személyek által reprodukálható, ezáltal az adott jelenséget irányító törvények megismeréséhez kerülhetünk egyre közelebb. A törvényszerűségek megfogalmazása többnyire matematikai képletekkel, egyenletekkel történik. A jelenség megértését az eredményekből kapott törvényszerűségek elméleti értelmezése teszi teljessé.
A kísérletezés és az adatkiértékelés során nagyban megkönnyítjük saját dolgunkat, ha figyelembe vesszük, hogy a legtöbb fizikai mennyiség mérőszámmal és mértékegységgel rendelkezik, s a különböző fizikai törvényeket leíró egyenletek két oldalán álló kifejezéseknek azonos dimenziójúnak kell lennie. A fizikai mennyiségek dimenzióját úgy értelmezzük, hogy mint az adott mennyiség mérésekor használatos alapmennyiségek összességét. A mechanikával kapcsolatos problémákban leggyakrabban a hosszúság (L), tömeg (M) és idő (T) dimenzió szerepel. A származtatott mennyiségek (pl. v - sebesség, F - erő, 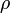 - sűrűség) dimenziója minden esetben az alapdimenziók hatványának szorzataként jelenik meg:
- sűrűség) dimenziója minden esetben az alapdimenziók hatványának szorzataként jelenik meg:
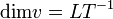 ,
, 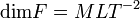 ,
, 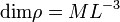 .
.
Legyen x bizonyos 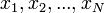 paraméterek X függvénye, azaz:
paraméterek X függvénye, azaz: 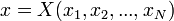 .
.
A paraméterek közül néhány kísérletileg is változtatható. A fenti függvénykapcsolat feltérképezése jelenti a fizikai törvény megismerését, a rá vonatkozó matematikai összefüggések felállítását. A fizikai törvények gyakran hatványalakban jelennek meg. Ekkor: 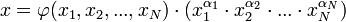 alakú, ahol
alakú, ahol 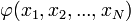 dimenzió nélküli függvény. A fenti egyenletből tehát a dimenziókra vonatkozóan a következő egyenletet kapjuk:
dimenzió nélküli függvény. A fenti egyenletből tehát a dimenziókra vonatkozóan a következő egyenletet kapjuk:
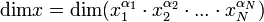 .
.
Mechanikai mennyiségek esetén: 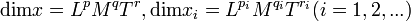
A fenti egyenletbe történő behelyettesítés után: egyrészt: 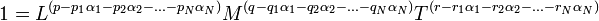 ,
,
másrészt:
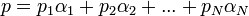
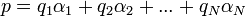
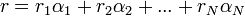
egyenletekre jutunk. (Az alapegységek dimenziói a vektortér bázisvektoraihoz hasonlóan viselkednek.) A fenti lineáris egyenletrendszerben az ismeretlenek az 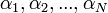 mennyiségek. Az egyenletrendszernek általában több megoldása van, ezek közül lehet kiválasztani azokat, melyek fizikailag reálisan írják el a keresett törvényt. Ez a dimenzióanalízis alapgondolata, mellyel bizonyos sejtések tartalmilag reális formában fogalmazhatók meg.
mennyiségek. Az egyenletrendszernek általában több megoldása van, ezek közül lehet kiválasztani azokat, melyek fizikailag reálisan írják el a keresett törvényt. Ez a dimenzióanalízis alapgondolata, mellyel bizonyos sejtések tartalmilag reális formában fogalmazhatók meg.
Kinematikai alapfogalmak, mozgás leírása különböző koordinátarendszerekben[2]
Kinematikai alapfogalmak
- A mozgás az ember legősibb élménye. A mozgás során a testek egymáshoz viszonyított helyzete változik.
- Ahhoz, hogy egy test mozgását leírhassuk, célszerű kiválasztani egy másik testet - vonatkoztatási rendszert - , amelyhez viszonyítva megadjuk a szóban forgó test hely-, illetve helyzetváltozását. Vonatkoztatási rendszer lehet például a tanterem, mint rögzített test, amelyhez viszonyít leírjuk a kísérletekben felhasznált testek mozgásást.
- Az anyagi pont mozgását vonatkoztatási rendszerhez rögzített koordiánta-rendszerben írjuk le. A koordiántarendszer kezdőpontjából (origójából) az anyagi ponthoz húzott szakaszt (amely időfüggő is) r helyvektornak nevezzük, r(t)-vel jelöljük.
- Pálya: az a görbe, amelyet az anyagi pont mozgása során leír.
- A pálya teljes hosszának, vagy egy részének hossza az út, jele: s.
- A pálya két, kezdő- és végpontját összekötő irányított szakasz az elmozdulás, jele:
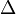 r. Az elmozdulás hossza általában nem egyezik meg a két pont között megtett út hosszával.
r. Az elmozdulás hossza általában nem egyezik meg a két pont között megtett út hosszával. - A pálya alakja függ a vonatkoztatási rendszertől (pl. egy a megfigyelt anyagi ponthoz képest mozgó vonatkoztatási rendszerben egész más alakú a pálya, mint egy nem mozgóban).
- A sebesség általánosított definíciója: tetszőleges görbén mozgó test esetén képezzük az elmozdulás és a közben eltelt idő hányadosát:
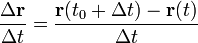 .
.
Ebből pillanatnyi sebesség: 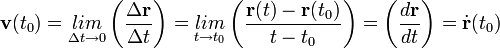
A fentiekben a helyvektorból vezettük le a sebesség definícióját. Most vezessük le az elmozdulás-vektorból:
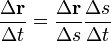 .
.
Belátható, hogy a fenti képlet jobb oldalának első tagja az egységnyi hosszúságú érintő irányú t (tangenciális) vektorhoz tart, míg a bal oldalát egyszerűen v-vel jelölhetjük. A fentiekből látható, hogy a helyvektorból és az elmozdulásvektorból számolt pillanatnyi sebesség közötti összefüggés:
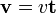 .
.
Egy mozgó pont sebessége derékszögű koordináta-renszerben: 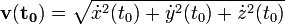 .
.
- A gyosrulás általánosított definíciója: tegyük fel, hogy v(t) sebességet minden időpillanatban ismerjük. Ekkor a pillanatnyi gyorsulásvektor:
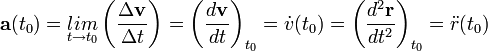
A gyorsulás meghatározása derékszögű koordináta-rendszerben: 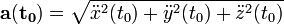 .
.
- Hajítás: függőleges: egyszerű gyorsulási feladat, a gyorsulás nagysága g. vízszintes és általános: mindig felbontható a mozgás egy egyenes vonalú egyenletes mozgást és egy szabadesést leíró komponensre. A test pillanatnyi állapota ezek szuperpozíciójával írható le.
- Körmozgás: kényszerfeltétel: a test egy rögzített, r sugarú pályán, egy adott (rögzített) középpont körül mozoghat. Főbb mennyiségek:
- Periódusidő: egy körülfordulás ideje, jele: T, mértékegysége: másodperc. (Fordulatszám = 1/T).
- Szögelfordulás: adott idő alatt a kiindulási helyzetből történő elfordulás szöge. Jele:
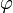 , vagy
, vagy 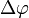 (ha két időpont közötti szögváltozást nézzük).
(ha két időpont közötti szögváltozást nézzük). - Ívhossz: adott idő alatt befutott pályaszakasz (ívhossz, mert ez a kör kerületének törtrésze), jele:
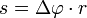 .
. - Sebesség: időegység alatt befutott ívhossz:
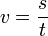 .
. - Szögsebesség: egységnyi idő alatti szögelfordulást adja meg; jele:
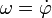 .
. - A sebesség és a szögsebesség közötti kapcsolat:
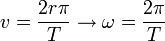 .
. - A fentiek alapján a körmozgás sebessége, a kerületi sedbesség:
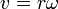
A körmozgást végző test sebességének iránya pillanatról pillanatra, változik, ezért a körmozgást végző test gyorsul. A gyorsulás értéke:
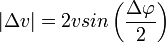 . Kis szögekre azonban:
. Kis szögekre azonban: 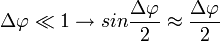 . Ennek alapján a fenti kifejezést a következőképpen írhatjuk át:
. Ennek alapján a fenti kifejezést a következőképpen írhatjuk át:
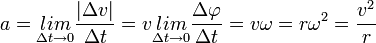 . A gyorsulás iránya megegyezik a sebességváltozás irányával, ami
. A gyorsulás iránya megegyezik a sebességváltozás irányával, ami 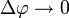 határesetben merőleges a sebbességre, és a kör középpontja felé mutat. Ezért az egyenletes körmozgást végző test gyorsulását centripetális gyorsulásnak nevezzük., amelyet a fentebbi kifejezéssel adhatunk meg. Vektoros alakban pedig:
határesetben merőleges a sebbességre, és a kör középpontja felé mutat. Ezért az egyenletes körmozgást végző test gyorsulását centripetális gyorsulásnak nevezzük., amelyet a fentebbi kifejezéssel adhatunk meg. Vektoros alakban pedig:
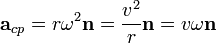 , ahol n a kör középpontja felé mutató (normális) egységvektor.
, ahol n a kör középpontja felé mutató (normális) egységvektor.
Egyenletesen gyorsuló körmozgás esetén mind az ívhossz, mint a szögelfordulás az idő négyzetével arányos, és bevezetjük a szöggyorsulást, amely a szögsebesség idő szerinti első deriváltja: 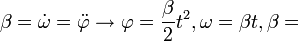 állandó.
állandó.
Szögsebességvektor: vegyünk egy Q pontot a körmozgás síkjára merőlegesen, amiből kiinduló, a körmozgás rögzített pontja felé irányuló egységvektor és a szögsebesség értékének szorzata a szögsebességvektor. Válasszunk egy r vektort, mely a Q pontból a test aktuális helyére mutat, és a rendszert úgy alakítsuk ki, hogy (e,r,v) jobbsodrású rendszer legyen. Ekkor a pillanatnyi sebesség: 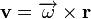
A harmonikus rezgések a körmozgás adott egyenesre levetített változatai.
Mozgás leírása különböző koordinátarendszerekben
Kiindulási alapként a Descartes-koordinátákat használom (DK - x, y, z), ehhez írom fel a különböző egyéb koordinátarendszerekre történő átszámítást oda és vissza.
| Hengerkoordináták (HK) | Gömbi koordináták (GK) |
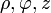 |
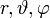
|
DK  HK HK |
DK  GK GK
|
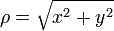 |
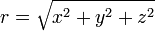
|
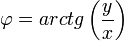 |
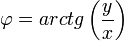
|
 |
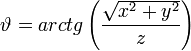
|
DK  HK HK |
DK  GK GK
|
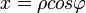 |
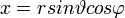
|
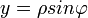 |
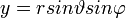
|
 |
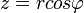
|
A sebességek/gyorsulások kiszámítása a Descartes-koordináták alapján történik, csak x, y, z helyére mindig a másik koordinátarendszerbeli megfelelőjét kell behelyettesíteni (természetesen a deriválási szabályok figyelembevételével).
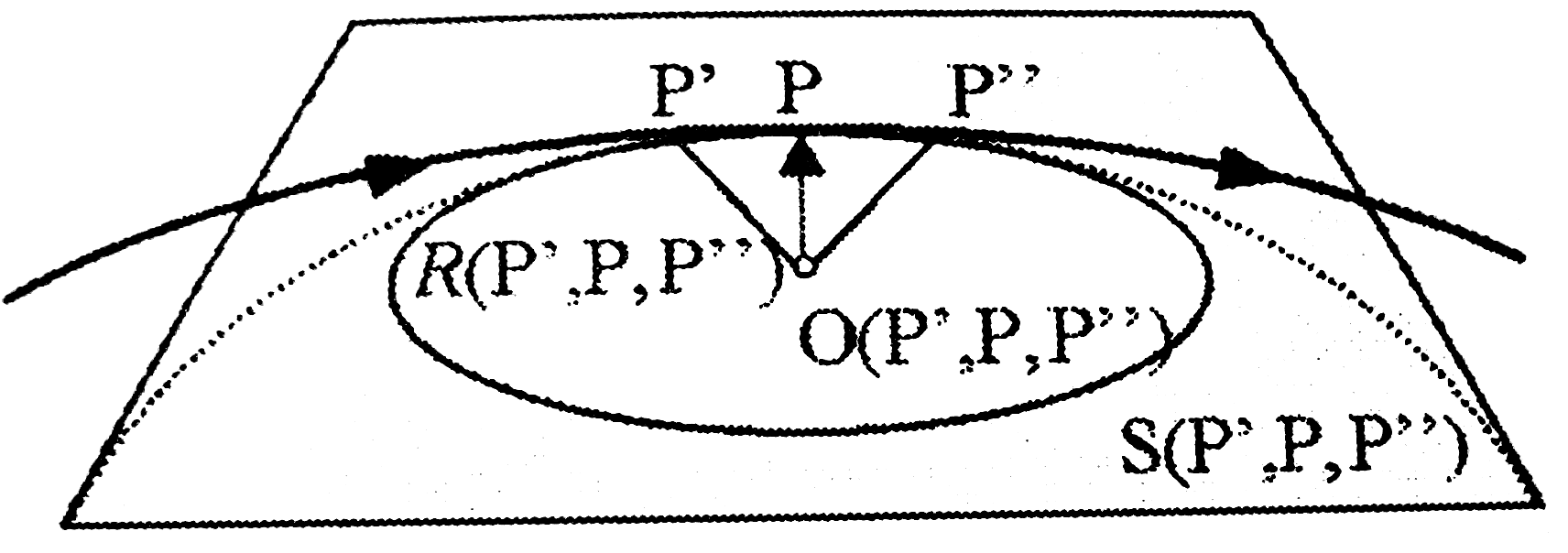
Simulósík és simulókör
Legyen egy mozgó pont t időpillanatban a pályagörbe P pontjában. Ehhez felvesszük egy kis idővel korábbi, majd egy kis idővel későbbi (P'(t') és P''(t'')) pontokat. A P', P, P'' ponthármas egy síkot határoz meg, illetve ezen a három ponton keresztük kör rajzolható, melynek középpontja a P'P és a P''P szakaszok felezőmerőlegeseinek metszéspontja. Ha t' t és t''
t és t'' t, akkor a fent nevezett síkot simulósíknak, a kört simulókörnek nevezzük, melynek sugara R(P). A térgörbe P pontbeli görbületét a
t, akkor a fent nevezett síkot simulósíknak, a kört simulókörnek nevezzük, melynek sugara R(P). A térgörbe P pontbeli görbületét a 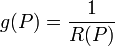 . Kis sugárhoz nagy görbület tartozik, az egyenes görbülete minden pontban nulla. A síkgörbe görbületi sugara egyébként minden olyan pontban, ahol
. Kis sugárhoz nagy görbület tartozik, az egyenes görbülete minden pontban nulla. A síkgörbe görbületi sugara egyébként minden olyan pontban, ahol 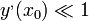 , ott körülbelül:
, ott körülbelül: 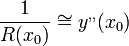
A természetes koordinátarendszer
A térgörbe a P pont környezetében belesimul a simulósíkba. A görbe adott pontbeli t érintő egységvektora a simulókör középpontja felé mutató n egységvektorra merőleges. A fenti két vektor a simulósíkban van. Erre a síkra válasszunk egy merőleges egységvektort, amely a P pontból indul ki, méghozzá úgy, hogy a (t, n, b) jobbsodrású, derékszögű rendszer legyen. A (t, n, b) koordinátarendszert természetes koordinátarendszernek nevezzük. Sebesség: 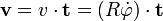 , gyorsulás:
, gyorsulás: 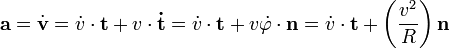
Speciális térbeli mozgások
| Csavarmozgás | Ciklois mozgás | Spirál | Logaritmikus spirál |
 |
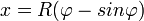 |
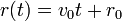 |
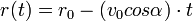
|
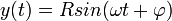 |
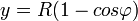 |
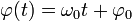 |
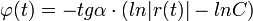
|
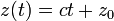 |
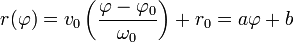 |
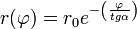
|
A sebességek kiszámítása itt is az idő szerinti első deriváltakkal történik.
Newton törvények, statika, dinamika, erőfogalom, mozgásegyenlet, tehetetlen és súlyos tömeg, Eötvös-kísérlet
Statika
A statika a mechanikának az az ága, mely a különböző rendszerekre ható, vagy azokban ébredő erőket, forgatónyomatékokat/momentumokat vizsgálja statikus egyensúlyban, azaz olyan állapotban, ahol a testek egymáshoz viszonyított helyzete időben nem változik, vagy ahol a komponensek és struktúrák állandó sebességgel mozognak. Statikus egyensúlyban a rendszer nyugalomban van, vagy a tömegközéppontja egyenes vonalú egyenletes mozgást végez. A mozgó testeket a dinamika vizsgálja.
Dinamika
A különböző fizikai jelenségek időbeli fejlődését vizsgálja.
Erőfogalom
- Empirikus: Az erő bármi olyan hatás, mely egy tömeggel rendelkező testet gyorsulásra késztet. Rugós erőmérőnél a rugó azért nem gyorsul, mert benne ellenerő ébred.
- Dinamikai: Adjuk meg a mozgásállapot-változást a sebességváltozás és a tömeg segítségével. Ha két teljesen egyforma kocsit ütköztetünk, azok "sebességet cserélnek" az ütközés után. Ha különbözőeket, akkor a sebességváltozások nem lesznek egyenlőek, de megfelelő (önkényes) szorzók bevezetésével egyenlővé tehetőek:
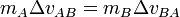 . A
. A 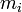 szorzók az ütköző kocsik tulajdonságát fejezik ki. Belátható, hogy három testet páronként ütköztetve a fenti egyenlet mintájára kapott három egyenletből álló túlhatározott egyenletrendszer megoldható, a testekre jellemző együtthatót találtunk. Vezessük be az impulzusváltozás (lendületváltozás) mennyiségét:
szorzók az ütköző kocsik tulajdonságát fejezik ki. Belátható, hogy három testet páronként ütköztetve a fenti egyenlet mintájára kapott három egyenletből álló túlhatározott egyenletrendszer megoldható, a testekre jellemző együtthatót találtunk. Vezessük be az impulzusváltozás (lendületváltozás) mennyiségét: 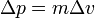 , ahol m a fentebb megismert szorzó, a test tömege. A kocsikat különböző minőségű rugós erőmérőkkel ellátva tapasztalható, hogy ugyanaz a mozgásállapot-változás különböző idő alatt is végbemehet, a mechanikai kölcsönhatás folyamatának elemzésére szolgáló erőt ezért célszerű az
, ahol m a fentebb megismert szorzó, a test tömege. A kocsikat különböző minőségű rugós erőmérőkkel ellátva tapasztalható, hogy ugyanaz a mozgásállapot-változás különböző idő alatt is végbemehet, a mechanikai kölcsönhatás folyamatának elemzésére szolgáló erőt ezért célszerű az 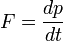 alak felírása (ezt az összefüggést impulzustételnek is nevezik).
alak felírása (ezt az összefüggést impulzustételnek is nevezik).
Newton törvények, tehetetlen tömeg
- Tehetetlenség törvénye: erőhatás mentes inerciarendszerben minden test nyugalomban van, vagy egyenes vonalú egyenletes mozgást végez.
- Mozgás törvény (dinamika alaptörvénye): különböző erők, különböző gyorsulásokat hoznak létre a testeken, de az arány jellemző a testre, ez a tehetetlen tömeg.
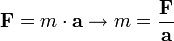 .
. - Hatás-ellenhatás törvénye: Ugyanakkora, de ellentétes irányú erő ébred minden párkölcsönhatásban.
- Erőhatások függetlenségének elve (szuperpozíció): A test úgy mozog, mint a ráható erők által egyenként létrehozott mozgások eredője.
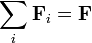
Mozgásegyenlet
A dinamika alaptörvénye a testre ható eredő erő és a test gyorsulása között állapít meg kapcsolatot. A törvény segítségével, ha az erőket ismerjük, akkor a test mozgására következtethetünk, ha a test kinematikai jellemzőit ismerjük, akkor az erőkről nyerhetünk információkat. A tapasztalat azt mutatja, hogy az erők igen sokszor a kölcsönhatás természetétől függetlenül, pusztán az erőt kifejtő test meghatározott paramétereinek (pl. a helykoordinátáinak) függvényében megadhatók. Az ilyen függvényeket erőtörvényeknek nevezzük. Azt az egyenletet, amit akkor kapunk, ha a dinamika alaptörvényébe beírjuk az erőtörvényeket, valamint a gyorsulás helyébe a helyvektor második deriváltját, mozgásegyenletnek nevezzük.
Az 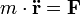 mozgásegyenlet általában a mozgás pályáját meghatározó másodrendű differenciálegyenlet. Ahhoz, hogy a mozgás pontos leírását megadjuk, az erők mellett valamely pillanatban ismernünk kell a mozgás kinematikai jellemzőit is (vagyis a kezdőfeltételeket).
mozgásegyenlet általában a mozgás pályáját meghatározó másodrendű differenciálegyenlet. Ahhoz, hogy a mozgás pontos leírását megadjuk, az erők mellett valamely pillanatban ismernünk kell a mozgás kinematikai jellemzőit is (vagyis a kezdőfeltételeket).
Tehetetlen és súlyos tömeg
Newton második törvényében - mint fentebb látható - a tömeg, mint a tehetetlenség mértéke jelenik meg. A tehetetlen tömeg számértéke alapján a testek sorrendbe rakható aszerint, hogy mennyire gyorsulnak az adott erő hatására.
Newton gravitációs törvényében azonban a testeknek az a tulajdonsága nyilvánul meg, hogy mennyire vonzzák egymást. Ez egészen távolinak tűnhet a tehetetlen tömeg fogalmától, megkülönböztetésül nevezzük el súlyos tömegnek, és helyettesítsünk be a mozgásegyenletbe:
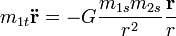
A fenti mozgásegyenletben az egyes test mindkét tulajdonsága szerepel. A kérdés az, hogy a súlyos, és a tehetetlen tömeg egyenlő-e, egyszerűsíthetünk-e 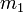 -gyel? Newton fonalinga-kísérletekben vizsgálta ezt a kérdést, ahol adott fonalhosszúság mellett változtatta a lengő test anyagi minőségét és mérte a periódusidőt.
-gyel? Newton fonalinga-kísérletekben vizsgálta ezt a kérdést, ahol adott fonalhosszúság mellett változtatta a lengő test anyagi minőségét és mérte a periódusidőt. 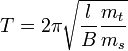 , ahol B a Föld sugarára és tömegére jellemző állandó, l a fonal hossza,
, ahol B a Föld sugarára és tömegére jellemző állandó, l a fonal hossza, 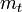 és
és 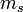 pedig a súlyos és tehetetlen tömeg. Ha a kettő eltérő lenne, akkor az anyagi minőségtől függően változna az inga lengésideje. Newton mérési pontosságon belül ilyet nem tapasztalt, azaz a tehetetlen és a súlyos tömeg aránya állandó, az anyagi minőségtől függetlenül. A súlyos és tehetetlen tömeg arányát igen nagy pontossággal Eötvös Loránd mérte.
pedig a súlyos és tehetetlen tömeg. Ha a kettő eltérő lenne, akkor az anyagi minőségtől függően változna az inga lengésideje. Newton mérési pontosságon belül ilyet nem tapasztalt, azaz a tehetetlen és a súlyos tömeg aránya állandó, az anyagi minőségtől függetlenül. A súlyos és tehetetlen tömeg arányát igen nagy pontossággal Eötvös Loránd mérte.
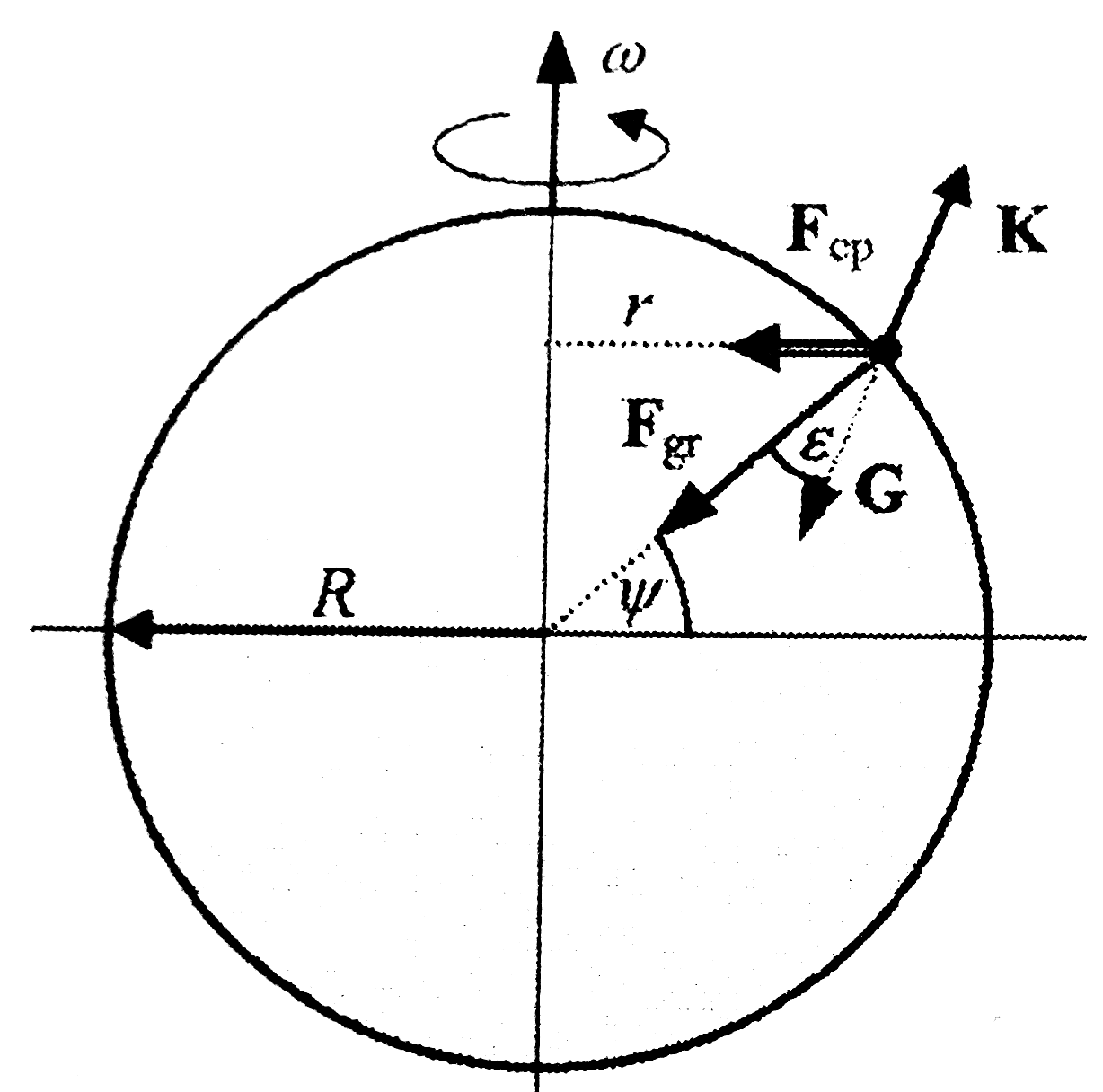
Eötvös-kísérlet
Eötvös az 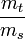 arányt az általa kifejlesztett torziós ingával mérte (1889-ben). A mérés a következő elven alapult: a forgó Földhöz képest nyugvó testre - inerciarendszerből szemlélve - hat a Föld gravitációs vonzásából származó
arányt az általa kifejlesztett torziós ingával mérte (1889-ben). A mérés a következő elven alapult: a forgó Földhöz képest nyugvó testre - inerciarendszerből szemlélve - hat a Föld gravitációs vonzásából származó 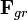 erő, valamint a talaj által kifejtett K kényszererő. A két erő tartja körpályán a testet:
erő, valamint a talaj által kifejtett K kényszererő. A két erő tartja körpályán a testet: 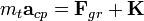 ,
,
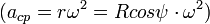 .
.
A test G súlyvektora a Föld középpontjából húzott sugárral  szöget zár be. Ez a szög megadható az
szöget zár be. Ez a szög megadható az 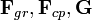 vektorokból álló háromszögre:
vektorokból álló háromszögre:
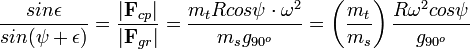 A fenti egyenlet teremt kapcsolatot a súlyos és a tehetetlen tömeg között. A
A fenti egyenlet teremt kapcsolatot a súlyos és a tehetetlen tömeg között. A 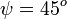 földrajzi szélességen a súlyos és a tehetetlen tömeg megegyezősége esetén
földrajzi szélességen a súlyos és a tehetetlen tömeg megegyezősége esetén 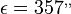 . Ha
. Ha  adott helyen, különböző testekre más és más lenne, az azt jelenteni, hogy a súlyos és tehetetlen tömeg aránya anyagi minőségtől függ.
adott helyen, különböző testekre más és más lenne, az azt jelenteni, hogy a súlyos és tehetetlen tömeg aránya anyagi minőségtől függ.
Eötvös módszere a következő volt: A torziós inga vízszintes rúdjára azonos magasságban függesztett testeket. A rúd egyik végére platina hengert, a másik végére pedig különböző anyagú testeket. Ha a két test súlyának iránya különbözik, akkor a torziós szál kissé elcsavarodik. Ha az inga rúdját K-Ny irányba állítva egyensúlyba állítjuk, akkor nem lehet megállapítani, hogy a torziós szál csavarodásmentes állapotában hol lenne az ingarúd egyensúlyi helyzete. amennyiban azonban az egész ingatestet, a torziószálat tartalmazó műszerházzal és a felfüggesztéssel együtt száznyolcvan fokkal elforgatjuk, akkor az első helyzetben ható forgatónyomaték ellentétes irányúvá válik, emiatt az ingarúdnak az első mérési helyzethez képest el kellett volna fordulnia. Ilyet azonban Eötvös nem tapasztalt, pedig a 357" milliomod részét is képes volt kimutatni a műszere. A tehetetlen és súlyos tömeg közötti eltérés Eötvös méréseiben: 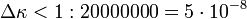 .
.
Gyorsuló koordinátarendszerek, tehetetlenségi erők
Ha egy egyenes vonalon egyenletesen gyorsuló koordinátarendszerben végzünk kísérleteket, akkor azt tapasztaljuk, hogy:
- A magára hagyott test gyorsul,
- A nyugalom fenntartásához erő kell.
Ezek alapján a Newton-törvények nem tarthatóak fenn eredeti alakukban. Ez azt jelenti, hogy a gyorsuló rendszer nem inerciarendszer. Ebben az esetben a számítások úgy végezhetőek el, ha bevezetünk egy fiktív erőt, amely a mozgástörvényben a ható erőkből vonódik le, és értéke a koordinátarendszer gyorsulása szorozva a tekintett test tömegével:
a' ekkor a relatív gyorsulás.
Ha a koordinátarendszerünk forgó mozgást végez, akkor az szintén nem lesz inerciarendszer. Belátható, hogy ekkor tetszőleges V vektor nyugalmi rendszerben vett időderiváltjára és a forgórendszerben vett deriváltjára a következő kapcsolat áll fennt:
Ezt alkalmazva a helyvektorra kétszer, megkapjuk a gyorsulásokat és a tömeggel beszorozva a fiktív erőket. A kifejezés ekkor:
Az első korrekciós tag az egyenes gyorsulásnál is fellépett transzlációs tag, a második a centrifugális erő, a harmadik a Coriolis-erő, a negyedik az Euler-erő.
Jelenségek a forgó Földön
A fentiek egy életszerű alkalmazása a forgó Földön megfigyelhető jelenségek számolása. A Föld gyakorlatilag egyenletesen forog, így az Euler-erő nem lép fel. A centrifugális erő a kettős keresztszorzat hatására a forgási tengelytől kifelé mutat. Ennek hatására a nehézségi erő csökken, továbbá irányát is megváltoztatja egy kicsit. A centrifugális erő hatása a Föld lapultsága is. Igen kis mértékben a nehézségi erő vektora érzékeny a közelében levő anyagsűrűség eloszlására. Ezt igen érzékeny műszerekkel, például az Eötvös-ingával ki lehet mérni, ennek segítségével próbáltak több helyen az országban kőolajat keresni.
Mozgó testek esetén játszik szerepet a Coriolis-erő. Célszerű lehet a szögsebességet a lokális felszínre merőleges és érintőleges komponense bontani. Ekkor a Coriolis-erőnek három tagja lesz amelyek három rokon jelenségért felelősek:
- A vízszintesen elindított test az északi féltekén jobbra, délen balra térül el,
- A lefelé mozgó testek keletfelé, a felfelé mozgó testek nyugatra térülnek el,
- A kelet felé mozgó testekre az erő függőlegesen felfelé hat, a nyugatfelé mozgókra lefelé.
A második pont igen nagy jelentőségű a mérsékeltövi ciklonok leírásában, amelyek mozgására igen nagy hatással van a Coriolis-erő.
Foucault-kísérlet
Szintén az előbbiekhez tartozik a Jean Foucaoult által demonstrált kísérlet, amelyben egy felfüggesztett és lengésbe hozott inga lengéssíkja lassan elfordul, ahogy a lengés vízszintes sebessége miatt a fenti első pontban leírt erő hat rá.
Munka tétel
Definiáljuk F erő munkáját úgy, mint az erő és az erő irányába eső elmozdulás szorzatát: 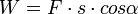 , ha F erő
, ha F erő 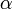 szöget zár be az elmozdulás irányával. Az erő azonban helyről helyre változhat, vezessük be az elemi munkát, amelyen olyan kis szakaszokon nézzük az erőt, ahol az állandónak tekinthető. Az elemi munka definíciója:
szöget zár be az elmozdulás irányával. Az erő azonban helyről helyre változhat, vezessük be az elemi munkát, amelyen olyan kis szakaszokon nézzük az erőt, ahol az állandónak tekinthető. Az elemi munka definíciója: 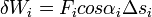 .[3]
A teljes munka ekkor:
.[3]
A teljes munka ekkor: 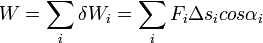
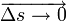
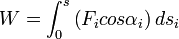
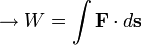 (ahol F és s vektorok).
(ahol F és s vektorok).
Eddig egyenes pályával és változó erővel foglalkoztunk, most nézzük a teljesen általános, görbe vonalú pályát (g). Ezen felvehetünk tetszőlegesen kicsiny ívdarabokat, amelyeket az ívdarab kezdőpontjából a végpontjába mutató elmozdulásvektorral helyettesítünk. Az ívdarabok hosszával a nullához tartva a következőt kapjuk (egyébként az F erő (g) görbe mentén vett vonalintegrálját): 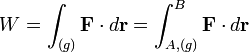 . A munka skalármennyiség, értéke pozitív és negatív is lehet. Dimenziója:
. A munka skalármennyiség, értéke pozitív és negatív is lehet. Dimenziója: 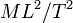 , mértékegysége:
, mértékegysége: 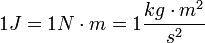
A munkatétel leírásához induljunk ki az impulzustételből: 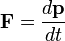 , és szorozzuk meg az egyenletet a pálya kicsiny szakaszát megadó
, és szorozzuk meg az egyenletet a pálya kicsiny szakaszát megadó 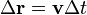 elemi elmozdulással. Ekkor az elemi munka:
elemi elmozdulással. Ekkor az elemi munka:
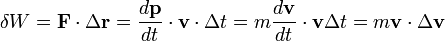 , mivel
, mivel 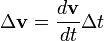 .
.
És használjuk fel azt is, hogy: 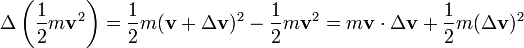 , amiből elemi sebességmegváltozás esetére az következik, hogy:
, amiből elemi sebességmegváltozás esetére az következik, hogy: 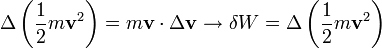 . Az elemi munkára adódó járulékokat a teljes pályára összeadva a következőt kapjuk:
. Az elemi munkára adódó járulékokat a teljes pályára összeadva a következőt kapjuk: 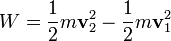 , ahol
, ahol 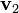 és
és 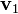 rendre a test sebessége a pálya végpontjában és kezdőpontjában. Ez a munkatétel.
rendre a test sebessége a pálya végpontjában és kezdőpontjában. Ez a munkatétel.
Az 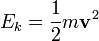 mennyiséget kinetikus, vagy mozgási energiának nevezzük.
mennyiséget kinetikus, vagy mozgási energiának nevezzük.
Impulzus-tétel
Pontosabb megfogalmazása Newton második törvényének: 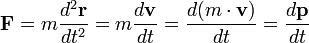 , azaz az erő az impulzus - lendület - idő szerinti első deriváltja. Ezt az összefüggést impulzustételnek nevezik.
, azaz az erő az impulzus - lendület - idő szerinti első deriváltja. Ezt az összefüggést impulzustételnek nevezik.
Impulzusmomentum-tétel
Írjuk fel a dinamika alaptörvényét pontszerű testre és szorozzuk balról vektoriálisan a test helyvektorával:
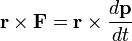 . Az egyenlet jobb oldalát alakítsuk át a differenciálási szabályok figyelembe vételével a következőképpen:
. Az egyenlet jobb oldalát alakítsuk át a differenciálási szabályok figyelembe vételével a következőképpen: 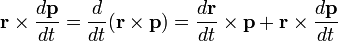 . Mivel r idő szerinti első deriváltja, azaz a sebességvektor párhuzamos p impulzusvektorral, ezért a vektoriális szorzatuk nulla, a jobb oldal első tagja ezért zérus.
. Mivel r idő szerinti első deriváltja, azaz a sebességvektor párhuzamos p impulzusvektorral, ezért a vektoriális szorzatuk nulla, a jobb oldal első tagja ezért zérus.
Vezessük be az impulzusnyomatékot (perdületet): 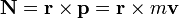 . Ami a forgatónyomatékkal a következő kapcsolatban áll:
. Ami a forgatónyomatékkal a következő kapcsolatban áll: 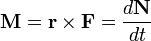 .
.
A dinamika alaptörvényének közvetlen következményeként kapott összefüggés azt fejezi ki, hogy a pontszerű testre ható erők forgatónyomatékainak eredője megegyezik a test impulzusnyomatékának időderiváltjával. Ezt az összefüggést nevezik impulzusmomentum-tételnek, vagy más néven perdülettételnek.
Pontrendszerek
Pontrendszerről akkor beszélünk, ha tömegpontoknak olyan halmazát tekintjük, amelyek között csak centrális erők hatnak. A tömegponok közötti erőket belső erőknek, a környezetből eredő erőhatásokat külső erőknek nevezzük.
Pontrendszerek tételei
Az egyes tömegpontok mozgásegyenleteinek összegzéséből kapható a következő összefüggés:
A hatás-ellenhatás törvénye miatt a belső erők teljes szummája zérus.
Impulzus-tétel
A fenti szummából egy időderiváltat kiemelhetünk:
Az időderiválás mögött a pontrendszer teljes impulzusa áll, ez a pontrendszer impulzus-tétele.
Tömegközéppont-tétele
Egy pontrendszer mozgása jellemezhető dinamikai szempontból egyetlen pont mozgásával, amely pontban egyesül a pontrendszer összimpulzusa. Másképp megfogalmazva, bármely pontrendszer tömegközéppontja úgy mozog, mintha benne a rendszer össztömege lenne egyesítve, és rá a rendszerre ható erők eredője hatna. Ennek a pontnak a helyvektora:
Impulzusmomentum-tétel
Ha az N darab tömegpont mozgásegyenleteit vektoriálisan megszorozzuk a helyvektorral, és összeadjuk őket, akkor a belső erők forgatónyomatékai megfelelő felbontások után kiejtik egymást, hasonlóan az impulzustételben látottakhoz. A végeredményben az időderiváláts hasonlóan kiemelve:
Baloldalon a rendszerre ható erők eredő forgatónyomatéka áll, jobboldalon a deriválás alatt pedig a rendszer összeimpulzusnyomatéka (perdülete). Ez a pontrendszerre vonatkozó impulzusmomentum-tétel.
Az impulzusmomentum felbontható egy saját- és egy pályaösszetevőre. A pályaösszetevő időbeli megváltozása a tömegközéppontra ható külső erők forgatónyomatéka. A sajátösszetevőre a változás a tömegközépponti rendszerben felírt helyvektorokkal felírt forgatónyomatékok összege a külső erők hatására.
Munka-tétel
A mozgásegyenleteket most kis elmozdulásokkal beszorozva az erők által végzett munkák összegét kaphatjuk meg. Itt nem esnek ki az erők, ezért az eredményben is megmarad a külső erők összmunkája, és a belső erők összmunkája. A kettő összege egyenlő a kinetikus energia megváltozásával:
Az energiakifejezés átírható a tömegközéppont mozgásából származó járulék és az akörüli mozgásból származó járulék összegáre:
ahol 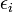 -k a tömegközépponthoz viszonyított sebességek.
-k a tömegközépponthoz viszonyított sebességek.
Merev testek
Merevnek nevezzük azt a testet, amelyre tetszőleges kölcsönhatás során fennáll, hogy közben bármely két pontjának távolsága állandó. Matematikai alakban ezt a következőképpen fejezhetjük ki: legyen a merev test tetszőleges két pontjának valamely O vonatkoztatási pontból húzott helyvektora r_A és r_B (A és B pontba mutatnak). Ekkor a két pont közötti
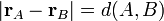
távolság állandó. A merev test helyzetét három, nem kollineáris pontjának koordinátáival jellemezhetjük. A test egy A pontjának rögzítése után a merev test pontjai a rögzített pont körüli gömbfelületen mozoghatnak. Ha a testnek egy másik, B pontját is rögzítjük, akkor a test az A és B ponton átmenő tengely körül még elfordulhat. A tengely egyenesén kívül fekvő, egyébként tetszőleges harmadik, C pontjának rögzítésével már az egész test helyzete megadható. A három pont helyének megadásához kilenc koordináta szükséges. A merev kötés miatt azonban ezek között három összefüggést írhatunk fel; például azt, hogy a három pont közül bármely kettőnek a távolsága állandó. Mivel a kilenc adat közül három nem független, a merev test helyzete általában 6 független adattal jellemezhető. Ezt úgy mondjuk, hogy a szabad merev testnek 6 szabadsági foka van (ebből három egy tetszőleges pont x,y,z koordinátája, a másik három pedig az Euler-szögek).
Sztatika: az egyensúly feltétele
Ha egy szabad merev test mozgását le akarjuk írni, két út áll rendelkezésre. Az egyik az, hogy bevezetjük a merev test helyzetét jellemző 6 független koordinátáit, és ezekben, mint általános koordinátákban a Lagrange-féle egyenleteket felírjuk; a másik pedig az, hogy kiindulunk a bármely pontrendszerre érvényes tömegközéppont-tételből és impulzusmomentum-tételből:
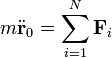 [1]
[1]
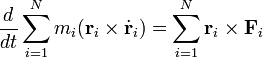 [2]
[2]
Egy anyagi pontnál az egyensúly szükséges és elégséges feltétele, hogy a pontra ható összes erők eredője zérust adjon. Merev testnél az ennek megfelelő feltétel nem elegendő, mert [1] szerint csak a tömegközéppont gyorsulásának hiányát jelenti, így a körülötte történő forgó mozgások lehetségesek (pl. erőpár). Tehát a forgómozgás akkor nem lép fel, ha az erők forgatónyomatékának eredője is zérus. Az összes egyensúlyi feltételt megkaphatjuk a virtuális munka elvéből:
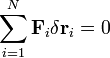
Ez a d’Alembert elv speciális esete 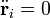 . Így szabad merev testre az alábbi feltételek adódnak:
. Így szabad merev testre az alábbi feltételek adódnak:
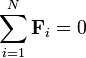 és
és 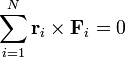
Egy nem szabad merev testnél ugyanezek a feltételek érvényesek, ha a külső erőkbe beleértjük azokat a külső kényszererőket is, amelyek a kényszerfeltételekből – az adot testnek más testekkel való érintkezéséből- származnak. Tehát: Merev test egyensúlyának szükséges és elégséges feltétele, hogy a testre ható összes külső erők eredője és a külső erők (tetszőleges pontra vonatkozó) forgatónyomatékainak eredője zérus legyen.
Az egyensúly típusai
Az egyensúly típusai alatt az egyensúlyi helyzet stabilitását értjük. Ez úgy vizsgálható, hogy a testet kissé kimozdítjuk egyensúlyából és magára hagyjuk. Ha a test a kitérítés után eredeti helyzetének környezetében marad (esetleg visszatér kiinduló helyzetébe), akkor az egyensúly stabilis. Ha a test a kimozdítás után eltávolodik az egyensúlyi helyzetéből, és nem tér oda vissza, az egyensúlyi helyzet labilis. Abban az esetben, amikor a test az új helyzetben is egyensúlyban marad, indifferens egyensúlyról van szó.
Dinamika: forgások
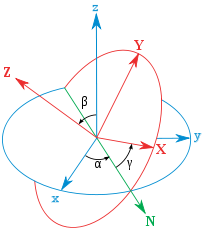
A merev testek forgásának vizsgálatához két koordinátarendszert veszünk fel: az ábrán pirossal jelölt koordinátatengelyeket tartalmazó K’-t és a kékkel megrajzolt K koordináta-rendszert. Az ábrán látható szögeket Euler-szögeknek nevezzük. Segítségükkel (és a koordinátákkal) egy merev test helyzete egyértelműen megadható a Descartes-koordinátarendszerben. Az N vonal az ún. csomóvonal, azaz az a vonal, ami a két sík metszéspontja.
Az alábbi összefoglalásban az egyes szögek mellett az általuk felvett szögintervallum látható, ill. az, hogy melyik tengely körüli helyzetváltozást írja le.
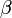 |
![[0,\pi]](/images/math/e/1/8/e1868564b62b4e2f1c063321df289469.png) |
csomóvonal |
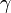 |
![[0,2\pi]](/images/math/5/8/c/58c9a5de0cb1a343ae0acd1fb191eea1.png) |
piros Z |
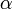 |
![[0,2\pi]](/images/math/5/8/c/58c9a5de0cb1a343ae0acd1fb191eea1.png) |
kék z |
A forgási szögsebesség pedig kifejezhető a K és K’-beli koordináták, ill. az adott tengelyek és csomóvonal irányú egységvektorok segítségével:
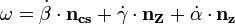
Az egységvektorok K-beli és K’-beli koordinátái pedig leolvashatóak az ábráról.
A tehetetlenségi-tenzor
Vegyünk fel egy Descartes-koordinátarendszert! Ebben a merev test tömegközéppontjának
helyvektorát jelöljük 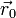 -val. Rögzítsünk a tömegközépponthoz is egy koordináta-rendszert,
amiben egy, a merev testhez tartozó tetszőleges pontnak a helykoordinátája
-val. Rögzítsünk a tömegközépponthoz is egy koordináta-rendszert,
amiben egy, a merev testhez tartozó tetszőleges pontnak a helykoordinátája 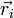 . Egy merev
test pontjának a sebessége a testre jellemző transzlációs sebességből és a forgásból
származó kerületi sebesség határozza meg
. Egy merev
test pontjának a sebessége a testre jellemző transzlációs sebességből és a forgásból
származó kerületi sebesség határozza meg 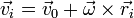
A merev test kinetikus energiája:
A második tag akkor lesz nulla, ha a testhez rögzített koordinátarendszer kezdőpontját a tömegközéppontba helyezzük, vagy ha rögzítjük a testet.
A harmadik tag felírásához először kifejtjük a vektoriális szorzatot, majd a kapott kifejezés négyzetét vesszük. Ennek eredményeképpen kapjuk az alábbi kifejezést:
ahol 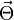 tehetetlenségi tenzor elemei:
tehetetlenségi tenzor elemei:
Másik felírási módja:
A tenzor egyes elemeit deviációs nyomatékoknak nevezzük, a főátló egyes elemei pedig a tehetetlenségi nyomaték komponensei.
Ha a testen kívüli pontból húzunk egy forgástengelyt a testen keresztül, és egy tetszőleges
pontot kiválasztunk a merev testen belül, aminek a tengelytől mért távolsága l, a ponttól vett
távolsága 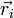 és a tengely irányú egységvektor n, akkor a test tehetetlenségi nyomatéka:
és a tengely irányú egységvektor n, akkor a test tehetetlenségi nyomatéka:
A Steiner-tétel segítségével megadhatjuk a test egy O pontján átmenő tetszőleges forgástengelyre vett tehetetlenségi nyomatékát.
ahol s a TKP és az O pont távolsága.
Merev test impulzusmomentuma:
Ahol 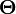 a tehetetlenségi tenzor. A forgómozgás egyenlete:
a tehetetlenségi tenzor. A forgómozgás egyenlete:
ekkor a következő alakú:
Rögzített tengely körüli forgás esetén a tengely irányába mutató egységvektorral az arra a tengelyre vontkoztatott tehetetlenségi nyomaték:
A rögzített tengely körüli forgómozgás egyenlete:
Pörgettyűk
Pörgettyűnek hívunk minden olyan merev testet, amelynek csak egy pontja (a támaszpontja) van rögzítve, vagy általánosabban, amelynek az alátámasztási pontja körüli mozgása ennek a pontnak mozgásától elkülönítve tárgyalható. A pörgettyűnek 3 szabadsági foka van. A mozgásegyenletek felírásához a pörgettyűt belehelyezzük egy forgó és egy nyugvó koordinátarendszerbe. A két koordinátarendszer origója megegyezik, a forgó rendszer nem feltétlenül forog együtt a pörgettyűvel.
Legyen 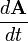 valamely A vektor változásának sebessége a nyugvó koordináta-rendszerben (K). Ha a forgó rendszerhez képest A nem változik, a nyugvó rendszerben a változás csak a forgásból áll:
valamely A vektor változásának sebessége a nyugvó koordináta-rendszerben (K). Ha a forgó rendszerhez képest A nem változik, a nyugvó rendszerben a változás csak a forgásból áll:
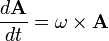
Amennyiben a pörgettyű a forgó rendszerhez képest mozgást végez, az egyenlet így módosul (K’-ben):
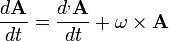
Ha A = N, akkor az egyenletünk:
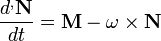
Ha K’ főtengely-rendszer: 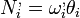 ;
; 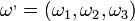
A fenti egyenletből a forgatónyomatékot kifejezve és a keresztszorzás elvégezve komponensenként megkapjuk az Euler-egyenleteket:
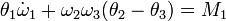
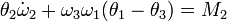
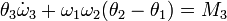
Erőmentes szimmetrikus pörgettyű
M = 0; két főtehetetlenségi nyomaték megegyezik :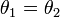 , ezek pedig nem egyeznek a harmadikkal. Így
, ezek pedig nem egyeznek a harmadikkal. Így 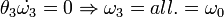 . Jó közelítéssel a Föld is ez.
. Jó közelítéssel a Föld is ez.
Ha bevezetjük az 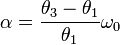 mennyiséget, és ezt, valamint az előbbi feltételeket behelyettesítjük, lineáris oszcillátort leíró eredményt kapunk:
mennyiséget, és ezt, valamint az előbbi feltételeket behelyettesítjük, lineáris oszcillátort leíró eredményt kapunk:
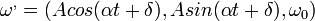
A szögsebesség az Euler-szögekkel is kifejezhetők. A felíráskor fel kell írni a szögsebesség komponenseit az Euler-szögekkel kifejezve nyugvó koordináta-rendszerben. Ezután az egyes komponenseket egyenlővé tesszük az oszcillátor rezgését leíró megfelelő komponensekkel, és a kapott egyenletrendszer megoldjuk.
Erőmentes aszimmetrikus pörgettyű
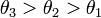
az energiamegmaradás:
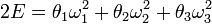 [1]
[1]
impulzusmomentum:
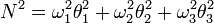 [2]
[2] 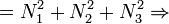 gömbfelület
gömbfelület
Az 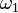 és
és 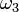 az alábbi Knorr rafinériával határozható meg:
az alábbi Knorr rafinériával határozható meg:
![\theta_1 \cdot [1] - [2] \rightarrow \omega_3^2](/images/math/f/a/3/fa34e5eb400bf901e1406231c2905169.png)
![\theta_3 \cdot [1] - [2] \rightarrow \omega_1^2](/images/math/1/9/e/19ecc3d985c27686643a708c4fe18a4a.png)
A második komponens pedig a 2. Euler-egyenletből fejezhető ki.
Szimmetrikus súlyos pörgettyű
Ennek a pörgettyűnek a mozgását csak abban az esetben vizsgáljuk, amikor a pörgettyűnek van szimmetriatengelye, a rögzített O pont ennek egyik pontja, és az S tömegközéppont is a szimmetriatengelyen van, O-tól OS=s távolságra. A térben rögzített koordinátarendszer Z tengelye mutasson függőlegesen felfelé, a testhez rögzített X’Y’Z’ fő tehetetlenségi rendszer (amelynek tengelyeire rendre az A,A,C fő tehetetlenségi nyomatékok és a p,q,r szögsebesség-komponensek vonatkoznak) helyzetét jellemezzük az Euler-szögekkel. A probléma megoldásához felhasználhatjuk a mozgásegyenletek első három integrálját (három elsőrendű differenciálegyenlet a szögekre). Az egyik integrált a T+V=const. energiatétel adja. Ha m a pörgettyű tömege, a potenciális energia (az Euler-szöges ábra! a TKP a Z’ tengelyen van):
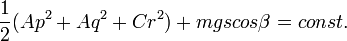
A másik két integrálhoz úgy jutunk, hogy tudjuk azt, hogy a nehézségi erő forgatónyomatéka a Z és Z’ által alkotott tengelyre merőleges, ezért a forgatónyomaték z komponense 0. Az impulzusmomentum tétele alapján 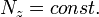 ;
; 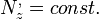
A további számítások: 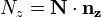 felírjuk, majd az energiatételbe p,q,r-et az Euler-szögekkel és deriváltjaival felírva behelyettesítjük. Végül megoldjuk az egyenletrendszert (a megfelelő kezdeti feltételek felírása után:
felírjuk, majd az energiatételbe p,q,r-et az Euler-szögekkel és deriváltjaival felírva behelyettesítjük. Végül megoldjuk az egyenletrendszert (a megfelelő kezdeti feltételek felírása után: 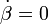 ;
; 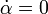 ;
; 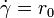 ).
).
Gyors pörgettyű
Ez a fajta pörgettyű az előbbinek egy speciális esete: ilyenkor 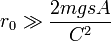 Ha a mozgást teljesen leírjuk, azt kapjuk, hogy a szimmetriatengelynek a függőlegessel bezárt szöge periodikusan ingadozik a kezdeti és egy ettől kicsit eltérő érték között. Ezt az ingadozást nutációnak nevezzük. Az ingadozások annál kisebbek, így egyúttal annál gyorsabbak, minél nagyobb a pörgettyű kezdeti
Ha a mozgást teljesen leírjuk, azt kapjuk, hogy a szimmetriatengelynek a függőlegessel bezárt szöge periodikusan ingadozik a kezdeti és egy ettől kicsit eltérő érték között. Ezt az ingadozást nutációnak nevezzük. Az ingadozások annál kisebbek, így egyúttal annál gyorsabbak, minél nagyobb a pörgettyű kezdeti  szögsebessége. A szimmetriatengely vízszintes vetülete pedig állandóan meghatározott irányban forog. A szimmetriatengely e mozgásának, a precessziónak a szögsebessége periodikusan változik 0 és egy maximális érték között. A precesszió és a nutáció együttesen az ún. pszeudoreguláris precessziót eredményezi: a szimmetriatengely végpontja az O rögzített pont köré írt gömbfelület két paralel köre között cikloisszerű görbét ír le. http://resumewriter.ws/
szögsebessége. A szimmetriatengely vízszintes vetülete pedig állandóan meghatározott irányban forog. A szimmetriatengely e mozgásának, a precessziónak a szögsebessége periodikusan változik 0 és egy maximális érték között. A precesszió és a nutáció együttesen az ún. pszeudoreguláris precessziót eredményezi: a szimmetriatengely végpontja az O rögzített pont köré írt gömbfelület két paralel köre között cikloisszerű görbét ír le. http://resumewriter.ws/
- ↑ Tasnádi-Skrapits-Bérces: Mechanika I., 4, 8, 10. §
- ↑ Tasnádi-Skrapits-Bérces: Mechanika I., 12, 17, 18, 21, 29. §
- ↑ A
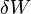 jelölés arra utal, hogy kicsiny munkavégzésről beszélünk. Mivel a munka nem a vizsgált rendszerre jellemző mennyiség, ezért a megváltozásáról nem beszélhetünk, innen a megkülönböztetés.
jelölés arra utal, hogy kicsiny munkavégzésről beszélünk. Mivel a munka nem a vizsgált rendszerre jellemző mennyiség, ezért a megváltozásáról nem beszélhetünk, innen a megkülönböztetés.
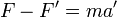
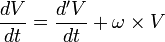
![F - ma_0 -m\left[ \omega \times \left( \omega \times R \right)\right] - 2m\left( \omega \times v^{\prime}\right) - m\left( \frac{d \omega}{dt} \times R\right) = ma^{\prime}](/images/math/f/4/c/f4cdbc4b1c2d6030d0accf0bed1c27bb.png)