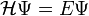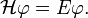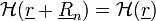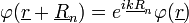Kristályos anyagok fizikája
Tartalomjegyzék
Pontcsoportok, Bravais-rácsok, szimmetriák.
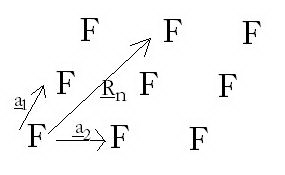
Rácsvektor (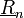 ): olyan vektor, mely mentén ha eltoljuk a rácsot, önmagába megy át. (ez a transzlációs vektor is)
): olyan vektor, mely mentén ha eltoljuk a rácsot, önmagába megy át. (ez a transzlációs vektor is)
Ez felbontható elemi rácsvektorok lineáris kombinációjára: 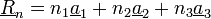
Az ilyen 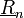 vektorral való eltolását transzlációs műveletnek nevezzük. Az ilyen műveletek összessége a transzlációs csoportot alkot.
vektorral való eltolását transzlációs műveletnek nevezzük. Az ilyen műveletek összessége a transzlációs csoportot alkot.
Pontrács: pontok olyan háló szerű elrendeződése, amelyben minden kiszemelt pont környezete minden szempontból azonos akármelyik másik pont környezetével.
Kristályszerkezetet akkor kapunk, ha a rács minden pontjában azonos összetételű irányítású atomcsoportot helyezünk el.
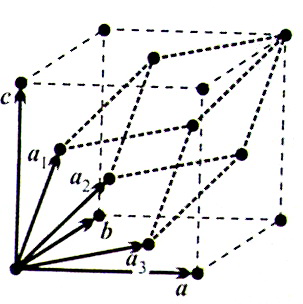
Ideális kristály: olyan test, amelynek atomjai rácsszerűen úgy helyezkednek el, hogy létezik három (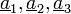 )vektor, hogy az atomi elrendeződés minden pontból ugyanolyannak látszik.
)vektor, hogy az atomi elrendeződés minden pontból ugyanolyannak látszik.
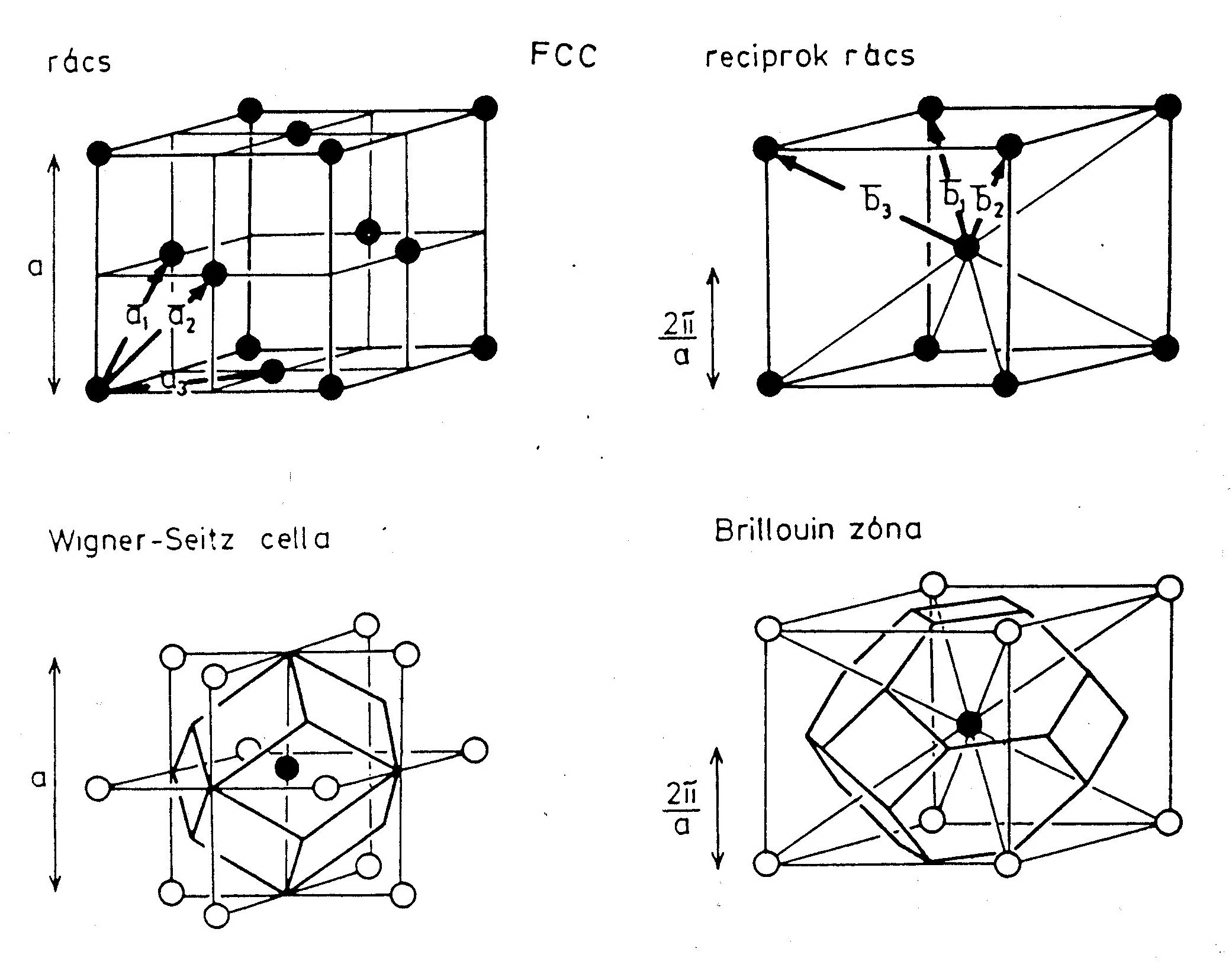
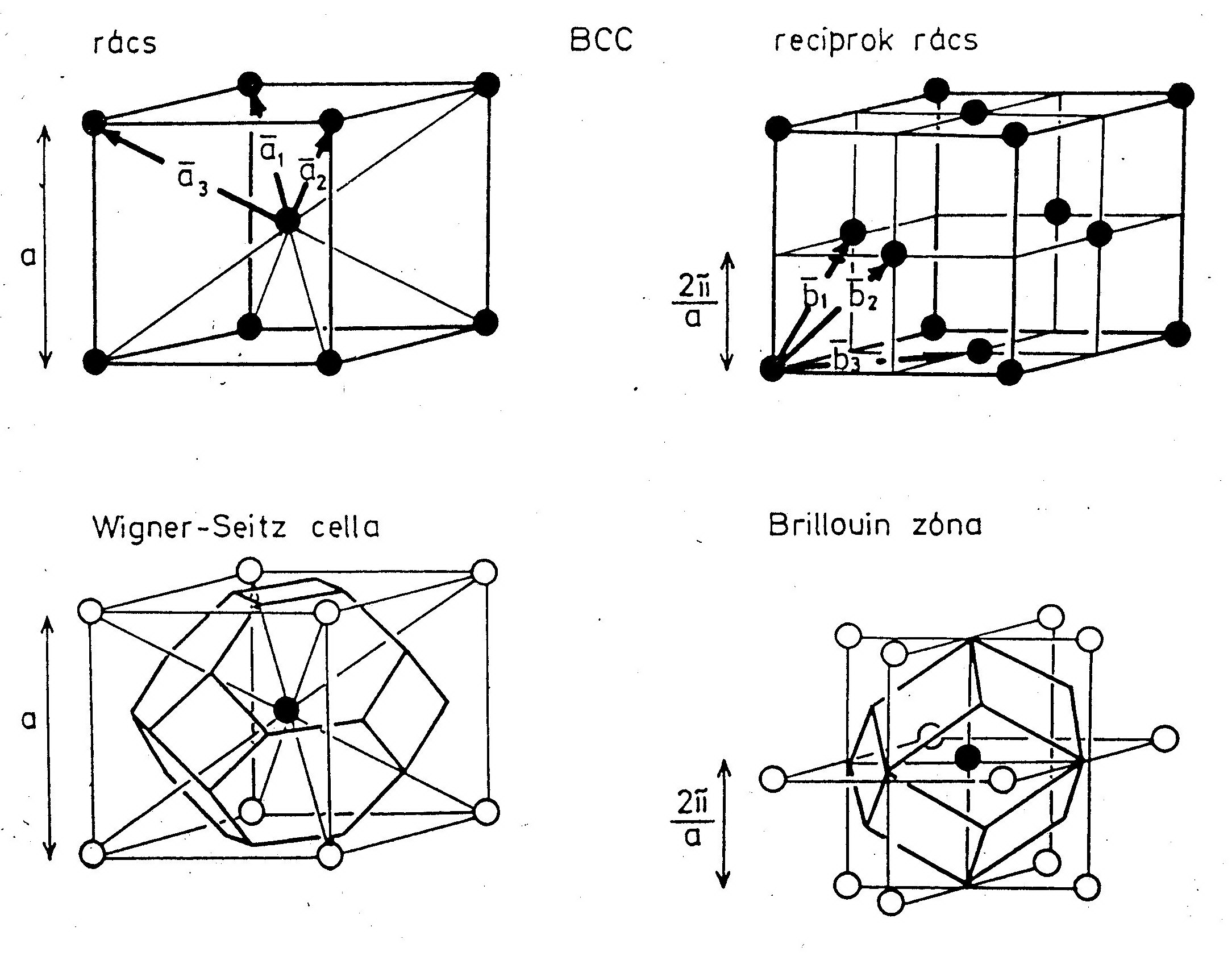
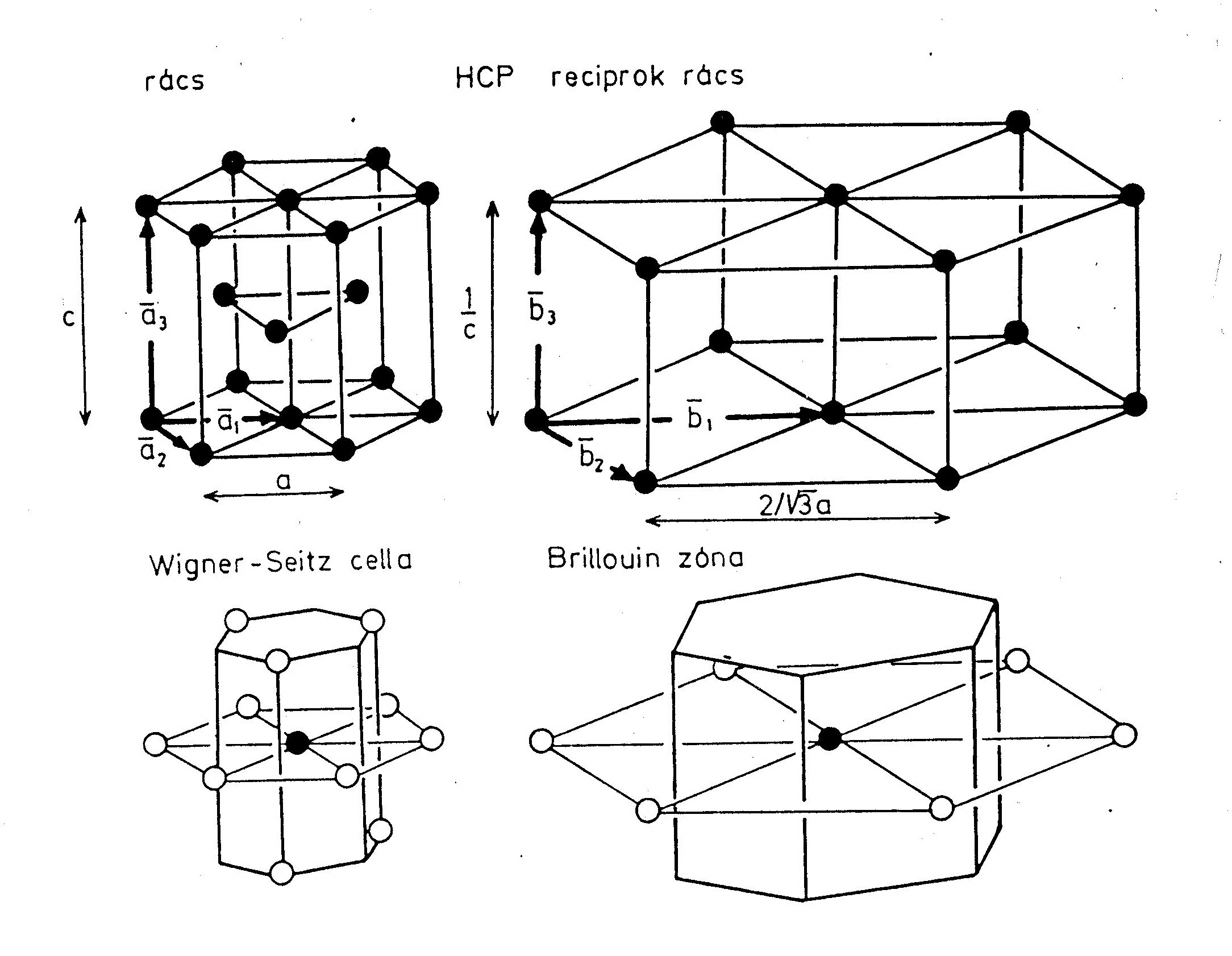
Elemi cella: elemi rácsvektorok által kifeszített paralellepipedon. 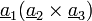 Az elemi cella primitív, ha csak a csúcsaiban tartalmaz rácspontot. Wigner-Seitz cella: Azon pontok halmaza, melyek közelebb vannak egy adott rácsponthoz, mint bármely másikhoz. (Ha a kristálynak van valamilyen szimmetriája, akkor ez a WS-cellának is megvan, míg az elemi cellának nincs!)
Az elemi cella primitív, ha csak a csúcsaiban tartalmaz rácspontot. Wigner-Seitz cella: Azon pontok halmaza, melyek közelebb vannak egy adott rácsponthoz, mint bármely másikhoz. (Ha a kristálynak van valamilyen szimmetriája, akkor ez a WS-cellának is megvan, míg az elemi cellának nincs!)
Reciprok rács: 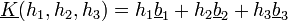 , ahol
, ahol 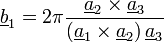
Szimmetriák
1. Transzláció: létezik az 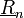 transzlációs vektor
transzlációs vektor
2. Forgatás: (inverz forgatás is megengedett)
Ha egy kiszemelt tengely körüli 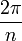 szögű forgatás egy testet önmagába visz át, akkor az ilyen tengelyt n-fogású forgástengelynek nevezik:
szögű forgatás egy testet önmagába visz át, akkor az ilyen tengelyt n-fogású forgástengelynek nevezik:
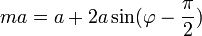
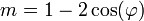
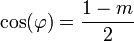
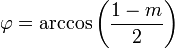
| m | -1 | 0 | 1 | 2 | 3 |
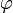
|
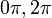
|
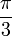
|
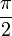
|
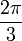
|
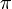
|
| n | 1 | 6 | 4 | 3 | 2 |
(kvázikristályoknál - ahol nincs periodikus szerk. - lehet 5 forgású)
3. Inverzió: (középpontos tükrözés) 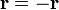
4. Csúszósík: összetett szimmetria művelet 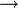 tükrözés, majd a tengely irányába való eltolás (az eltolás a fele a tengely irányába eső ismétlődési hossznak).
tükrözés, majd a tengely irányába való eltolás (az eltolás a fele a tengely irányába eső ismétlődési hossznak).
5. Tükörtengely: összetett szimmetria művelet 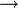 forgatás, majd inverzió:
forgatás, majd inverzió: 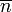 az
az 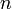 fogású tükörtengely jele,
fogású tükörtengely jele, 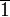 a közönséges inverzió,
a közönséges inverzió, 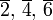 létezik.
létezik.
1-5-ig az elemi szimmetriaműveletek matematikai csoportot alkotnak, mivel ezek egymásutáni elvégzése is szimmetriaművelet (csoport szorzás művelete). A pontcsoportok a teljes ortogonális O(3) csoport diszkrét alcsoportjai, és 1-5 műveletek tetszőleges kombinációiból állnak.
Bravais-rácsok
230 tércsoport és 32 pontcsoport (7 osztályba sorolva) létezik 3D-ben, 10 pontcsoport 2D-ben
14 Bravais rács létezik 3D-ben, 7 Bravais rács létezik 2D-ben
A jelölések[1]:
• Primitív elrendezés (P): rácspontos a cellák csúcsaiban
• Tércentrált elrendezés (I): +1 rácspont a cella közepén
• Lapcentrált elrendezés (F): minden oldallap közepén +1 rácspont
• Egy oldalpáron lapcentrált (A,B vagy C): csak két (szemközti) oldal közepén van +1-1 rácspont
| A 7 kristályszimmetria | A 14 Bravais rács | |||
| Triklin | P | |||
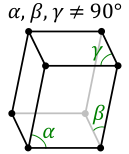
| ||||
| Monoklin | P | C | ||
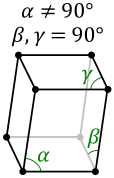
|
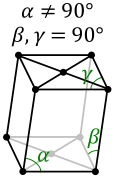
| |||
| Ortorombos | P | C | I | F |
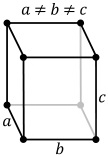
|
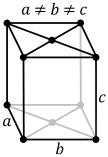
|
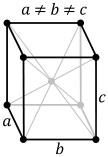
|
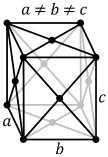
| |
| Tetragonális | P | I | ||
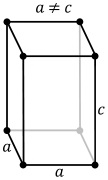
|
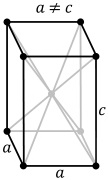
| |||
| Trigonális | P | |||
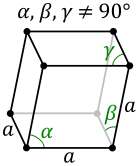
| ||||
| Hexagonális | A | |||
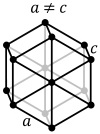
| ||||
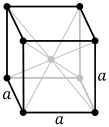
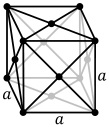
| Köbös | P (pcc) | I (bcc) | F (fcc) | |
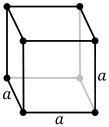
|
|
| ||
Fontosabb kristályszerkezetek[2]
1. Egyszerű köbös (SC): Po
A WS cellája is kocka.
2. Lapcentrált köbös (FCC): Cu, Al, Au, Ag, Ni, Pt ((Ez a legsűrűbb rács))
3. Tércentrált köbös (BCC): Fe, W, Mo
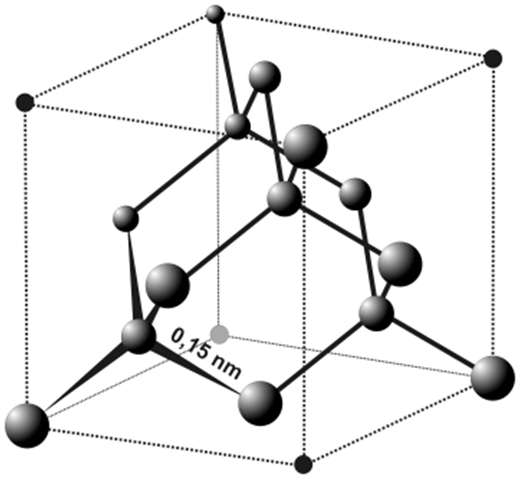
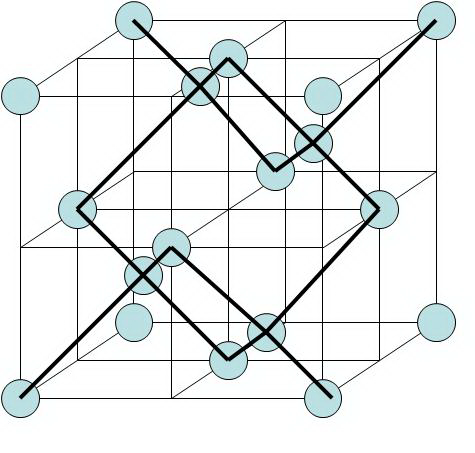
4. Gyémánt rács: 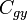 , Si, Ge
, Si, Ge
FCC rács az alapja (és minden második nyolcad kockában van atom).
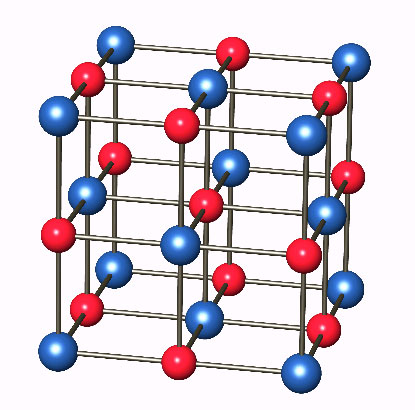
5. NaCl szerkezet: (két egymásba tolt FCC)
6. Hexagonális (szoros illeszkedésű szerkezet): Zn, Nb
4 atom tetraédert alkot. Ha szabályos ez a tetraéder, akkor teljesen szoros az illeszkedés.
Bloch tétel, adiabatikus szétcsatolás.
Adiabatikus szétcsatolás ötlete Born és Oppenheimer nyomán alakult ki, akik rámutattak, hogy az elektronokra jellemző sebesség szilárd anyagokban, a Fermi-sebesség (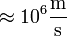 ) lényegesen nagyobb, mint a közegbeli hangsebesség (
) lényegesen nagyobb, mint a közegbeli hangsebesség (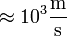 ), ami az ionok jellemző sebessége. A következtetés tehát az, hogy az ionok szemszögéből az elektronok követhetetlenül gyorsan mogoznak, az elektronok pedig úgy érzik, mintha az ionok helyben állnának. Ez igen jelentős egyszerűsítéseket tesz lehetővé, amelyeket a nem csak a szilárdtestfizika de a molekulafizika is gyakran alkalmazni tud.
), ami az ionok jellemző sebessége. A következtetés tehát az, hogy az ionok szemszögéből az elektronok követhetetlenül gyorsan mogoznak, az elektronok pedig úgy érzik, mintha az ionok helyben állnának. Ez igen jelentős egyszerűsítéseket tesz lehetővé, amelyeket a nem csak a szilárdtestfizika de a molekulafizika is gyakran alkalmazni tud.
Ionok: 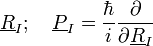
- A Hamilton-fv:
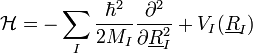
- A Hamilton-fv:
Azaz az ionokra csak a saját mozgásukat írtuk fel a saját potenciáljukban, ebben a közelítésben az elektronok hatását elhanyagoljuk.
Elektronok: 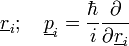
- A Hamilton-fv:
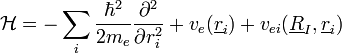
- A Hamilton-fv:
Ekkor az elektronokra szintén a saját mozgásuk és az önmaguk által keltett potenciáljuk hat, az ionok hatását egy külön kölcsönhatási potenciálban csatoljuk csak hozzájuk. Ez a két Hamilton-függvény adja együtt a rendszer Hamilton-függvényét.
Az egyensúlyi megoldás érdekében írjuk fel a sajátértékegyenletet:
A megoldást pedig keressük szorzatfüggvény alakban:
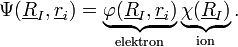
![\left[-\sum_{I}\frac{\hbar^{2}}{2M_{I}}\frac{\partial^{2}\chi}{\partial\underline{R}_{I}^{2}}+V_{I}\chi\right]\varphi+\left[-\sum_{I}\frac{\hbar^{2}}{2M_{I}}\left(2\frac{\partial\chi}{\partial\underline{R}_{I}}\frac{\partial\varphi}{\partial\underline{R}_{I}}+\chi\frac{\partial^{2}\varphi}{\partial\underline{R}_{I}^{2}}\right)\right]+](/images/math/f/c/0/fc0622408a3aad80da107b899ac50082.png)
![+\left[-\sum_{i}\frac{\hbar^{2}}{2m_{e}}\frac{\partial^{2}\varphi}{\partial r_{i}^{2}}+v_{e}\varphi+v_{ei}\varphi\right]\chi=E\chi\varphi](/images/math/9/5/3/9530ebd43c9c08d3956ef598159ee016.png)
Az első tag tehát az ionok terében az elektronok problémája (rácsprobléma), a második az elektronok-fononok kölcsönhatási problémájára vezet (Fonon: kvázirészecske, szilárd testek rezgési átmeneteinek energiakvantumai[3]). A harmadik tag az elektron probléma. Most csak az elektronproblémát, azaz az harmadik tagot tárgyaljuk. Írjuk fel (sok) elektronra az elektronproblémát, álló ionok terében:
1 elektronra: 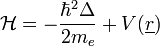
Sok elektronra: 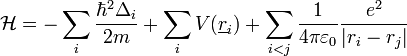
Itt az első tag az elektronok kinetikus energiája, második az ionok által keltett fix külső potenciál, a harmadik tag az elektronok saját Coulomb-potenciálja. 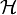 -nak invariánsnak kell lennie a rácsperiódusú eltolásra:
-nak invariánsnak kell lennie a rácsperiódusú eltolásra:
Ez akkor teljesül, ha:
Ez a Bloch-tétel, ami pedig végeredményül kijött, azt Bloch-függvénynek nevezzük. Vagyis az elektron hullámfüggvénye tükrözi a rács szimmetriáit.
A fentiek csak degenerált esetben érvényesek. Nem degenerált esetben az eltolásnál gond van a skalárszorzással, így más módszert kell alkalmaznunk (főtengelytranszformációt), de így is megkapjuk végeredményül a Bloch-függvényt.
Röntgen- és elektrondiffrakció. Diffrakció, kinetikus elmélet. Ewald-szerkesztés. Bragg-feltétel.
Röntgen-diffrakció
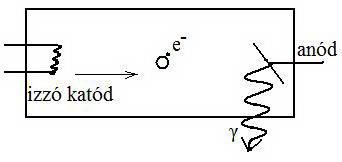
(a) Röntgencső
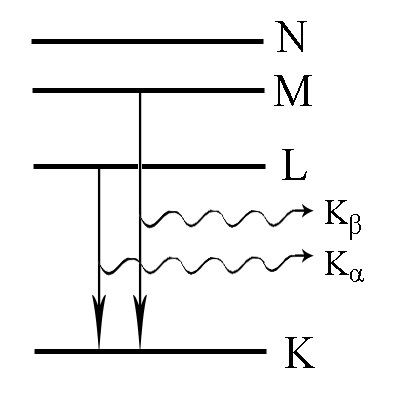
Karakterisztikus és fékezési sugárzás; Sok fékezési sugárzás, kicsi az energia.
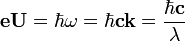
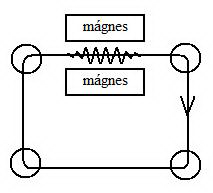
(b) Szinkrotronsugárzás
Az elektronokat fölgyorsítjuk, majd „megrázzuk” (csak fékezési sugárzás lesz)
Előnye a röntgencsőhöz képest, hogy monokróm és nagy intenzitás, de nagy a mérete és drága.
Észlelés: fotólemez, számlálócső, CCD, Imaging Plate
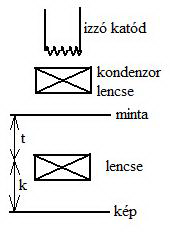
Elektronok
Elektronokkal is lehet diffrakciót létre hozni, és ezt vizsgálni (hasonló eljárássokkal, mint a röntgen-diffrakciót), viszont pontosabb és célravezetőbb, ha elektronmikroszkópot használunk anyagvizsgálatra:
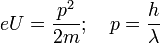
Leképezés: 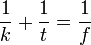 , ha k=f, akkor diffrakció van.
, ha k=f, akkor diffrakció van.
Röntgenhez képest hátrány:
- A lencserendszer miatt numerikus apertúra: 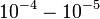 (ami elég rossz)
(ami elég rossz)
- bonyolult mintapreparáció
- feltöltődik a nemfém minta, elektron erősen kölcsönhat az atommal (erős rugalmas és rugalmatlan szórás)
- nem elég pontos pl. rácsparaméterek mérésére
Előny:
- sokmindent látni vele
- szűkíthető látótér
- korlátozott területű diffrakció valósítható meg
Szórás kinetikus elmélete
Röntgen sugárzás esetén 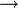 Thomson-szórás
Thomson-szórás
(1) Rugalmas szórás: 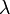 változatlan,
változatlan, 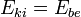
(2) Koherens
(3) Gyenge szórás: egyenes szórások…
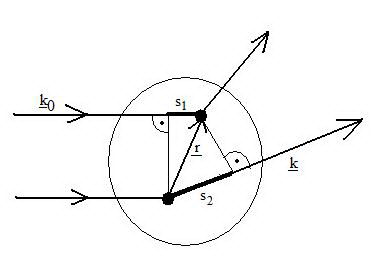
Fraunhofer interferencia:
A bemenő-kimenő hullámszám = 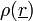 : ha nagy, nagy a szóródás; ha kicsi, kicsi a szóródás az adott pontban. (Röntgennél elektron-sűrűség, el.-mikroszkópnál el.- pot. sűrűség, neutronnál magsűrűség). A fáziskülönbség:
: ha nagy, nagy a szóródás; ha kicsi, kicsi a szóródás az adott pontban. (Röntgennél elektron-sűrűség, el.-mikroszkópnál el.- pot. sűrűség, neutronnál magsűrűség). A fáziskülönbség:
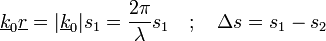
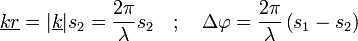
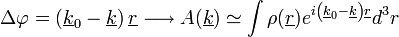
A(k) a szóródás, nem tudjuk mérni. A fenti integrál a sűrűségfv Fourier-transzformáltja.
Intenzitás: 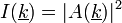
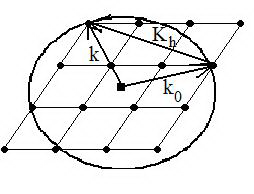
Bevezetjül az Ewald-szerkesztést: reciprokrácson berajzoljuk a beeső nyaláb k vektorát, majd húzunk a k vektor kezdőpontjából egy |k| sugarú gömböt, ez az Ewald-gömb.
- Jelölés:
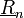 - rácsvektor;
- rácsvektor; 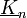 - reciprokrácsvektor
- reciprokrácsvektor
- Jelölés:
Mindezt felhasználva, a kristályos anyag elhajlási képe:
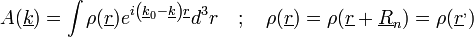
A fentiekből: 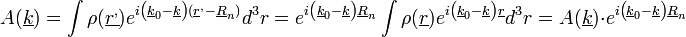
Tehát: 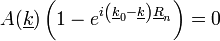
Azt szeretnénk, hogy A(k) ne legyen 0 (mivel azt keressük). Így a másik tagnak kell 0-nak lennie. Ezekből adódnak a következő tulajdonságok:
- 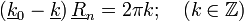
- 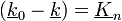
- 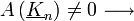 elhajlási irány
elhajlási irány
- 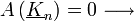 kioltás
kioltás
- 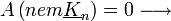 teljesülnie kell, különben nincs interferencia
teljesülnie kell, különben nincs interferencia
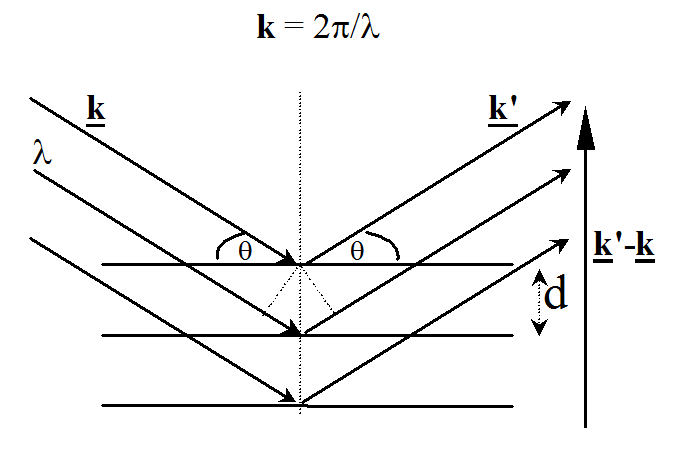
Bragg-feltétel
Az Ewald-szerkeztésből tudjuk, hogy 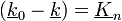
Továbbá tudjuk, hogy 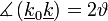
Tehát: 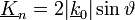
Az ábra alapján pedig látható, hogy: 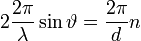
Amelyből átrendezéssel kapható a Bragg-feltétel: 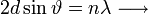 erősítés csak ebben az esetben lesz!
erősítés csak ebben az esetben lesz!
Különbség az elektron- és röntgendiffrakció között
A mai korszerű mikroszkópokban az elektronok energiája kb. 300keV, az elektronok hullámhossza 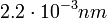 , ami nagyságrendekkel kisebb, mint a szokásos röntgenhullámhosszak. Ennek az a következménye, hogy a reciproktérban az Ewald-gömb sugara jóval nagyobb, így a Bragg-szög kicsi. A reciprokrács helyén az Ewald-gömb síknak tekinthető, ezért az elektrondiffrakciós felvételeken mindig a reciprokrács egy síkmetszetét láthatjuk, ellentétben a röntgendiffrakcióval, ahol a diffrakció képen köröket, illetve körszeleteket látunk. Azt, hogy tényleg több pont legyen diffrakciós helyzetben, az elektronmikroszkóp esetében az biztosítja, hogy a minta vékony, ezért a rácspontok Fourier-térbeli képe kiszélesedik(végtelen rácsnál lenne az pontszerű). Ez a kiszélesedés a röntgendiffrakciónál nem jelentős. Ott a Bragg-feltétel kielégítéséhez több módszer lehetséges. Pl. porszerű mintát használnak így a diffrakciós képen két kör metszéspontja lesz(hiszen a kristályok minden irányba orientáltak, így a reciprokrács is "velük forog"), vagy nem monokromatikus forrást használnak(Laue-elrendezés), hanem folytonos spektrumút, így a különböző hullámhosszak küllönböző rácsvektorokat hoznak diffrakciós helyzetbe.
, ami nagyságrendekkel kisebb, mint a szokásos röntgenhullámhosszak. Ennek az a következménye, hogy a reciproktérban az Ewald-gömb sugara jóval nagyobb, így a Bragg-szög kicsi. A reciprokrács helyén az Ewald-gömb síknak tekinthető, ezért az elektrondiffrakciós felvételeken mindig a reciprokrács egy síkmetszetét láthatjuk, ellentétben a röntgendiffrakcióval, ahol a diffrakció képen köröket, illetve körszeleteket látunk. Azt, hogy tényleg több pont legyen diffrakciós helyzetben, az elektronmikroszkóp esetében az biztosítja, hogy a minta vékony, ezért a rácspontok Fourier-térbeli képe kiszélesedik(végtelen rácsnál lenne az pontszerű). Ez a kiszélesedés a röntgendiffrakciónál nem jelentős. Ott a Bragg-feltétel kielégítéséhez több módszer lehetséges. Pl. porszerű mintát használnak így a diffrakciós képen két kör metszéspontja lesz(hiszen a kristályok minden irányba orientáltak, így a reciprokrács is "velük forog"), vagy nem monokromatikus forrást használnak(Laue-elrendezés), hanem folytonos spektrumút, így a különböző hullámhosszak küllönböző rácsvektorokat hoznak diffrakciós helyzetbe.
Rácsrezgések termikus hatásai.
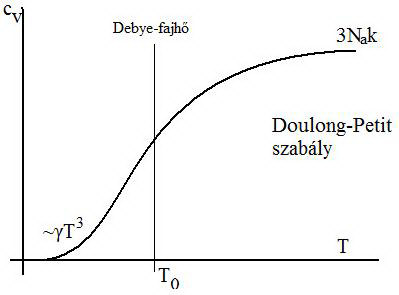
Debye-féle fajhő
- A rács termikus rezgéseit alacsony hőmérsékleten az Einstein-modell nem írja le elég jól, hiszen ez a modell minden atomot független oszcillátornak tekint. (Ezen számítások alapján az összenergia exp 0-hoz kellene, hogy tartson)
- Másik megközelítésben a rács normálrezgéseit a
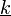 hullámszám-vektorral komponenseivel írjuk le. MInden részecskéhez hozzárendelhető egy ilyen vektor, és minden értékhez tartozik 3 módus (melyeknek más a polarizációs irányuk és ortogonálisak). Tehát egy N részecskéből álló redszerben 3N rezgési módus van (leszámítva a test mozgásából adódó 6 szabadsági fokot), melyeknek energiái kvantáltak
hullámszám-vektorral komponenseivel írjuk le. MInden részecskéhez hozzárendelhető egy ilyen vektor, és minden értékhez tartozik 3 módus (melyeknek más a polarizációs irányuk és ortogonálisak). Tehát egy N részecskéből álló redszerben 3N rezgési módus van (leszámítva a test mozgásából adódó 6 szabadsági fokot), melyeknek energiái kvantáltak 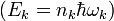 .
.
Foton: az elektromágneses sugárzási tér energiakvantuma.
Fonon: a kvantált rugalmas hullám vagy rácsrezgés energiakvantuma (a fotonhoz hasonlóan definiálva).
Debye-közelítésben 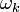 és
és 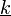 között a kapcsolatot nem a dinamikai összefüggésekből határozzuk meg, hanem a makroszkópikus kristály mozgásegyenletéből.
között a kapcsolatot nem a dinamikai összefüggésekből határozzuk meg, hanem a makroszkópikus kristály mozgásegyenletéből.
A belső energia várható értéke a következőképp adható meg: 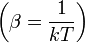
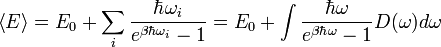
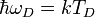 , ahol
, ahol 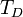 a Debye-hőmérséklet.
a Debye-hőmérséklet.
Hővezetés
A hővezetőképesség definíció szerint:
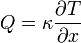 , ahol
, ahol
- Q - a termikus energiaáram
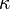 - a hővezetőképességi együttható
- a hővezetőképességi együttható
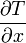 - a hőmérsékletgradiens
- a hőmérsékletgradiens
Tehát a termikus energia terjedése sztochasztikus folyamat és diffundálva terjed.
A kinetikus-gázelmélet alapján:
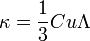 , ahol
, ahol
- C - az egységnyi térfogatra eső fajhő
- u - a részecske átlagsebessége
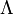 - részecske szabad úthossza (két ütközés között)
- részecske szabad úthossza (két ütközés között)
Debye ezt az összefüggést szilárd dielektrikumokra alkalmazta. Ekkor C a rácsrezgésekből (fononokból) adódó fajhő, u a hang terjedési sebessége és 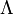 a fononok szabad úthossza.
a fononok szabad úthossza.
(pl a vákuum rövid távon rossz, hosszútávon jó hővezető)
Hőtágulás
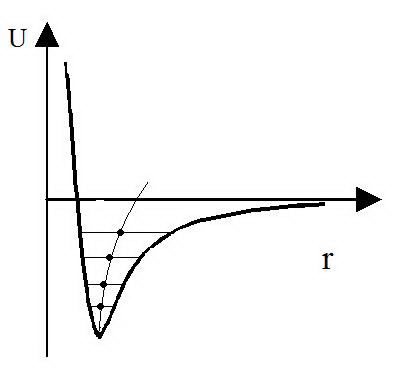
A hőtágulást a (potenciális energiában szereplő) nem lineáris tagok hozzák létre. (Pl: A kvarc erősen lineáris anyag – kevésbé hőtágul)
Az ábráról jól látható: ahogy nő a hőmérséklet, jobban rezegnek a részecskék, megnő az energia és így eltolódik a középpont, tehát távolabb kerülnek egymástól a részecskék. Ez a hőtágulás.
- ↑ Wikipédiáról: http://en.wikipedia.org/wiki/Bravais_lattice
- ↑ Képforrások: Kojnok József - Kondenzált anyagok fizikája gyakorlat fóliáiból (http://szft.elte.hu/~kojnok/szilfiz/szilfiz_gy.htm)
- ↑ Fonon: http://hu.wikipedia.org/wiki/Fonon