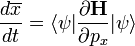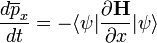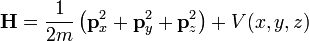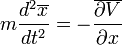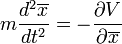A kvantummechanika elméleti háttere
A XIX. és XX. század fordulóján felhalmozódott kísérleti tapasztalatok abba az irányba mutattak, hogy az atomi szinteken mérhető fizikai mennyiségek a klasszikus szemlélettel szemben diszkrét értékeket vesznek fel folytonos helyett. Ez szükségessé tette olyan matematikai formalizmus bevezetését, amelytől nem idegen a diszkrét értékek megjelenése. Heisenberg, Dirac és Schrödinger voltak a formalizmus kialakulásának legnagyobb úttörői.
Tartalomjegyzék
- 1 A kvantummechanika matematikai alapjai
- 2 Analógia a Poisson-zárójelek és a kommutátorok között (*)
- 3 Kvantummechanikai reprezentációk
- 4 A hullámfüggvény valószínűségi értelmezése
- 5 A Schrödinger-egyenlet
- 6 Heisenberg-kép
- 7 Határozatlansági-elv
- 8 Az energia-idő határozatlansági reláció
- 9 Hullámcsomag
- 10 Az impulzusmomentum operátor
- 11 A Schrödinger-egyenlet szeparálása
- 12 A spin és a Pauli-egyenlet
- 13 Korrespondencia-elv, Ehrenfest-tétel
- 14 EPR-paradoxon, Bell-egyenlőtlenség
A kvantummechanika matematikai alapjai
A kvantummechanikában a fizikai mennyiségekhez operátorokat rendelünk. Az általunk mérhető értékeket a fizikai mennyiség operátorának sajátértékeivel azonosítjuk. Mivel az általunk mért értékek valósak, ez azonnal megkötést ad az operátorokra: azoknak önadjungáltaknak kell lenniük:
Az adjungált operátorra definíció szerint:
a Hilbert-tér bármely u,v elemeire. Ez mátrixreprezentációban a transzponált komplex konjugáltját jelenti.
A klasszikus mechanikában a kanonikus formalizmus igen koherens és logikus tárgyalásmódot jelentett, ezért ezt tovább visszük axióma szerűen a kvantummechanikában, és megköveteljük a klasszikusan fennálló kanonikus relációk teljesülését. Klasszikusan az anyagi rendszer helykoordinátákkla jellemezzük, az impulzust a a helykoordinátákhoz konjugált mennyiségként vezetjük be:
Axiomatikusan megköveteljük, hogy a hely és az impulzus operátora teljesítse a következő, Heisenberg-féle felcserélési relációkat:
Itt a [a, b] = ab - ba, kommutátor, 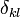 pedig a Kronecker-delta.
pedig a Kronecker-delta.
Analógia a Poisson-zárójelek és a kommutátorok között (*)
A klasszikus mechanikából ismert Poisson-zárójelek szerepe nagyon hasonlít a kvantummechanikai kommutátorokéhoz, hiszen ha visszaemlékszünk:
A Poisson-zárjelekkel felírva egy mennyiség időfejlődését a kötekezőt kapjuk:
ahol a Poisson-zárójel definíciója:
ahol a és b az általánosított kooridnáták és impulzusok függvénye.
Ez kísértetiesen hasonlít a kvantummechanikai Heisenberg-képben az operátorok időfejlődését leíró egyenletre (lásd lejjebb).
Kvantummechanikai reprezentációk
A fenti megkötéseket többféle reprezentációban ki lehet elégíteni, Schrödinger hullámmechanikát épített rá, Heisenberg hermitikus mátrixokkal dolgozott. Elvileg integráloperátorokat is használhatnánk, de azokkal bonyolult számolni. Tradícionálisan a differenciál-egyenletek megoldási apparátusa volt készen, ezért ezzel dolgoztak nagyon sokáig. Később megmutatták, hogy a különböző tárgyalásmódok ekvivalensek. A továbbiakban a Schrödinger-féle reprezentációban dolgozunk. Schrödinger a következő operátorokat vezette be:
Ennek akkor van értelme, ha az operátorok valamilyen folytonos függvényre hatnak. Ezért ebben a reprezentációban a rendszert a koordinátáktól függő hullámfüggvénnyel adjuk meg. Belátható, hogy a bevezetett felcserélési relációkat teljesítik a bevezetett operátorok. A bevezetett hullámfüggvényre további megkötéseink vannak, ha A valamilyen fizikai mennyiség operátora, akkor fennáll a következő sajátérték-egyenlet:
Ennek csak azon 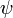 megoldásait fogadjuk el, amelyek egyértékűek, folytonosak, és négyzetesen integrálhatóak, ezeket a függvényeket nevezhetjük reguláris függvényeknek. A továbbiakban a reguláris megoldásokra, mint sajátfüggvényre, az ezekhez tartozó
megoldásait fogadjuk el, amelyek egyértékűek, folytonosak, és négyzetesen integrálhatóak, ezeket a függvényeket nevezhetjük reguláris függvényeknek. A továbbiakban a reguláris megoldásokra, mint sajátfüggvényre, az ezekhez tartozó 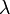 paraméterekre, mint sajátértékekre hivatkozunk.
paraméterekre, mint sajátértékekre hivatkozunk.
A hullámfüggvény valószínűségi értelmezése
A rendszer állapotára bevezettük a hullámfüggvényt: 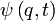 . Ennek abszolút érték négyzete meghatározza a koordinátaértékek valószínűségének eloszlását, másképpen
. Ennek abszolút érték négyzete meghatározza a koordinátaértékek valószínűségének eloszlását, másképpen 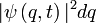 meghatározza, hogy a dq elemben mekkora a valószínűsége a q koordinátaértékek előfordulásának. Speciálisan pontrendszerek esetén visszakapjuk a klasszikus koordinátavektorokkla való jellemzést:
meghatározza, hogy a dq elemben mekkora a valószínűsége a q koordinátaértékek előfordulásának. Speciálisan pontrendszerek esetén visszakapjuk a klasszikus koordinátavektorokkla való jellemzést: 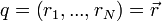 . Ez az értelmezés, hozzávéve azt a tapasztalatot, hogy egy részecskét az ideális detektor valahol mindig megtalál, adja a normálási feltételt, vagyis hogy a hullámfüggvény teljes térre vett integrálja 1.
. Ez az értelmezés, hozzávéve azt a tapasztalatot, hogy egy részecskét az ideális detektor valahol mindig megtalál, adja a normálási feltételt, vagyis hogy a hullámfüggvény teljes térre vett integrálja 1.
Koppenhágai axiómák
A fentiek szerint a hullámfüggvény valószínűséget ír le, és a fizikai operátorok rajta sajátértéket vesznek fel méréskor. Ezen fogalmak összekapcsolásának értelmezésére a következőket vezetjük be:
- Ha adott fizikai mennyiséget akarunk megmérni, az eredmény csak annak valamely sajátértéke lehet.
- Ha többszöri mérést végzünk, és a rendszer a fizikai operátor sajátállapotában van, akkor a sajátállapothoz tartozó sajátértéket mérjük, ha nincs sajátállapotban, akkor a hullámfüggvényt ki kell fejteni a sajátértékek bázisán, és a kifejtési együtthatók négyzetei adják az adott sajátértékek mérésének valószínűségeit:
A kvantummechanika mértékinvarianciája
A 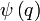 és
és 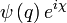 hullámfüggvényt fizikai szempontból egyenértékűnek tekintjük mivel abszolút értékük megegyezik,
hullámfüggvényt fizikai szempontból egyenértékűnek tekintjük mivel abszolút értékük megegyezik, 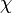 egy tetszőleges függvény. Ezen transzformációk az U(1) csoportot alkotják.
egy tetszőleges függvény. Ezen transzformációk az U(1) csoportot alkotják.
A Schrödinger-egyenlet
(*A levezetés csak a kitekintés kedvéért szerepel itt)
Az axiomatikus felépítésben érdemes megjegyezni, hogy igen kevés alapfeltevésből eljuthatunk a kvantummechanika talán legalapvetőbb egyenletéhez, a Schrödinger-egyenlethez. Az előzőekben bevezettük a hullámfüggvényt. Erre a sajátérték egyenlet alapján kiróttuk a regularitást, amely alapján a függvény négyzetesen integrálható. Teljesen jogosan várhatjuk el, hogy ez minden időpillanatban teljesüljön a hullámfüggvényre, azaz az időfejlődés megtartja a normát. Vezessünk be egy kezdetben tetszőleges G(t) időfejlesztő operátort. Ez az operátor a hullámfüggvényt t idővel későbbi állapotába viszi át. Követeljük meg, hogy ez a transzformáció független legyen attól, hogy ez az eltolás milyen kezdőponthoz képest törénik, azaz legyen időeltolási szimmetria. Ez teljesen analóg a klasszikus mechanikánál tapasztaltakkal. Végül követeljük meg, hogyha két egymás utáni transzformációt (időfejlesztést, pl 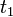 és
és 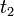 ) végzünk, az ekvivalens legyen egyetlen, az időkülönbségek összegével jellemzett időfejlesztéssel (
) végzünk, az ekvivalens legyen egyetlen, az időkülönbségek összegével jellemzett időfejlesztéssel (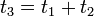 ). Másszóval az időfejlődés egyparaméteres csoportot alkot. A fentiekből némi algebrai átalakításokkal, és a normafeltétel kihasználásával belátható, hogy a G operátor unitér, azaz az adjungáltja az inverzével egyenlő. További algebrai átalakításokkal, és az egyparaméteres csoportok azon tulajdonságát kihasználva, hogy felírhatóak egy másik exponencializált operátor segítésével kapjuk a következő összefüggést:
). Másszóval az időfejlődés egyparaméteres csoportot alkot. A fentiekből némi algebrai átalakításokkal, és a normafeltétel kihasználásával belátható, hogy a G operátor unitér, azaz az adjungáltja az inverzével egyenlő. További algebrai átalakításokkal, és az egyparaméteres csoportok azon tulajdonságát kihasználva, hogy felírhatóak egy másik exponencializált operátor segítésével kapjuk a következő összefüggést:
G unitérségéből belátható, hogy Z anti-hermitikus, azaz sajátértékei tisztán képzetesek. Vezessük be ennek az operátornak az i-szeresét, ez már hermitikus lesz, és a sajátértékei valósak lesznek:
Mivel t dimenziója s, ezért S dimenziójának 1/s-nek kell lennie. Önkényesen bevezethetünk egy másik hermitikus operátort, amelynek a dimenziója Joule:
Ekkor G alakja:
Egy tetszőleges 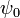 kezdőfeltételből indítva:
kezdőfeltételből indítva:
Deriváljuk ezt le idő szerint, és szorozzuk be 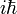 -al:
-al:
Ez az egyenlet a Schrödinger-egyenlet. Itt azonban még nem derült ki, hogy H micsoda. Belátható, hogy ez a Hamilton-operátora lesz a vizsgált rendszernek. Az így nyert egyenlet lineáris, azaz a hullámfüggvényre érvényes a szuperpozíció elve: ha 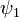 és
és 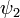 a rendszer lehetséges állapotai akkor
a rendszer lehetséges állapotai akkor 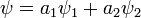 is az. Továbbá feltsszük, hogy
is az. Továbbá feltsszük, hogy 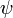 és
és 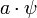 ugyanazt az állapotot írja le (a valós). Ezek közül a normálással tudunk kiválasztani egyet.
ugyanazt az állapotot írja le (a valós). Ezek közül a normálással tudunk kiválasztani egyet.
Heisenberg-kép
Az előző levezetésben természetesen adódott, hogy a hullámfüggvény időfüggő, és ezért nem volt szükség arra, hogy az operátorokról feltegyük, hogy időfüggőek. Ezt a tárgyalásmódot, hogy az időfüggés a hullámfüggvényben van Schrödinger-képnek nevezzük. Vizsgáljuk meg egy A operátor időátlagát:
Itt bevezettük a bra-ket jelölés rendszert. Írjuk be az időfüggő hullámfüggvényeket mint a kezdőállapot és az arra ható időfejlesztő unitér operátort G szorzatát:
A belső operátor szorzatot elnevezhetjük egy új időfüggő operátornak. Ezt az időfüggő operátort tekinthetjük A Heisenberg-képbeli reprezentációjának. Az operátorok időfüggését leíró egyenlet:
Határozatlansági-elv
Ha adott egy operátor, amelyet hattatva a rendszer hullámfüggvényére az sajátértéket vesz fel, akkor azt mondjuk, hogy az az operátor sajátállapota, ekkor az értéke határozott, a sajátértéket veszi fel. Ha ez nem teljesül, azaz a hullámfüggvényen nem vesz fel az operátor sajátértéket, ekkor az értéke határozatlan. Ha két operátor kommutál, akkor létezik olyan hullámfüggvény, amelyen mindkettő sajátértéket vesz fel. Azok az operátorok, amelyek egymással nem kommutálnak egy igen alapvető összefüggésnek tesznek eleget. Definiáljuk a közepes eltérést:
Ekkor két hermitikus operátorra fennáll, hogy:
Szavakban megfogalmazva: két felnemcserélhető operátor értékét nem lehet egyszerre tetszőleges pontossággal megmérni. Mérésnek tekintünk minden folyamatot, ahol klasszikus és kvantumos objektumnak történik kölcsönhatása. A mérésnek elvi korlátja van. Ezt az összefüggést nevezzük Heisenberg-féle határozatlansági relációnak. A leghíresebb a hely és impulzusra vonatkozó reláció:
Az energia-idő határozatlansági reláció
Az energia és idő közti határozatlansági reláció az előző sémába nem illik bele, mert az időnek nincs operátora. A kvantummechanika korai alapítóinak is világos volt, hogy egy
alakú reláció fennáll, de nem volt rögtön világos, hogy mi 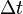 . A gyakorlatban ez a reláció pl. azt jelenti, hogy egy rövid életidejű állapot energiája csak nagyon gyengén határozott. Az állapot élettartama azonban nem egy, az állapothoz rendelhető operátor. Egy valamivel precízebb megfogalmazás a következő. Egy
. A gyakorlatban ez a reláció pl. azt jelenti, hogy egy rövid életidejű állapot energiája csak nagyon gyengén határozott. Az állapot élettartama azonban nem egy, az állapothoz rendelhető operátor. Egy valamivel precízebb megfogalmazás a következő. Egy 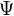 állapotban egy B mennyiségre fennáll a következő reláció:
állapotban egy B mennyiségre fennáll a következő reláció:
Hullámcsomag
A részecskék hullámtermészete a de Broglie hipotézis óta benne volt a levegőben(lásd A kvantumelmélet alapvető kísérletei). A Schrödinger-egyenletnek vannak síkhullám megoldásai, de ezek nyilván nem azonosíthatóak egy részecskével, mert egyáltalán nem lokalizáltak. A síkhullám-megoldásokból azonban hullámcsomag alkotható, matematikailag egy Fourier-integrál formájában. Az egyszerűség kedvéért egy dimenzióban:
Ezen integrál értéke azokon a pontokon lesz nagy, ahol az exponenciális tag nem túl erősen oszcillál, hiszen ha túl erős az oszcilláció, az integrál kiegyenlítődik és nullát kap. Tehát ott lesz nagy az integrál, ahol 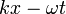 közel konstans, vagyis:
közel konstans, vagyis:
Ez hasonlít a tömegpont x=vt képletére, így a klasszikus sebesség hullámmechanikai megfelelője a csoportsebesség:
Az impulzusmomentum operátor
Klasszikusan az impulzusmomentum a kövektező összefüggéssel van definiálva:
Ezt visszük át az operátoros reprezentációba, a hely és impulzus operátorokat beírva. Egyszerű behelyettesítésekkel igazolhatóak az alábbi képletek (amelyek nem csak a z komponensre állnak fennt, a többire csak permutálni kell az indexeket):
L felcserélhető bármelyik komponensével. Ebből következik, hogy van közös sajátfüggvényük. Polárkoordinátás áttérés után a sajátérték probléma megoldható, eredményül megkapjuk a sajátfüggvényeket és a sajátértékeket. A z komponensre:
Az impulzusmomentum négyzetére:
Itt P a módosított Legendre-polinomot jelöli, maga a sajátfüggvény az úgynevezett gömbfüggény, amely a két térbeli szög, és két másik egészszám függvénye. Ez utóbbiak felelnek meg mágneses- és mellékkvantumszámnak a hidrogénatom esetében.
A Schrödinger-egyenlet szeparálása
Amikor a Schrödinger-egyenletet centrális potenciálban oldjuk meg, a potenciál cska a sugár abszolutértékétől függ. Polárkoordinátás tárgyalásban érezhető, hogy a sugárfüggő rész leválasztható a szögfüggő résztől. Ez valóban így van, a hullámfüggvénynek van szorzatalakú megoldása, amelyben a sugárfüggés leválasztódik. A Schrödinger-egyenletbe visszaírva az két egyenletre esik szét. A szögfüggés az impulzusmomentumnál bevezetett sajátfüggvényeket (gömbfüggvények) és sajátértékeket adja, ez tehát minden centrális erőteres problémára ugyanaz. Egy speciális potenciálra, a hidrogénatomra, az integrálható problémáknál kidolgozzuk a megoldást.
A spin és a Pauli-egyenlet
A kísérleti bevezetőben említésre került Stern-Gerlach-féle kísérlet, amely tulajdonképpen a benne áthaladó részecskék impulzusmomentumát méri. A kísérletek csak úgy értelmezhetőek ellentmondásmentesen, ha feltételezzük, hogy a részecskéknek van saját impulzusmomentumuk is. Ezt spinnek nevezzük, és az S operátort rendeljük hozzá.
Az eddigi tárgyalásokban nem voltunk tekintettel erre a mennyiségre. Tudjuk, hogy van a részecskéknek impulzusmomentuma (L), ezt megkülönböztetésül pályamomentumnak nevezzük mostantól. A két momentum összegére bevezetjük a teljes impulzusmomentumot:
J = L + S. A pályamomentumnak ismertek a sajátértékei, a spinről pedig a kísérletek alapján belátható, hogy két féle értéke lehet: 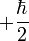 és
és 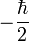 .
.
A mágneses hatás leírásához a pályanyomatéknál elég volt a klasszikus analógia:
A spinhez tartozó mágneses momentumot a kísérletek alapján:
definiálja. Ezt a Schrödinger-egyenlet nem tartalmazza, azonban a pontos leíráshoz szükséges ennek figyelembevétele. Mivel a spin kétféle értéket vehet fel, és érvényes a szuperpozíció elve, ezért bevezetünk két rész-hullámfüggvényt amelyek lineárkombinációja adja a teljes hullámfüggvényt, az együtthatók pedig a spinsajátfüggvények (pl.: (1, 0) és (0, 1) ha vektorként reprezentáljuk őket). A mágnesestérrel való kölcsönhatást klasszikus analógia alapján adjuk hozzá a Schrödinger-egyenlethez. Ismert klasszikus mechanikából a ponttöltés mozgásegyenlete (H a mágneses tér):
Belátható, hogy ezt a mozgásegyenletet előállító Hamilton-függvény (ez most másik H):
Ezt operátorrá alakítva betesszük a Schrödinger-egyenletbe, és a hullámfüggvényként a spint is figyelembe vevő hullámfüggvényt tekintjük:
Az így kapott egyenlet a Pauli-egyenlet. Felbukkantak a Pauli-mátrixok (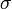 , pontosabban a képletben a 3 mátrixból képzett vektor áll, és a mellette zárójelben szereplő mennyiséggel skalárisan kell szorozni, hiszen az is egy vektor). Ezek a spinnek az algebrájában szerepet játszó 2x2-es mátrixok, velük írhatóak fel a spinoperátorok is:
, pontosabban a képletben a 3 mátrixból képzett vektor áll, és a mellette zárójelben szereplő mennyiséggel skalárisan kell szorozni, hiszen az is egy vektor). Ezek a spinnek az algebrájában szerepet játszó 2x2-es mátrixok, velük írhatóak fel a spinoperátorok is:
A mátrixok explicit alakjait lásd itt.
Korrespondencia-elv, Ehrenfest-tétel
Az eddigiekből látható, hogy a kvantummechanika működése és felépítése nagyban különbözik a klasszikus leírástól, a klasszikus törvények nem alkalmazhatóak változatlanul a mikrovilág leírására. Azonban a kvantumelméletet, mint mélyebb elméletet tekintve felmerül a kérdés, hogy nem tartalmazza-e valamilyen módon a klasszikus törvényeket. A válasz az, hogy igen, a klasszikus rendszerek felfoghatóak sok kvantumszámú összetett rendszerekként, ezért a kvantumosan megfogalmazott törvényeknek nagy kvantumszámokra történő (illetve a Planck-állandóval zérushoz tartó) határátmeneteit kell ekkor vizsgálnunk, és az állítás az, hogy ekkor visszkapjuk a megfelelő klasszikus törvényeket. Ezt az állítást korrespondencia-elvnek (megfeleltetési-elv) nevezzük, és megfogalmazása Niels Bohr nevéhez kötődik.
A korrespondencia-elv egyik ékes bizonyítéka az Ehrenfest-tétel. Tekintsük egy fizikai mennyiség operátorának várható értékét:
Számoljuk ki ennek időbeli változását a Schrődinger-egyenlet alapján. Ekkor levezethető, hogy abban az esetben, amikor az operátor nem függ az időtől (minden időfügés a hullámfüggvény változása miatt történik), akkor a követekző formula érvényes:
Ha O helyére a hely vagy az impulzus operátorát írjuk, a következő ismerős összefüggéseket kapjuk:
Ezek a klasszikus mechanikából ismert kanonikus egyenletek.
Ha egy pontrészecske mozgását leíró Hamilton-operátort tekintjük, amely potenciált is tartalmaz:
Akkor a helykoordinátákra a következő kifejezés adódik:
A baloldalon a gyorsulás, a jobboldalon a ható erő ismerhető fel, azaz visszakaptuk a Newton-törvényt. Amennyiben a potenciál lassan változik, sorfejtést alkalmazhatunk 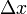 szerint, és akkor a következő eredményt kapjuk:
szerint, és akkor a következő eredményt kapjuk:
azaz lassan változó potenciál esetén elég a koordináta értékeket átlagolni. Tulajdonképpen ez felel meg a klasszikus törvényeknek: amikor a távolságok kicsik a változó potenciálváltozáshoz képest, akkor beszélhetünk klasszikus részecskéről, mert nem követünk el nagy hibát (a sorfejtésben csak a vezető tag nagy), azonban atomi mércén már számos tag jelentős a sorfejtésben, ekkor a klasszikus számolási menet használhatatlan. Az Ehrenfest-tétel tehát az operátor várható értékén keresztül kapscsolatot teremt a klasszikus mechanika és a kvantummechanika között, egyben behatárolva az előbbi érvényességi körét.
EPR-paradoxon, Bell-egyenlőtlenség
A kvantummechanika furcsaságainak és klasszikus gondolkodással szembenálló működésének egyik leglátványosabb példája az Einstein-Podolsky-Rosen által felvetett gondolat kísérlet és annak interpretációja. A gondolatkísérlet egy összefonódott, eltávolodó kvantummechanikai rendszerre vonatkozik (például bomlásban keletkező két ellentétes spinű részecske, vagy két ellentétes polarizációval szétrepülő foton). A felvetés arra összpontosul, hogy mitörténik amikor megakarjuk mérni a valamely fizikai jelelmzőt, amelyre a teljes rendszerben megmaradási törvény érvényes (azaz, ha tudnánk az egyik "rész" értékét, például spinjét, abból meghatározható lenne a másiké).
A mérési problematikát Einsteinék a következő két lehetőségben foglalták össze:
- Vagy az egyik rendszeren végzett mérésnek hatása van a másik B rendszerre, és ezáltal egyetlen méréssel meghatározható mindkét rész állapota
- Vagy van valami olyan rejtett tulajdonság, amelyet a kvantummechanika nem vesz figyelembe, ezért nem teljes a leírásunk a jelenségről, és ez határozza meg, hogy mit is fogunk mérni.
Az első lehetőség a relativitás elmélettel, és a kauzalitással lenne ellentmondásban, a második rejtett paraméterek bevezetését tenné szükségessé, amelyek a kvantummechanikánál mélyebb elméletre utaló jelek lennének.
Az első nyilván tarthatatlan, a kauzalitást eddig minden tapasztalatunk igazolta, ezért a második állítást kezdték el részletesen vizsgálni. Amennyiben létezik rejtettparaméteres elmélet, akkor annak is kell jóslatokat adnia egyes mérehető mennyiségekre, ugyanígy a kvantummechanika is ad jóslatokat. Levezethető, hogy például két kimenetű kísérletekben két mérhető mennyiség korrelációjára általános limit adható (a háromszög egyenlőtlenség felhasználásával), ez a limit vezet a Bell-egyenlőtlenséghez. Ugyanakkor a kvantummechanikából is levethető a két mennyiség korrelációja. Az eredmények vizsgálatával azt látjuk, hogy egyes esetekben a kvantummechanika sérti a rejtettparamáteres moellre fennálló limiteket, azaz az előbbi nem lehet konzisztens alap a kvantumelmélet leírásához!
A gyakorlatban a Bell által levezetett egyenlőség kevésbé használható (nehezebb ilyen kísérletet készíteni), heleytte az általánosabb (általánosabb rejtett paraméteres modelleket magábanfoglaló) CHSH egyenlőtlenség használatosatos.
A kísérletek elvégzésével megmérhetők a korrelációk a valóságban is. Az eredmény: a kvantummechanikai leírás minden esetben helyes jóslatot ad.
Ezek alapján nem konstruálható rejtettparaméteres modell, és elvetettük a távolhatás lehetőségét is. Ezek után felmerül a kérdés, hogy mi a helyzet az EPR paradoxonnal? A válasz az, hogy rossz a kérdésfelvetés. A paradoxon oka, hogy a kvantummechanikai rendszernek NINCS részrendszere! Nem beszélhetünk a részrendszernek állapotáról, mennyiségeiről, a részrendszerek össze vannak fonódva, csak együtt tárgyalhatók. resume
A történet tovább bonyolítható, problémák jelentkeznek abban, hogy a kvantummechanikai valószínűség fogalom kissé eltér a Kolmogorovi klasszikus valószínűség fogalomtól. Ha hozzávesszük azt is, hogy a kvantummechanikai valószínűségek nem tekinthetők önálló eseményekként, hanem valamilyen korábbi kiváltó okokkal állnak kapcsolatban feltételes valószínűségeken keresztül, akkor létesíthető olyan rejtett paraméteres modell, amelyet nem sértenek a kísérletek, és a kvantummechanikai jóslatok, ez a gondolatmenet azonban teljes determinizmushoz vezet.
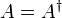
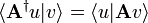
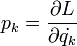
![[p_k, q_l] = \frac{\hbar}{i} \mathbf{I} \delta_{kl}](/images/math/9/6/b/96bc74a7762d2b04e7d4ddb95491b008.png)
![[p_k, p_l] = 0\,](/images/math/7/8/0/78016cf169e11fca509ca945ee8b65d2.png)
![[q_k, q_l] = 0\,](/images/math/1/a/d/1ad0be889512110d2405c98676b76a0a.png)
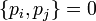
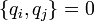
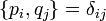
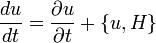
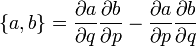
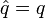
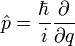
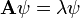
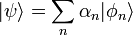
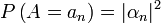
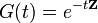
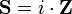
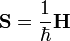
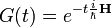
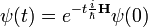
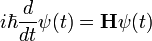
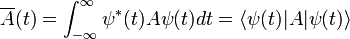
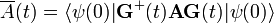
![\frac{dA}{dt}=\frac{i}{\hbar}[H,A]+\frac{\partial A}{\partial t}](/images/math/a/b/a/aba3492c13e6b29b3ff04b8b81b6fd30.png)
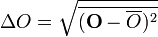
![\Delta O_1 \Delta O_2 \geq \frac{1}{2}|\overline{[\mathbf{O}_1,\mathbf{O}_2]}|](/images/math/d/8/a/d8a20f6e79a0d9790aec79b985b2cead.png)
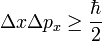
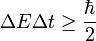
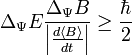
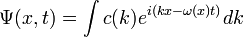
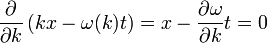
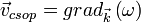
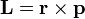
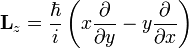
![[\mathbf{L}_x, \mathbf{L}_y] = i \hbar \mathbf{L}_z](/images/math/b/7/b/b7b11ff39da61036729e909c8694d0c9.png)
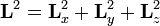
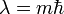
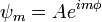
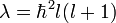
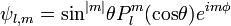
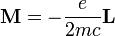
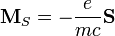
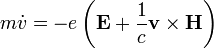
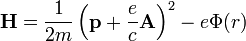
![i \hbar \frac{d}{dt} \psi(t) = \left[ \frac{1}{2m} \left( \sigma \left(\mathbf{p} + \frac{e}{c}\mathbf{A} \right)\right)^2 - e\Phi(r) \right] \psi(t)](/images/math/3/b/6/3b6d405b8bef35ab5e78fa19d1df302c.png)
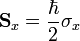
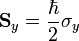
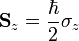
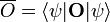
![\frac{ d \overline{O}}{dt} = \frac{i}{\hbar} \langle \psi | [ \mathbf{H}, \mathbf{O}] | \psi \rangle](/images/math/4/f/3/4f3844a7902bc8f99bc3062baf999e97.png)