Kvantumstatisztikák
Tartalomjegyzék
- 1 Bevezetés, ideális gázok, Fermi- és Bose-eloszlás
- 2 Bose-Einstein kondenzáció
- 3 Hőmérsékleti sugárzás, Stefan-Boltzmann törvény
- 4 Fononok, szilárdtestfizikai alkalmazások (diszperziós reláció)
- 5 Degenerált Fermi-gáz
- 6 Elektronfajhő, kvantumkorrekciók. {Bethe-Sommerfeld sorfejtés, Landau-paramágnesség}
Bevezetés, ideális gázok, Fermi- és Bose-eloszlás
Egy sokrészecskés kvantummechanikai rendszert a hullámfüggvénye ír le, ami összes részecske összes koordinátájától, és egyéb, belső szabadsági fokot leíró változójától (pl.: spin) is függ. Egy fizikai mennyiség várható értéke az operátorával vett szendiccsel számítható ki: 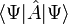 . Bármilyen hullámfüggvény kifejezhető például az időfüggetlen Scrödinger-egyenlet megoldásaival, amik a rendszer energiasajátállapotai. Véges méretű rendszernél ezekből általában megszámlálhatóan sok van, így a hullámfüggvény egy (véges vagy végtelen) összeggel adható meg:
. Bármilyen hullámfüggvény kifejezhető például az időfüggetlen Scrödinger-egyenlet megoldásaival, amik a rendszer energiasajátállapotai. Véges méretű rendszernél ezekből általában megszámlálhatóan sok van, így a hullámfüggvény egy (véges vagy végtelen) összeggel adható meg:  Itt
Itt 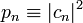 a valószínűsége annak, hogy a rendszeren mérést végezve azt az
a valószínűsége annak, hogy a rendszeren mérést végezve azt az 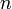 -edik sajátállapotban találjuk. Így ha megadjuk a rendszer hullámfüggvényét egy pillanatban, akkor azzal megadtuk a rendszert leíró valószínűségeloszlást is. A rendszer entrópiája a klasszikus rendszerekhez hasonlóan
-edik sajátállapotban találjuk. Így ha megadjuk a rendszer hullámfüggvényét egy pillanatban, akkor azzal megadtuk a rendszert leíró valószínűségeloszlást is. A rendszer entrópiája a klasszikus rendszerekhez hasonlóan 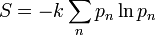 A klasszikus rendszerekkel szemben, ahol a rendszer energiája egy tartományon belül folytonosan változhatott, itt az energia (és így a rendszert leíró többi mennyiség is) megszámlálhatóan sok diszkrét értéket vehet fel. Sokrészecskés rendszernél általában az energiasajátértékek degeneráltak, és nagyon sok van belőlük, így az összegzést gyakran integrállal lehet helyettesíteni.
A klasszikus rendszerekkel szemben, ahol a rendszer energiája egy tartományon belül folytonosan változhatott, itt az energia (és így a rendszert leíró többi mennyiség is) megszámlálhatóan sok diszkrét értéket vehet fel. Sokrészecskés rendszernél általában az energiasajátértékek degeneráltak, és nagyon sok van belőlük, így az összegzést gyakran integrállal lehet helyettesíteni.
A továbbiakban kölcsönhatás nélküli kvantumgázokkal foglalkozunk. Ekkor a részecskék közül mindegyikre ugyanaz az egyrészecskés Schrödinger-egyenlet vonatkozik, az ennek megoldásaként adódó egyrészecskés energiasajátállapotok minden részecskére ugyanazok, így (mivel a részecskék megkülönböztethetetlenek) a rendszer leírásához elég azt leírni, hogy melyik egyrészecske sajátállapotban hány részecske van. Fermionoknál ehhez hozzá kell tenni még azt a feltételt, hogy egy energiasajátállapotban legfeljebb egy részecske lehet, bozonoknál akármennyi. A kvantumgázoknál általában nagykanonikus sokaságban érdemes dolgozni, mert így az állapotösszeg és a belőle számítható mennyiségek kiszámításakor nem kell a részecskék számára vonatkozó mellékfeltételt figyelembe venni, ami egyszerűsíti a számításokat. Ekkor a részecskeszámot és a többi mennyiséget is a kémiai potenciál függvényében kell kiszámítani, az így kapott eredményekből a kémiai potenciál kiküszöbölésével lehet a gáz állapotegyenletét meghatározni, ez azonban analítikusan nem végezhető el.
A Bose-Einstein-eloszlás
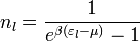 megadja az
megadja az 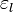 energiájú állapotban levő részecskék várható értékét.
Ahhoz, hogy ez sehol se divergáljon és a részecskék száma pozitív legyen, az szükséges, hogy a kémiai potenciál kisebb legyen a legalacsonyabb energiaszintnél (így a nevezőben mindig egy pozitív szám lesz).
energiájú állapotban levő részecskék várható értékét.
Ahhoz, hogy ez sehol se divergáljon és a részecskék száma pozitív legyen, az szükséges, hogy a kémiai potenciál kisebb legyen a legalacsonyabb energiaszintnél (így a nevezőben mindig egy pozitív szám lesz).
A Fermi-Dirac-eloszlás
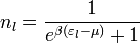 megadja az
megadja az 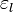 energiájú állapotban levő részecskék várható értékét.
A Fermi-eloszlás értéke mindig egy 0 és 1 közötti szám.
energiájú állapotban levő részecskék várható értékét.
A Fermi-eloszlás értéke mindig egy 0 és 1 közötti szám.
Ideális gázok
Egy 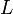 oldalú kockába zárt ideális gáznál az energisajátállapotok:
oldalú kockába zárt ideális gáznál az energisajátállapotok:
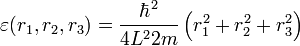 Itt a három
Itt a három  egész értékeket vehet fel.
Az eloszlásfüggvények segítségével kiszámíthatjuk a részecskeszámot és az energiát.
egész értékeket vehet fel.
Az eloszlásfüggvények segítségével kiszámíthatjuk a részecskeszámot és az energiát.
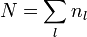
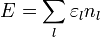
A nyomás a nagykanonikus potenciálból származtatható:
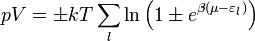
A felső előjel vontatkozik a fermionokra, az alsó a bozonokra.
A fenti összegzések (azt feltételezve, hogy nagyon sok energiaszint van és ezek egymáshoz közel helyezkednek el) integrállal közelíthetőek, az eredmények:
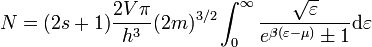
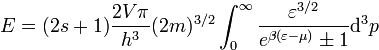
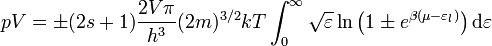
Itt  a részecskék spinje,
a részecskék spinje, 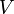 a gáz térfogata, és
a gáz térfogata, és 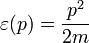 egy részecske energiája. A nyomás kifejezését parciálisan integrálva kapjuk, hogy:
egy részecske energiája. A nyomás kifejezését parciálisan integrálva kapjuk, hogy:
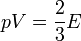
A klasszikus határeset
Mindkét eloszlásnak a klasszikus határesete a Boltzmann eloszlás. Ha a számlálóban levő exponenciális tag nagy, akkor mellette az 1 elhanyagolható, és pont a Boltzmann eloszlást kapjuk. (Természetesen ekkor mindegyik állapotban a részecskék számának várható értéke nagyon kicsi, majdnem 0.) Legyen az alapállapot energiája 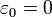 (az alapállapoti energiát tetszőlegesen eltolhatjuk, mert nem mérhető), a részecskék energiája:
(az alapállapoti energiát tetszőlegesen eltolhatjuk, mert nem mérhető), a részecskék energiája: 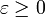 . Ekkor annak a feltétele, hogy az eloszlásban szereplő exponenciális értéke minden energiaszintre nagy legyen annak felel meg, hogy
. Ekkor annak a feltétele, hogy az eloszlásban szereplő exponenciális értéke minden energiaszintre nagy legyen annak felel meg, hogy 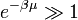 teljesüljön. Klasszikus ideális gázra:
teljesüljön. Klasszikus ideális gázra:
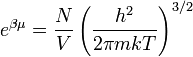
Ezzel az előző feltétel:
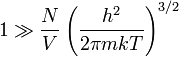
Azaz az előző feltétel annak felel meg, hogy elég magas legyen a hőmérséklet és elég kicsi legyen a gáz sűrűsége. Ugyanezt az eredményt kapjuk a határozatlansági reláció felhasználásával is. Klasszikus esetben 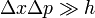 , a koordináta és impulzusbizonytalanságokról pedig feltételezzük, hogy kisebbek, mint azok átlagos értékei:
, a koordináta és impulzusbizonytalanságokról pedig feltételezzük, hogy kisebbek, mint azok átlagos értékei:
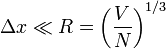
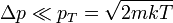
Ezeket behelyettesítve a határozatlansági relációba és mindkét oldal harmadik hatványát véve pont az előbbi feltételt kapjuk.
Bose-Einstein kondenzáció
A Bose-kondenzáció lényege, hogy a hőmérsékletet csökkentve egy megmaradó számú részecskéből álló Bose-gázban makroszkópikusan sok részecske lesz a legalsó energiaszinten (mivel az egy energiaszinten levő részecskék számát semmi sem korlátozza), a 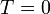 hőmérsékletű határesetet véve az összes részecske a legalsó szinten lenne.
hőmérsékletű határesetet véve az összes részecske a legalsó szinten lenne.
Legyen egy dobozba zárt ideális Bose-gázunk (ahol a részecskék száma megmarad), és kezdjük el hűteni. Mivel a részecskék száma megmarad, a sűrűségnek is állandónak kell lennie. A sűrűség:
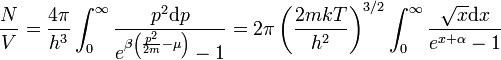
Itt felhasználtuk a 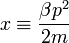 és a
és a 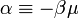 helyettesítéseket. Mivel itt a legalsó energiaszintet 0-nak vettük, így
helyettesítéseket. Mivel itt a legalsó energiaszintet 0-nak vettük, így 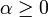 . Az integrál szorzója egy véges szám, ami a hőmérsékletet csökkentve egyre csökken, így ahhoz, hogy a sűrűség állandó maradjon, az integrál értékének nőnie kell. Az integrál az
. Az integrál szorzója egy véges szám, ami a hőmérsékletet csökkentve egyre csökken, így ahhoz, hogy a sűrűség állandó maradjon, az integrál értékének nőnie kell. Az integrál az 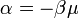 paraméter függvénye, így az integrál növekedése a kémiai potenciál változtatásával érhető el. Megvizsgálva az integrál eredményéül adódó függvényt azt kapjuk, hogy az
paraméter függvénye, így az integrál növekedése a kémiai potenciál változtatásával érhető el. Megvizsgálva az integrál eredményéül adódó függvényt azt kapjuk, hogy az 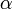 -nak a monoton csökkenő függvénye, és
-nak a monoton csökkenő függvénye, és 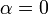 -nál is véges értéket vesz fel.
-nál is véges értéket vesz fel.
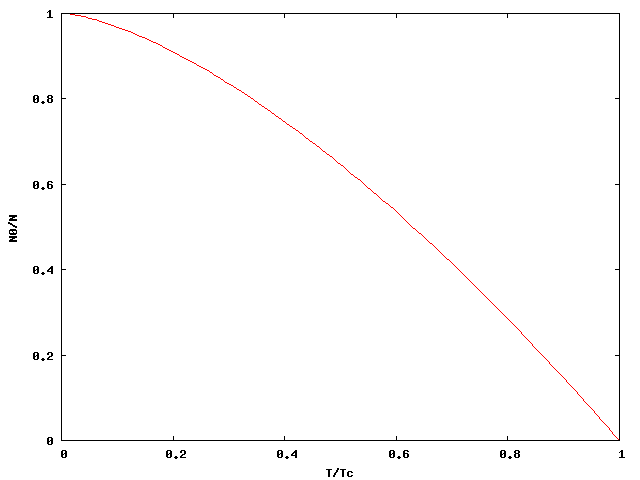
Mivel az integrál előtti szorzó tetszőlegesen kis értéket felvehet a hőmérsékletet csökkentve, ezért az integrál értékének növekedése ezt csak egy ideig tudja kompenzálni, egy kritikus hőmérséklet alatt (ahol 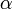 eléri a 0-t) a részecskeszám elkezd csökkenni, és a hőmérséklettel 0-hoz tartva az integrállal számolt részecskeszám is 0-hoz tart, ami ellentmond annak a feltevésnek, hogy a rendszerben a részecskék száma megmarad.
eléri a 0-t) a részecskeszám elkezd csökkenni, és a hőmérséklettel 0-hoz tartva az integrállal számolt részecskeszám is 0-hoz tart, ami ellentmond annak a feltevésnek, hogy a rendszerben a részecskék száma megmarad.
Az ellentmondás abból fakad, hogy a részecskeszám integrállal kiszámítása csak egy közelítés, a valóságban diszkrét állapotok vannak, és ezekre összegzést kell végezni. A legalacsonyabb energiaszinten levő részecskék száma:
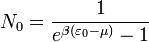
A fenti esetben 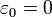 és így az exponenciális függvény kitevőjében pont
és így az exponenciális függvény kitevőjében pont 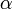 áll. Abban az esetben, ha
áll. Abban az esetben, ha 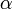 0-hoz tart (azaz a kémiai potenciál tart a legalacsonyabb energiájú állapothoz),
0-hoz tart (azaz a kémiai potenciál tart a legalacsonyabb energiájú állapothoz), 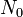 értéke divergál, a legalacsonyabb állapotban levő részecskék száma akármilyen nagy lehet. Az első gerjesztett állapotban levő részecskék száma már véges, nagyságrendekkel kisebb lesz, így az a többi állapottal együtt integrállal kezelhető. Így a részecskeszám kiszámításához a kritikus hőmérséklet alatt a legalsó energiaszinten levő részecskék számát külön kell venni, a többi részecskét lehet integrállal számolni (
értéke divergál, a legalacsonyabb állapotban levő részecskék száma akármilyen nagy lehet. Az első gerjesztett állapotban levő részecskék száma már véges, nagyságrendekkel kisebb lesz, így az a többi állapottal együtt integrállal kezelhető. Így a részecskeszám kiszámításához a kritikus hőmérséklet alatt a legalsó energiaszinten levő részecskék számát külön kell venni, a többi részecskét lehet integrállal számolni (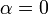 -val számolva). A részecskék száma a kritikus hőmérsékleten:
-val számolva). A részecskék száma a kritikus hőmérsékleten:
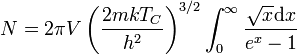
A kritikus hőmérséklet alatt:
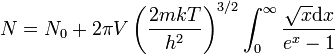
Itt 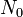 adja a legalsó szinten levő részecskék számát, az integrálos tag pedig a magasabb energiaszinteken levő részecskéket. Ha a gáz hűtése közben a részecskék száma megmarad, akkor a két részecskeszám megegyezik és ebből
adja a legalsó szinten levő részecskék számát, az integrálos tag pedig a magasabb energiaszinteken levő részecskéket. Ha a gáz hűtése közben a részecskék száma megmarad, akkor a két részecskeszám megegyezik és ebből 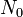 kifejezhető:
kifejezhető:
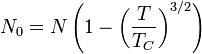
A természetben ritka alkáli gőzökben (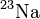 és
és 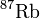 ) figyeltek meg Bose-kondenzációt, pár
) figyeltek meg Bose-kondenzációt, pár 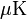 hőmérsékleten, mágneses csapdákban lehűtve. Az elsőre szóba jövő jelölt
hőmérsékleten, mágneses csapdákban lehűtve. Az elsőre szóba jövő jelölt 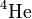 -nél azon a hőmérsékleten és sűrűségen, ahol Bose-kondenzációra lehetne számítani, már folyadék halmazállapotba kerül, ahol már nem elhanyagolható a részecskék közötti kölcsönhatás, a Bose-kondenzáció helyett a szuperfolyékonyság jelenik meg, ami szintén egy makroszkópikus kvantumeffektus.
-nél azon a hőmérsékleten és sűrűségen, ahol Bose-kondenzációra lehetne számítani, már folyadék halmazállapotba kerül, ahol már nem elhanyagolható a részecskék közötti kölcsönhatás, a Bose-kondenzáció helyett a szuperfolyékonyság jelenik meg, ami szintén egy makroszkópikus kvantumeffektus.
Hőmérsékleti sugárzás, Stefan-Boltzmann törvény
Vizsgáljuk meg egy (az egyszerűség kedvéért kocka alakú) kályhában kialakuló sugárzást! A kályha falait tökéletesen tükrözőnek (tökéletes vezető fémnek) feltételezve a Maxwell-egyenletek megoldásaként adódó állóhullámok felelnek meg a rendszer energiasajátállapotainak. A kályhában véges sok állóhullám módus alakulhat ki, egy módus frekvenciája:
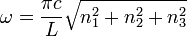
Itt 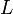 a kocka élhossza,
a kocka élhossza,  a fénysebesség (a hullámok terjedési sebessége),
a fénysebesség (a hullámok terjedési sebessége), 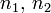 és
és 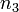 egész számok. Klasszikusan egy módus energiája bármennyi lehetne. A kvantumos tárgyalásban viszont az
egész számok. Klasszikusan egy módus energiája bármennyi lehetne. A kvantumos tárgyalásban viszont az 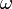 frekvenciájú módus energiája
frekvenciájú módus energiája 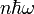 , ahol
, ahol 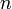 egész szám. Így a rendszer 0 tömegű,
egész szám. Így a rendszer 0 tömegű, 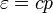 egyrészecske energiájú bozonokként kezelhető, melyekből egy módusban akárhány lehet. Ezeket a részecskéket nevezzük fotonoknak. A fotonokra nincsen részecskeszám megmaradást megkövetelő törvény, így a kémiai potenciáljuk 0, számukat csak a hőmérséklet határozza meg. A rendszer energiája:
egyrészecske energiájú bozonokként kezelhető, melyekből egy módusban akárhány lehet. Ezeket a részecskéket nevezzük fotonoknak. A fotonokra nincsen részecskeszám megmaradást megkövetelő törvény, így a kémiai potenciáljuk 0, számukat csak a hőmérséklet határozza meg. A rendszer energiája:
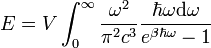
Az integrálban az első tag az 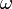 és
és 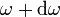 közötti módusok száma, a második tag az Bose-eloszlás az oszcillátor energiájával súlyozva. Az
közötti módusok száma, a második tag az Bose-eloszlás az oszcillátor energiájával súlyozva. Az 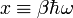 helyettesítéssel az integrálból a hőmérséklet kiemelhető, és az integrál a hőmérséklettől függetlenül elvégezhető, az eredményül adódó energiasűrűség:
helyettesítéssel az integrálból a hőmérséklet kiemelhető, és az integrál a hőmérséklettől függetlenül elvégezhető, az eredményül adódó energiasűrűség:
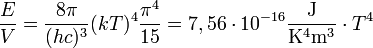
Ez a Stefan-Boltzmann törvény. A fotongáz nyomása:
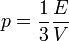
Ez az 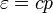 diszperziós reláció következménye, fermionokra is fennálna, a szabadenergia felírásával és parciális integrálással történő átalakításával könnyen belátható.
diszperziós reláció következménye, fermionokra is fennálna, a szabadenergia felírásával és parciális integrálással történő átalakításával könnyen belátható.
Fononok, szilárdtestfizikai alkalmazások (diszperziós reláció)
Első közelítésben a szilárd testek rezgései is szabad Bose-gázként kezelhetőek. Az atomok kis rezgéseinek sajátértékproblémáját (például az atomokat rugókkal összekötött golyóknak képzelve, és lineáris közelítéssel számolva) megoldva a foton problémához hasonlóan állóhullám módusokat kapunk, fontos különbség az, hogy itt a hullámhossz nem lehet a rácsállandónál kisebb, így véges sok módust kapunk (szemben azzal, hogy a hőmérsékleti sugárzás hullámhossza tetszőlegesen kicsi lehet). Feltételezve, hogy egy módus energiája 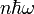 lehet, ahol
lehet, ahol 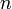 egész szám, az atomok rezgéseit kvázirészecskékkel lehet helettesíteni, amiket fononoknak nevezünk. A számítás a fotonokéhoz hasonló, fontos különbség, hogy az állapotsűrűség kifejezése más (bonyolultabb) és az, hogy csak véges sok módust kell összeadni.
egész szám, az atomok rezgéseit kvázirészecskékkel lehet helettesíteni, amiket fononoknak nevezünk. A számítás a fotonokéhoz hasonló, fontos különbség, hogy az állapotsűrűség kifejezése más (bonyolultabb) és az, hogy csak véges sok módust kell összeadni.
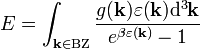
A fenti integrálban a 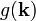 függvény az állapotsűrűség és
függvény az állapotsűrűség és 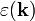 a módus energiája. Ezek általános esetben függhetnek a
a módus energiája. Ezek általános esetben függhetnek a 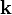 hullámszámvektor irányától is.
hullámszámvektor irányától is.
Egy szilárd testre az 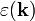 diszperziós reláció általában valamilyen bonyolult függvény, de kis frekvenciákon általában lineáris közelítéssel lehet élni. Alacsony hőmérsékleten csak a kis energiájú módusok gerjesztődnek, így az egész spektrumot vehetjük jó közelítéssel lineárisnak, mert ahol ez már nem teljesülne, azok a módusok már nem (vagy elhanyagolhatóan keveset gerjesztődnek). A diszperziós relációnak általában több ága van, az origóból induló 3 akusztikus ág mellett létezik egy optikai ág is, amiben a 0 hullámszámhoz is véges frekvencia tartozik. A Bruillen-zóna szélénél az optikai és akusztikus ágak találkoznak. Az ehhez tartozó frekvenciára tehetünk egy becslést lineáris közelítésben,
diszperziós reláció általában valamilyen bonyolult függvény, de kis frekvenciákon általában lineáris közelítéssel lehet élni. Alacsony hőmérsékleten csak a kis energiájú módusok gerjesztődnek, így az egész spektrumot vehetjük jó közelítéssel lineárisnak, mert ahol ez már nem teljesülne, azok a módusok már nem (vagy elhanyagolhatóan keveset gerjesztődnek). A diszperziós relációnak általában több ága van, az origóból induló 3 akusztikus ág mellett létezik egy optikai ág is, amiben a 0 hullámszámhoz is véges frekvencia tartozik. A Bruillen-zóna szélénél az optikai és akusztikus ágak találkoznak. Az ehhez tartozó frekvenciára tehetünk egy becslést lineáris közelítésben, 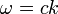 diszperziós relációt feltételezve. A kristályrács rácsállandója
diszperziós relációt feltételezve. A kristályrács rácsállandója 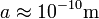 nagyságrendű, a hangsebesség
nagyságrendű, a hangsebesség 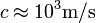 , így a maximális frekvencia
, így a maximális frekvencia 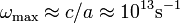 . Az ennek megfelelő hőmérséklet (a Debye-hőmérséklet):
. Az ennek megfelelő hőmérséklet (a Debye-hőmérséklet):
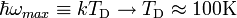
A Debye-hőmérsékletnél jóval alacsonyabb hőmérsékleten úgy tehetünk, mintha az egész spektrum lineáris lenne, és a módusokat a véges 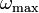 helyett végtelenig számoljuk, mert az
helyett végtelenig számoljuk, mert az 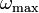 körüli módusok már nem tudnak gerjesztődni, így a számolás teljesen ugyanaz lesz, mint a hőmérsékleti sugárzásnál. Vegyük még figyelembe, hogy a hanghullámoknak két transzverzális és egy longitudinális módusa is lehetséges, amiknek a terjedési sebessége általában különbözik, ennek a kezelésére vezessük be az effektív hangsebességet:
körüli módusok már nem tudnak gerjesztődni, így a számolás teljesen ugyanaz lesz, mint a hőmérsékleti sugárzásnál. Vegyük még figyelembe, hogy a hanghullámoknak két transzverzális és egy longitudinális módusa is lehetséges, amiknek a terjedési sebessége általában különbözik, ennek a kezelésére vezessük be az effektív hangsebességet:
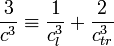 Ezzel a képletek a hőmérsékleti sugárzáshoz hasonlóak lesznek. Az energia és a fajhő:
Ezzel a képletek a hőmérsékleti sugárzáshoz hasonlóak lesznek. Az energia és a fajhő:
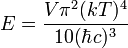
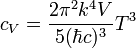
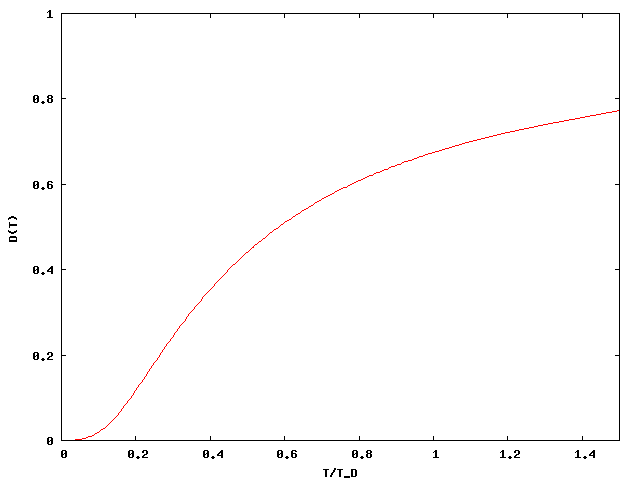
A lineáris spektrumra jellemző, hogy a fajhő a hőmérséklet harmadik hatványától függ, szilárd testeknél alacsony hőmérsékleten a fajhő ezt a viselkedést mutatja. A fenti képletek csak alacsony (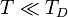 ) hőmérsékleten érvényesek, amíg csak azok a módusok gerjesztődnek, ahol még érvényes az itt alkalmazott közelítés.
) hőmérsékleten érvényesek, amíg csak azok a módusok gerjesztődnek, ahol még érvényes az itt alkalmazott közelítés.
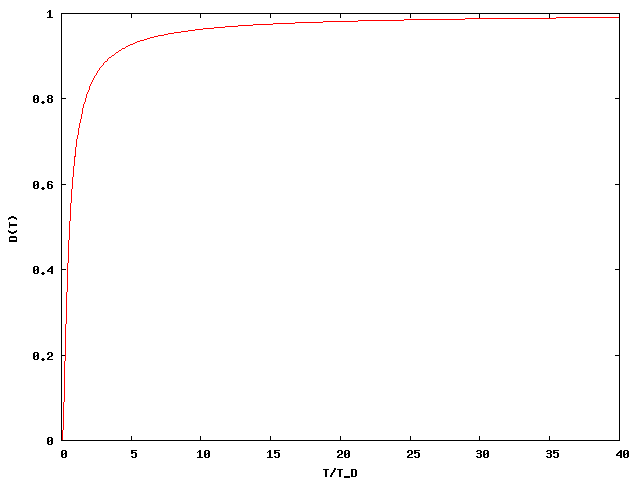
A Debye-hőmérsékletnél jóval magasabb hőmérsékleten már az összes módus gerjesztődik, viszont az összes módusra teljesül, hogy 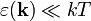 , így a
, így a 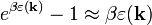 közelítést alkalmazhatjuk, amivel az energia:
közelítést alkalmazhatjuk, amivel az energia:
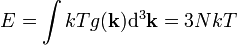 Felhasználtuk, hogy az állapotsűrűség integrálja az összes módus számát adja, így az adódott eredményül, hogy elég magas (sok anyagra már szobahőmérsékletnél) hőmérsékleten teljesül az ekvipartíció, minden módusra
Felhasználtuk, hogy az állapotsűrűség integrálja az összes módus számát adja, így az adódott eredményül, hogy elég magas (sok anyagra már szobahőmérsékletnél) hőmérsékleten teljesül az ekvipartíció, minden módusra 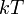 energia jut, a fajhő nem függ a hőmérséklettől.
energia jut, a fajhő nem függ a hőmérséklettől.
A Debye hőmérséklet közelében is elvégezhetünk egy közelítést. Tegyük fel, hogy a spektrum a maximális hullámszámig lineáris, de nem a valódi maximális hullámszámot használjuk, hanem egy olyan effektív értéket, ami biztosítja, hogy a módusok száma megfeleljen a valóságnak:
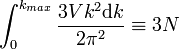
Ezzel felírva az energia:
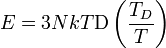
Ebben a magas hőmérsékleten számolt eredmény a Debye-függvénnyel van megszorozva:
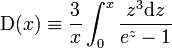
A Debye-függvény alacsony hőmérsékleten a hőmérséklet köbével arányosan indul, magas hőmérsékleten viszont 1-hez tart, ez megfelel a korábban számolt két határesetnek.
Degenerált Fermi-gáz
A 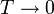 határesetet véve a Fermi-eloszlásfüggvény lépcsőfüggvénybe megy át: a kémiai potenciál alatti állapotok be vannak töltve, a felette levőkben nincs részecske. Így 0 hőmérsékleten az integrálok könnyen elvégezhetőek, ez az alacsony hőmérsékletű Fermi-gázokra jó közelítés lehet. A kémiai potenciált 0 hőmérsékleten Fermi-energiának is nevezik:
határesetet véve a Fermi-eloszlásfüggvény lépcsőfüggvénybe megy át: a kémiai potenciál alatti állapotok be vannak töltve, a felette levőkben nincs részecske. Így 0 hőmérsékleten az integrálok könnyen elvégezhetőek, ez az alacsony hőmérsékletű Fermi-gázokra jó közelítés lehet. A kémiai potenciált 0 hőmérsékleten Fermi-energiának is nevezik: 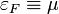 . A részecskeszám számítása:
. A részecskeszám számítása:
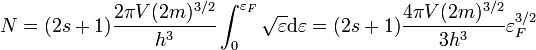
Az energia hasonlóan számolható, az eredmény:
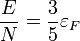
Annak a feltétele, hogy ez a közelítés jó legyen felírható úgy is, hogy a hőmérséklet jóval kisebb legyen a Fermi-energiának megfelelő Fermi-hőmérsékletnél: 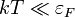 . Fémek vezetési elektronjaira a Fermi-hőmérséklet
. Fémek vezetési elektronjaira a Fermi-hőmérséklet 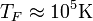 , így ott ez egy elég jó közelítés.
, így ott ez egy elég jó közelítés.
Elektronfajhő, kvantumkorrekciók. {Bethe-Sommerfeld sorfejtés, Landau-paramágnesség}
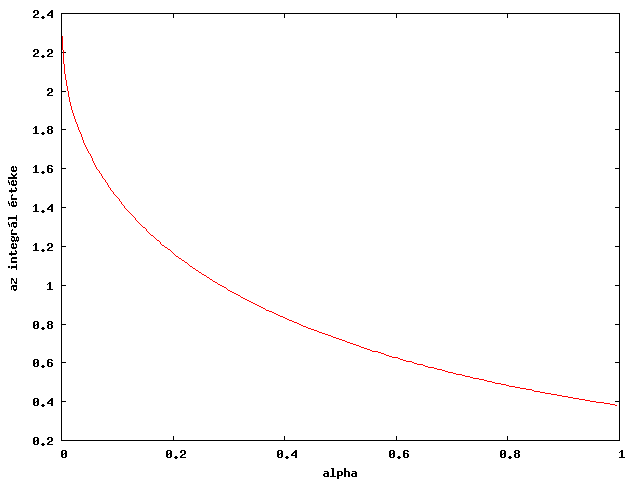
Alacsony hőmérsékletű rendszereknél alkalmazható módszer a Bethe-Sommerfeld sorfejtés, aminek a lényege az, hogy a Fermi-eloszlást tartalmazó integrált 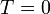 körül sorbafejtjük.
Legyen a kiszámítandó integrál:
körül sorbafejtjük.
Legyen a kiszámítandó integrál:
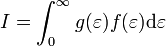
A fenti képletben 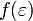 a Fermi-eloszlás és legyen
a Fermi-eloszlás és legyen 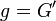 (azaz a
(azaz a 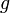 függvény integrálja ismert, ami a 0 hőmérsékletű határesetnek felel meg. Ekkor parciálisan integrálva, majd a
függvény integrálja ismert, ami a 0 hőmérsékletű határesetnek felel meg. Ekkor parciálisan integrálva, majd a 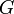 függvény a kémiai potenciál körül sorbafejtve a következőt kapjuk:
függvény a kémiai potenciál körül sorbafejtve a következőt kapjuk:
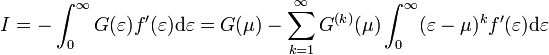
Az első tag a 0 hőmérsékletű határeset, az összegzésben a páratlan tagok 0-t adnak a páros tagokban az integrál elvégezhető, az eredmény:
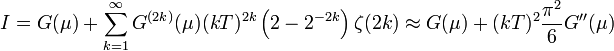
Sokszor elég csak a legelső tagot megtartani, az eredeti jelölésekkel:
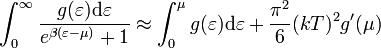
Ezzel például meghatározhatjuk a fémek fajhőjéhez az elektronok által adott járulékát (az elektronokat szabad Fermi-gáznak tekintve). A fémeknél a szobahőmérséklet nagyon kicsi a Fermi-hőmérséklethez képest, így elég csak az első tagot megtartani. Az a hőmérséklet négyzetétől függ, így a belőle számolt fajhőjárulék lineáris lesz. A pontos eredmény:
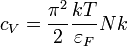
Ez (mivel 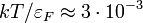 ) szobahőmérsékleten a fononok fajhőjéhez képest elhanyagolhatóan kicsi, viszont a hőmérséklet függvényében változik (a fononokból származó fajhő itt már konstans), ezért ki lehet mérni. Alacsony hőmérsékleten viszont a köbösen induló fononfajhőhöz képest ez adja a nagyobb járulékot.
) szobahőmérsékleten a fononok fajhőjéhez képest elhanyagolhatóan kicsi, viszont a hőmérséklet függvényében változik (a fononokból származó fajhő itt már konstans), ezért ki lehet mérni. Alacsony hőmérsékleten viszont a köbösen induló fononfajhőhöz képest ez adja a nagyobb járulékot.