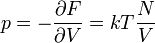A termodinamika statisztikus alapozása
Tartalomjegyzék
- 1 Az egyensúlyi statisztikus fizika feltevései
- 2 A Gibbs féle sokaságfogalom
- 3 Az entrópia
- 4 A mikrokanonikus sokaság
- 5 A hőmérséklet
- 6 A nyomás
- 7 A kémiai potenciál
- 8 Fundamentális egyenlet
- 9 Az első főtétel
- 10 A második főtétel
- 11 A harmadik főtétel
- 12 Kanonikus sokaság
- 13 Az ekvipartíció tétele
- 14 Egyensúly körüli fluktuációk
- 15 A szabadenergia
- 16 Nagykanonikus sokaság
- 17 A nagykanonikus potenciál
- 18 A klasszikus ideális gáz
Az egyensúlyi statisztikus fizika feltevései
I. posztulátum: A magukra hagyott makroszkopikus rendszerek kellően hosszú idő után a termodinamikai egyensúly állapotába kerülnek.
Az egyensúly beállásában fontos a rendszer részrendszerei közötti kölcsönhatás, ha az egyensúly már beállt, akkor viszont a kölcsönhatás az esetek többségében elhanyagolható.
II. posztulátum: Egyensúlyi állapotban lévő rendszer minden olyan mikroállapotát egyenlő valószínűséggel veszi fel, amely a róla szerzett, nem teljes információval (tipikusan makroszkopikus állapotjelzővel) összeegyeztethető. Másképp fogalmazva, ha a rendszerről kevesebb információnk van, mint amennyi az összes mikroállapotot rögzítené, akkor az általunk megfigyelhető állapotot a rendszer egynél több mikroállapottal tudja megvalósítani, és ezeket egyforma valószínűséggel fogja felvenni.
Ez a posztulátum azt jelenti, hogy nem vetítünk a rendszerre olyan információt, amelyet nem tudunk róla. Ez pedig a statisztikus fizika kivételével minden más tudományágra jellemző! A feltétel matematikai megfogalmazása az entrópia maximalizálását jelenti.
A Gibbs féle sokaságfogalom
Egy makroállapothoz nagyon sok különböző mikroállapot tartozik. Ezt úgy mondhatjuk, hogy a makroszkopikus tulajdonságok ismerete nem egy makroszkopikus testet határoz meg, hanem azok egy sokaságát. Ezt a halmazt nevezzük Gibbs féle sokaságnak.
Termodinamikai egyensúlyban lévő rendszerek esetében a rajtuk végzett mérések eredménye független a mérés idejétől, így a mért érték a mennyiség időbeli átlagának tekinthető. A mérés ideje alatt azonban a rendszer sok mikroállapotát megvalósítja, így azt várjuk, hogy a sokaságra vett átlag megegyezik az időbeli átlaggal. Ha ez teljesül, akkor a bonyolult időbeli átlagtól eltekinthetünk.
A sokaság megadása eloszlásfügvénnyel történik. 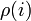 azt adja meg, hogy milyen valószínűséggel van a rendszer az i. állapotában. A normálást a
azt adja meg, hogy milyen valószínűséggel van a rendszer az i. állapotában. A normálást a
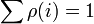
feltétel adja. Egy A fizikai mennyiség sokaságátlaga pedig:
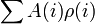
Kvantumos rendszer esetén ez a rendszer állapotaira való szummázást jelenti, azonos részecskékből álló klasszikus fizikai rendszer esetén pedig
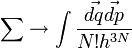
helyettesítés alkalmazandó. Az 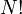 és a
és a 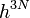 tag szükségességére később talán még visszatérünk. Egyelőre annyit említünk meg, hogy nyilvánvaló módon, egy klasszikus fizikai rendszer végtelen sok állapotban lehet, hiszen folytonos értékeket vesznek fel mind a koordináták, mind az impulzusok. Ahhoz, hogy meg tudjuk számolni az állapotokat, a fázisteret valahogy diszkretizálni kell, például kis hiperkockákra kell bontani. Ha a rendszer egy adott kockában van, az tekinthető egy állapotnak. Dimenzióanalízis adja, hogy a képletben szereplő h-nak hatásdimenziójú mennyiségnek kell lennie. Az, hogy ez ténylegesen a Planck-állandó, pedig a kvantumstatisztikák klasszikus határátmenetének elvégzésekor olvasható le. Az N! szorzó kvantummechanikai esetben szintén természetesnek hat, hiszen az azonos részecskék megkülönböztethetetlenek, azonban a klasszikus fizikában ez nem igaz, ez vezetett a Gibbs-paradoxonhoz, amely lényegében azt jelenti, hogy ahhoz, hogy az entrópia extenzív mennyiség legyen, szükség volt az N! bevezetésére.
tag szükségességére később talán még visszatérünk. Egyelőre annyit említünk meg, hogy nyilvánvaló módon, egy klasszikus fizikai rendszer végtelen sok állapotban lehet, hiszen folytonos értékeket vesznek fel mind a koordináták, mind az impulzusok. Ahhoz, hogy meg tudjuk számolni az állapotokat, a fázisteret valahogy diszkretizálni kell, például kis hiperkockákra kell bontani. Ha a rendszer egy adott kockában van, az tekinthető egy állapotnak. Dimenzióanalízis adja, hogy a képletben szereplő h-nak hatásdimenziójú mennyiségnek kell lennie. Az, hogy ez ténylegesen a Planck-állandó, pedig a kvantumstatisztikák klasszikus határátmenetének elvégzésekor olvasható le. Az N! szorzó kvantummechanikai esetben szintén természetesnek hat, hiszen az azonos részecskék megkülönböztethetetlenek, azonban a klasszikus fizikában ez nem igaz, ez vezetett a Gibbs-paradoxonhoz, amely lényegében azt jelenti, hogy ahhoz, hogy az entrópia extenzív mennyiség legyen, szükség volt az N! bevezetésére.
Az entrópia
Definíció szerint az entrópia:
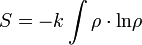
Az entrópia maximalizálása jelenti a II. posztulátum teljesítését. Miért?
Az így definiált entrópia a Shannon féle információelméleti entrópia:
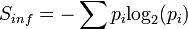 ,
,
ahol 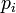 általánosított valószínűségeloszlás. Ennek a következő tulajdonságai vannak:
általánosított valószínűségeloszlás. Ennek a következő tulajdonságai vannak:
- Biztos eseményre minimális.
- Ha
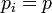 minden i-re, akkor maximális.
minden i-re, akkor maximális. - Független eloszlásokra additív.
Ezek pont azok a tulajdonságok, amiket az entrópiától elvárunk. Tehát mindig az entrópia szélsőértékét kell keresni, a makroszkopikusan adott mennyiségeket mint mellékfeltételt figyelembevéve. Ennek matematikai módszere a variációszámítás alkalmazása az S funkcionálra, a mellékfeltételek pedig Lagrange-multiplikátorok segítségével vehetők figyelembe.
A mikrokanonikus sokaság
A mikrokanonikus sokaság a zárt rendszer statisztikus modellje. Itt az ismert makroszkopikus feltétel az, hogy a rendszer teljes enerigája 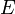 és
és 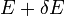 között legyen. Az eloszlásfüggvény:
között legyen. Az eloszlásfüggvény:
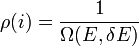 ha
ha 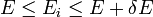 , máshol pedig 0.
, máshol pedig 0.
Ahol mikroállapotok száma:
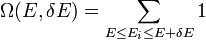
illetve klasszikus esetben
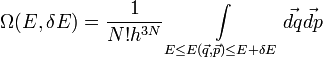
Itt hallgatólagosan kihasználtuk, hogy a fázistérbeli sűrűség csak az energiától függ. Ennek hátterében az áll, hogy stacionárius megoldást keresünk(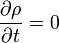 ). Ebből a Liouville-egyenlet szerint következik, hogy a fázistérbeli sűrűség csak additív mozgásállandóktól függhet. Megfelelő koordinátarendszert választva az impulzus és az impulzusmomentum 0, így a fázistérbeli sűrűség valóban csak az energiától függ. Ez a hatalmas redukció a paraméterek számában(
). Ebből a Liouville-egyenlet szerint következik, hogy a fázistérbeli sűrűség csak additív mozgásállandóktól függhet. Megfelelő koordinátarendszert választva az impulzus és az impulzusmomentum 0, így a fázistérbeli sűrűség valóban csak az energiától függ. Ez a hatalmas redukció a paraméterek számában(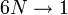 ) a statisztikus fizika egyik legfontosabb elméleti pillére.
) a statisztikus fizika egyik legfontosabb elméleti pillére.
Az eloszlásfüggvényt behelyettesítve az entrópia definíciójába megkapjuk az eredeti Gibbs féle entrópiafogalmat, amely zárt rendszerre érvényes:
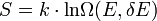
Innen még úgy tűnhet, hogy az entrópia még függ a kis 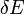 megválasztásától is, ez azonban nagyon jó közelítéssel nem igaz, sőt, gyakorlati alkalmazásokban
megválasztásától is, ez azonban nagyon jó közelítéssel nem igaz, sőt, gyakorlati alkalmazásokban 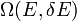 helyettesíthető:
helyettesíthető:
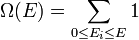 -el
-el
illetve klasszikus esetben a:
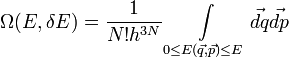
függvénnyel.
Az S természetes változói az extenzív állapotjelzők: S(E,V,N).
Ha x egy fizikai mennyiség, akkor annak a valószínűsége, hogy egy 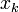 értéket vesz fel
értéket vesz fel
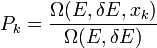
ahol 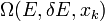 azon állapotok száma, amelyek az energia
azon állapotok száma, amelyek az energia 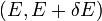 közötti értéke mellett még rögzített
közötti értéke mellett még rögzített 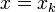 értékkel is rendelkeznek.
értékkel is rendelkeznek.
A hőmérséklet
Tekintsünk egy zárt rendszert, amely két alrendszerből áll, melyek között energia áramolhat. Ekkor az összes állapotok száma egyenlő a részrendszerek állapotszámainak szorzatával:
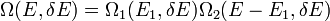
Ekkor az egyensúly feltétele (az entrópia szélsőértéke: 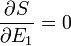 ) a következőhöz vezet
) a következőhöz vezet
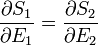
mivel tudjuk, hogy az egyensúlyi feltétel a fenomenologikus termodinamikában a hőmérsékletek egyenlősége, ezért dimenzióanalízissel adódik, hogy a T hőmérsékletet érdemes a következőképpen definiálni:
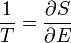
Később majd látjuk, hogy ez valóban ugyanaz, mint a termodinamikai hőmérséklet.
A nyomás
Tekintsünk egy olyan zárt rendszert, melynek egyik alrendszere 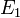 energiájú,
energiájú, 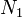 részecskét tartalmazó gáz, a másik alrendszere pedig egy
részecskét tartalmazó gáz, a másik alrendszere pedig egy 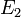 energiájú rugó, a két alrendszert dugattyú választja el. Itt ismételten keresve az entrópia szélsőértékét, a mechanikai egyensúly feltételével (erők egyenlősége) összeegyeztethető egyenlőséget kapunk, ha a gáz p nyomását a következőképpen definiáljuk:
energiájú rugó, a két alrendszert dugattyú választja el. Itt ismételten keresve az entrópia szélsőértékét, a mechanikai egyensúly feltételével (erők egyenlősége) összeegyeztethető egyenlőséget kapunk, ha a gáz p nyomását a következőképpen definiáljuk:
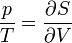
A kémiai potenciál
Ha egy olyan rendszert tekintünk, melyek két alrendszere részecske és energiacserére képes, térfogata viszont állandó. Ekkor szintéén kapunk egy egyensúlyi feltételt, amely a kémiai potenciálok kiegyenlítődését adja, ha a kémiai potenciál a következőkppen definiáljuk:
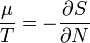
Fundamentális egyenlet
Az előző három pontban leírtak szerint az entrópia teljes differenciálja:
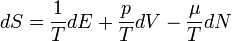
ennek átrendezése adja a fundamentális egyenletet:
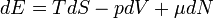
Az első főtétel
Legyen egyelőre a részecskeszám állandó. Hasonlítsuk össze a termodinamika első főtételét a fundamentális egyenlettel! Az első szerint:
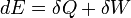
a második szerint:
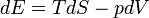
Vonzó ötlet a két egyenlet egyes tagjait azonosítani, de ez a legáltalánosabb esetben nem helyes. Persze a bal oldalak azonos kezdő- és végállapotok esetén egyenlőek. Az első egyenlet az energiamegmaradást fejezi ki, a test energiájának megváltozása egyenlő a munka és a hőközlés összegével. A második egyenlet csak egyensúlyban értelmezhető, hiszen T és p egyébként nem értelmes mennyiségek, tehát ez az egyenlet csak két egyensúlyi állapot energiakülönbségéről szól. De általánosan nem igaz, hogy 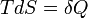 . Például tekintsünk egy olyan zárt rendszert, amely egy V,T,p állapotjelzőkkel leírható gáztól egy elválasztóval elválasztott dV térfogatú vákuumot tartalmaz még. Ekkor ha a válaszfalat a felület normálisára merőleges irányban kirántjuk, akkor
. Például tekintsünk egy olyan zárt rendszert, amely egy V,T,p állapotjelzőkkel leírható gáztól egy elválasztóval elválasztott dV térfogatú vákuumot tartalmaz még. Ekkor ha a válaszfalat a felület normálisára merőleges irányban kirántjuk, akkor 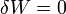 , hiszen merőleges az elmozdulás és az erő. Ugyanakkor a rendszert zárt, tehát
, hiszen merőleges az elmozdulás és az erő. Ugyanakkor a rendszert zárt, tehát 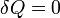 . Ekkor dE=0. Ugyanakkor pdV nem 0, és TdS=pdV. Ezért
. Ekkor dE=0. Ugyanakkor pdV nem 0, és TdS=pdV. Ezért 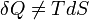 . Ugyanakkor, ha a folyamat olyan lassan megy végbe, hogy a változás közben a rendszert pillanatnyi paramétereivel jellemzett egyensúlyi állapotban lévőnek vehetjük (kvázisztatikus folyamat), akkor az egyenlet két tagja valóban egyenlő, hiszen térfogati munkát tekintve:
. Ugyanakkor, ha a folyamat olyan lassan megy végbe, hogy a változás közben a rendszert pillanatnyi paramétereivel jellemzett egyensúlyi állapotban lévőnek vehetjük (kvázisztatikus folyamat), akkor az egyenlet két tagja valóban egyenlő, hiszen térfogati munkát tekintve:
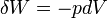
Ebből következik, hogy:
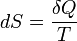
Beláttuk, hogy a termodinamikai és a statisztikus fizikai entrópia fogalom ekvivalens.
A második főtétel
A második főtétel szerint spontán folyamatokban az entrópia mindig nő. Ez az állítás következik az 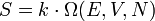 definícióból, ugyanis spontán változásokban az állapotok száma mindig nő. Például, ha egy hőszigetelt edényt válaszfallal két részre bontunk, és az egyik felében gáz van, a másikban vákuum, akkor a válaszfal elhúzása után a gáz kitölti az egész edényt, megvan minden korábbi állapota, de nagyon sok más is, így az entrópia nő.
definícióból, ugyanis spontán változásokban az állapotok száma mindig nő. Például, ha egy hőszigetelt edényt válaszfallal két részre bontunk, és az egyik felében gáz van, a másikban vákuum, akkor a válaszfal elhúzása után a gáz kitölti az egész edényt, megvan minden korábbi állapota, de nagyon sok más is, így az entrópia nő.
Nem zárt rendszer esetén a második főtétel:
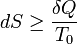
ez is könnyen belátható, ha az A rendszerből és az A' tartályból álló zárt rendszert tekintjük, a tartály ugyanis nagy, benne a változás kvázisztatikus ezért entrópiváltozása 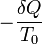 , a teljes rendszerre pedig igaz a zárt rendszerre vonatkozó főtétel.
, a teljes rendszerre pedig igaz a zárt rendszerre vonatkozó főtétel.
A harmadik főtétel
A harmadik főtétel azt mondja ki, hogy 0 hőmérséklethez tartava az entrópia is 0-hoz tart. Ez nem igazolható általánosan, csak a konkrét rendszer tulajdonságait figyelembe véve.
Kanonikus sokaság
A kanonikus sokaság a hőtartályban lévő test statisztikus modellje. A szokásos normálási feltétel mellett adott az energia várhatóértéke:
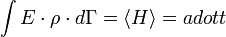
A Lagrange multiplikátor módszerrel ezt a kényszert figyelembe véve az eloszlásfüggvényre a következő adódik:
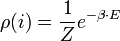
ahol 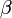 mint Lagrange-multiplikátor jelent meg, ahol az állapotösszeg:
mint Lagrange-multiplikátor jelent meg, ahol az állapotösszeg:
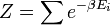 ,
,
illetve N klasszikus részecske esetén:
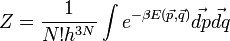
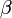 dimenzióanalízis miatt energia mértékegységű. Hogy pontosan micsoda, az a következőképpen dönthető el. Tekintsünk egy zárt rendszert, amely áll a kérdéses kanonikus rendszerből és a hőtartályból. A kettő együtt a mikrokanonikus sokasággal írható le, a rendszer összenergiája E. Ekkor annak a valószínűsége, hogy a kis méretű rendszer energiája
dimenzióanalízis miatt energia mértékegységű. Hogy pontosan micsoda, az a következőképpen dönthető el. Tekintsünk egy zárt rendszert, amely áll a kérdéses kanonikus rendszerből és a hőtartályból. A kettő együtt a mikrokanonikus sokasággal írható le, a rendszer összenergiája E. Ekkor annak a valószínűsége, hogy a kis méretű rendszer energiája 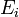 :
:
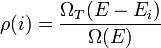
ahol T a hőtartályt jelenti. Feltételünk szerint 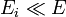 , vagyis ha
, vagyis ha 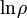 -t sorbafejtjük, akkor:
-t sorbafejtjük, akkor:
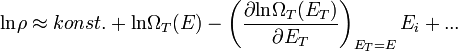
Innen már leolvasható, hogy
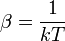 .
.
Az ekvipartíció tétele
Ha egy klasszikus rendszer Hamilton operátor 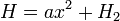 alakú, ahol
alakú, ahol 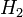 nem függ x-től (ami tetszőleges impulzus vagy koordinátakomponens), akkor
nem függ x-től (ami tetszőleges impulzus vagy koordinátakomponens), akkor
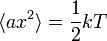 , azaz a Hamilton ezen részére átlagosan
, azaz a Hamilton ezen részére átlagosan 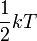 energia jut. Ez az ekvipartíció tétele. A kanonikus formalizmus alapképleteit használva könnyen belátható.
energia jut. Ez az ekvipartíció tétele. A kanonikus formalizmus alapképleteit használva könnyen belátható.
Az ekvipartíciótétel sok egyszerű eredményt ad, ilyen pl.:
Egyatomos ideális gáz energiája:
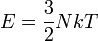
Dulong-Petit szabály: Eredetileg empirikus összefüggés a szilárdtestek hőkapacitásáról. Akkor kapható meg, ha feltételezzük, hogy a szilárd test N független 3 dimenziós oszcillátorból áll. Ekkor
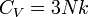 .
.
Egyensúly körüli fluktuációk
Az energia várható értéke:
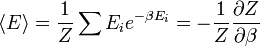
hasonlóan
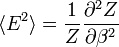
Az energiafluktuációk négyzete:
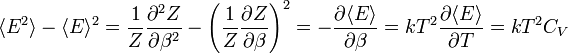
Kihasználva, hogy a hőkapacitás és az energia extenzív mennyiségek révén arányosak N-el relatív fluktuációk:
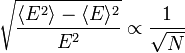
ami, mivel N nagyon nagy szám (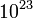 ) arra utal, hogy a fluktuációk makroszkopikus testek esetén nagyon kicsik. Kérdéses azonban, hogy mekkora az arányossági tényező, ez ugyanis fázisátalakulások közelében nagyon megnőhet.
) arra utal, hogy a fluktuációk makroszkopikus testek esetén nagyon kicsik. Kérdéses azonban, hogy mekkora az arányossági tényező, ez ugyanis fázisátalakulások közelében nagyon megnőhet.
A szabadenergia
Ha E energiához 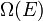 állapot tartozik, akkor az állapotösszeg:
állapot tartozik, akkor az állapotösszeg:
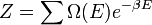
a termodinamikai limitben az energiaeloszlás Dirac-delta szerű, ezért
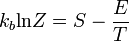
innen a szabadenergia termodinamikai definícióját felhasználva:
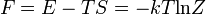
A szabadenergia szemléletesen egy zárt rendszerból kinyerhető hasznos munkát méri állandó hőmérsékleten és nyomáson.
Annak a valószínűsége, hogy egy x extenzív mennyiség értéke x legyen:
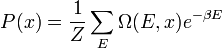
kihasználva, hogy a makroszkopikus testek esetén E eloszlása nagyon keskeny a szummát egyszerűen a legvalószínűbb értékkel helyettesíthetjük:
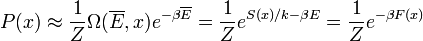
vagyis az egyensúly (a legvalószínűbb állapot) feltétele F minimuma.
Nagykanonikus sokaság
Ha a kis rendszer a nagy rendszertől nem csak hőt vehet át, hanem a részecskék is "átmehetnek a falon", akkor nagykanonikus sokaságról beszélünk, ekkor az energia és a részecskeszám átlagértékét tekintjük adottnak:
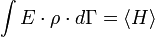
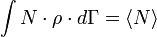
A Lagrange-multiplikátor módszer szerint az eloszlásfüggvény:
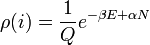
ahol 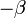 ,
, 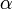 a különböző mellékfeltételekhez tartozó Lagrange-multiplikátorok. A kanonikus eloszlásnál leírthoz hasonló elemzés szerint pedig
a különböző mellékfeltételekhez tartozó Lagrange-multiplikátorok. A kanonikus eloszlásnál leírthoz hasonló elemzés szerint pedig
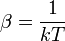
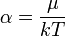
a normáláshoz szükséges Q tényező pedig:
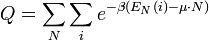
illetve a klasszikus esetben:
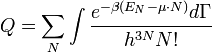
A nagykanonikus potenciál
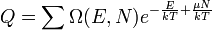
termodinamikai határesetben az eloszlások élesek:
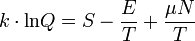
a nagykanonikus potenciál termodinamikai definícióját használva:
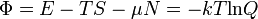
A nagykanonikus potenciál (vagy Landau-potenciál) minimuma lesz az egyensúly feltétele nagykanonikus sokaság esetében. Ez a szabadenergiánál leírthoz hasonló gondolatmenettel belátható. Kémiai egyensúlyban tehát 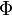 minimális.
minimális.
A klasszikus ideális gáz
Az eddigiek alkalmazásaként lássuk a klasszikus részecskékből álló nem kölcsönható gáz példáját.
Bernoulli-formula(*)
Tekintsünk egy nagyon egyszerű modellt. Egy valamilyen edényben lévő klasszikus ideális gáz esetén, feltéve, hogy erő csak a fallal való ütközéskor lép fel, a viriál:
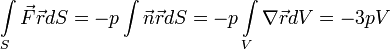
Továbbá:
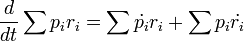
egyenlet időátlagolásával:
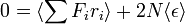
ahol  egy részecske energiája. A két egyenlet összeolvasásával
egy részecske energiája. A két egyenlet összeolvasásával
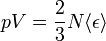
Maxwell gondolatmenete
Maxwell gyakorlatilag még a statisztius fizika megszületése előtt levezette az ideális gáz sebességeloszlását. Annak a valószínűsége, hogy egy atom sebessége 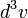 -be esik:
-be esik:
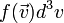
Maxwell gondolatmenete a következő volt:
- Nincs kitüntetett irány
vagyis 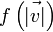 szerint függ, vagyis f-nek v szerinti gradiense párhuzamos v-vel:
szerint függ, vagyis f-nek v szerinti gradiense párhuzamos v-vel:
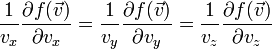
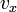 ,
,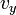 ,
,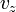 független
független
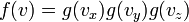
ezért:
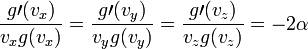
Ennek a differenciálegyenletnek a megoldása:
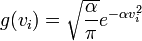
ahol már g normáltságát is kihasználtuk. 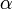 értékét megkaphatnánk az ekvipartíció felhasználásával, hiszen
értékét megkaphatnánk az ekvipartíció felhasználásával, hiszen 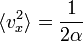 , de ez Maxwell idejében még általánosan nem volt ismert. Helyette a Bernoulli-formula és az ideális gáz állapotegyenletének kombinálásával jutott arra a következtetésre, hogy
, de ez Maxwell idejében még általánosan nem volt ismert. Helyette a Bernoulli-formula és az ideális gáz állapotegyenletének kombinálásával jutott arra a következtetésre, hogy 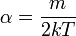 . A sebesség abszolút értéke szerinti eloszlás:
. A sebesség abszolút értéke szerinti eloszlás:
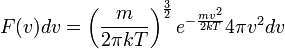
Kanonikus sokaságban
Természetesen a kanonikus sokaság ismeretében a sebességeloszlás rögtön leolvasható az alapképletből. Több is megtehető azonban. Megkapható ugyanis az ideális gáz állapotegyenlete. Az állapotösszeg 3N Gauss-integrál kiszámítása után:
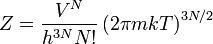
A szabadenergia:
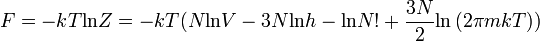
A nyomás: