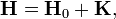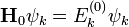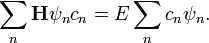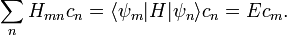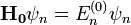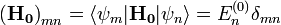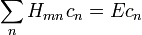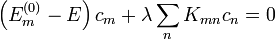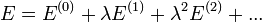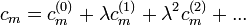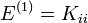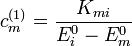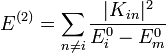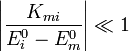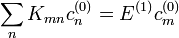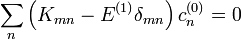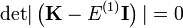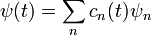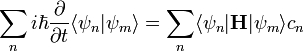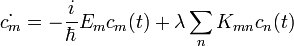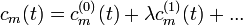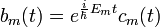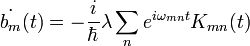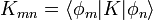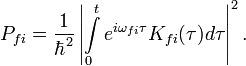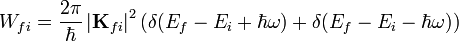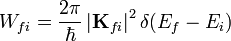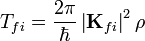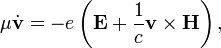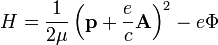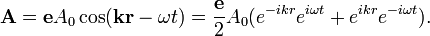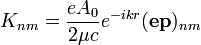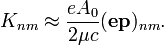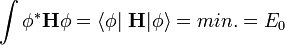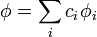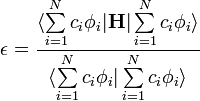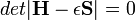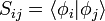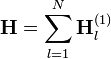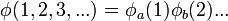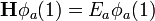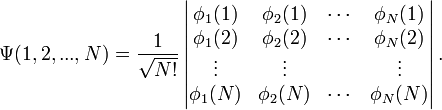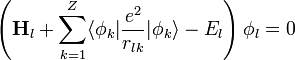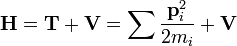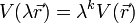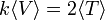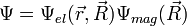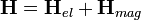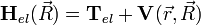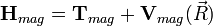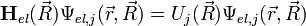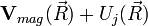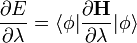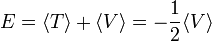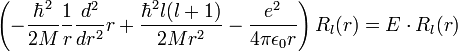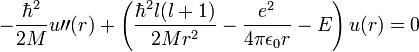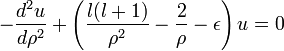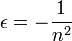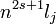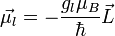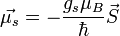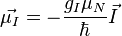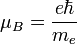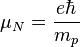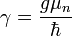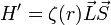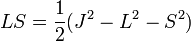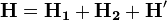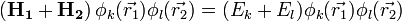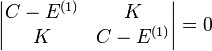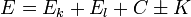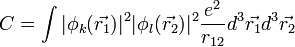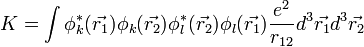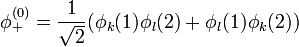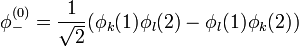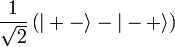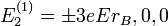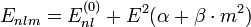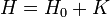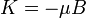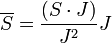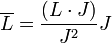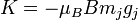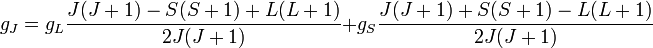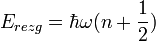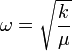Atom- és molekulaszerkezet
Tartalomjegyzék
- 1 Perturbációszámítás[1]
- 2 Variációs módszer
- 3 Problémák a kvantummechanika közelítő módszereivel
- 4 Azonos részecskék, Pauli-elv
- 5 Átlagtérközelítés
- 6 A periódusos rendszer
- 7 Viriál-tétel(*)
- 8 A Born-Oppenheimer közelítés
- 9 Hellmann-Feynman tétel (*)
- 10 A kémiai kötés
- 11 A hidrogén atom
- 12 Atomi energianívók termjelölése
- 13 Mágneses momentumok
- 14 Finomfelhasadás
- 15 Hiperfinom felhasadás
- 16 Lamb shift
- 17 A hélium atom
- 18 Stark-effektus
- 19 Zeeman-effektus
- 20 A molekulaion, kicserélődési kölcsönhatás(*)
- 21 Kétatomos molekulák
- 22 Molekulák rezgési és forgási spektruma
- 23 Alagút-effektus
Perturbációszámítás[1]
A kvantummechanikában előbukkanó problémák általánosságban nem oldhatóak meg egzaktul. Gyakran azonban azt akarjuk meghatározni, hogy egy ismert sajátfüggvényekkel rendelkező rendszert hogy befolyásol egy vele bizonyos értelemben gyengén kölcsönható külső rendszer. Ekkor a vizsgált rendszer Hamilton-operátora csak kicsit különbözik az egzaktul megoldható probléma Hamilton-operátorától:
ahol 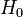 az egzaktul megoldható probléma Hamilton-operátora, és K kicsi
az egzaktul megoldható probléma Hamilton-operátora, és K kicsi 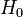 -hoz képest (egy operátor akkor tekinthető kicsinek, ha sajátértékei jóval kisebbek a másikénál).
-hoz képest (egy operátor akkor tekinthető kicsinek, ha sajátértékei jóval kisebbek a másikénál).
Azt várjuk, hogy perturbált probléma megoldása csak kicsit fog különbözni az eredeti probléma egzakt megoldásaitól. Az ilyen alakú problémák ezen megoldási módszerét perturbációszámításnak nevezzük.
Időfüggetlen, nem-degenerált eset
Ebben az esetben azokat a problémákat vizsgáljuk, amikor K időfüggetlen és a perturbálatlan probléma Hamilton-operátora nem elfajult, azaz minden sajátértékhez egyetlen sajátfüggvény tartozik. Feltesszük, hogy a perturbálatlan esethez ismerjük a megoldásokat, és a fentiek ismeretében keressük a perturbált megoldásokat:
Rayleigh-től eredő trükk a perturbáló operátor kicsinységének figyelembevételére az, hogy egy kis 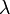 paraméter szerint fejtünk sorba, amely majd később kapja vissza a
paraméter szerint fejtünk sorba, amely majd később kapja vissza a 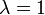 értéket:
értéket:
Ezt a trükköt azért alkalmazzuk, mert az operátor kicsiségét nehéz definiálni. Ezzel a trükkel lényegében azt mondjuk, hogy K legyen egy tetszőleges operátor, melyet megszorzunk egy λ dimenziótlan paraméterrel, melynek értékével nullába tartunk. Ebben az esetben az operátor határesetben garantáltan kicsivé válik, és sorfejtést is tudunk végezni a dimenziótlan λ paraméter szerint. A megoldás végén λ-t egységnyinek tekintjük, hiszen a perturbáló operátor kicsisége magában a perturbáló operátorban kell megjelennie, nincs szükség dimenziótlan paraméterrel való szorzásra, az csak a probléma kezelését könnyíti meg (pl. a sorfejtésnél).
A Schrödinger-egyenletet egy tetszőleges ortogonális bázis segítségével átírhatjuk mátrixos alakba. A probléma összes sajátállapotát természetesen csak akkor kapjuk meg, ha a felhasznált bázis teljes. A bázisnak a perturbálatlan Hamilton-operátor ortogonális sajátfüggvényeit fogjuk használni:
A hullámfüggvényt a bázisfüggvények lineárkombinációjaként keressük 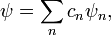 és ezt helyettesítjük be a Schrödinger egyenletbe. Formálisan tehát:
és ezt helyettesítjük be a Schrödinger egyenletbe. Formálisan tehát:
Skalárisan beszorozva mindkét oldalt 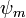 -mel, és felhasználva, hogy
-mel, és felhasználva, hogy 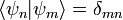 a következőhöz jutunk:
a következőhöz jutunk:
Ez a Schrödinger-egyenlet mátrixalakja. Ezt kívánjuk most megoldani a perturbációszámítás segítségével.
A megoldandó sajátérték-egyenlet tehát 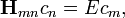 ahol
ahol 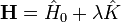 A
A 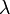 -ban nulladrendet az ismert perturbálatlan megoldás adja. Hamarosan belátjuk, hogy nulladrendben a perturbált probléma sajátenergiái a perturbálatlan probléma sajátenergiáival egyeznek meg.
-ban nulladrendet az ismert perturbálatlan megoldás adja. Hamarosan belátjuk, hogy nulladrendben a perturbált probléma sajátenergiái a perturbálatlan probléma sajátenergiáival egyeznek meg.
Mivel a 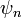 függvények
függvények 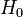 sajátfüggvényei, ezért:
sajátfüggvényei, ezért:
Ezen a bázison a Schrödinger-egyenlet mátrixalakja
A sorfejtések:
Ezt kell beírni az előző Schrödinger-egyenletbe. A különböző tagok együtthatóiról leolvashatók a különböző rendű korrekciók.
A nulladrend ezt adja:
Ennek megoldása 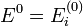 és
és 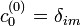 . Ez azt jelenti, hogy nulladrendben a sajátenergiák a perturbálatlan Hamilton-operátorok sajátenergiái, és a sajátfüggvények is megegyeznek a perturbálatlan probléma sajátfüggvényeivel. Ez alapján most már tudjuk egyértelműen indexelni a perturbált probléma keresett sajátállapotait egy i indexszel, mely azt adja meg, hogy nulladrendben melyik perturbálatlan állapotra egyszerűsödik a sajátállapot. Általában ettől az i indextől függeni fognak a λ-ban magasabb rendű korrekciók. A továbbiakban egy tetszőleges i indexű állapotot vizsgálunk.
. Ez azt jelenti, hogy nulladrendben a sajátenergiák a perturbálatlan Hamilton-operátorok sajátenergiái, és a sajátfüggvények is megegyeznek a perturbálatlan probléma sajátfüggvényeivel. Ez alapján most már tudjuk egyértelműen indexelni a perturbált probléma keresett sajátállapotait egy i indexszel, mely azt adja meg, hogy nulladrendben melyik perturbálatlan állapotra egyszerűsödik a sajátállapot. Általában ettől az i indextől függeni fognak a λ-ban magasabb rendű korrekciók. A továbbiakban egy tetszőleges i indexű állapotot vizsgálunk.
Az elsőrendű energiakorrekciók:
Az állapotvektorok elsőrendű korrekciói:
Az energiák másodrendű korrekciói:
A módszer alkalmazható, ha a kiszámol korrekciók tényleg kicsik, vagyis a perturbáció átmeneti mátrixelemei sokkal kisebbek, mint a perturbálatlan energiaszintek különbségei:
Időfüggetlen, degenerált eset
Degenerált esetben egyetlen energiasajátértékhez több sajátfüggvény is tartozhat. A perturbácó hatására ezek az energiaszintek fel is hasadhatnak (gondoljunk a Zeeman-effektusra). Ekkor az előző módszer nem alkalmazható, a 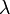 nulladrendjére kapott
nulladrendjére kapott 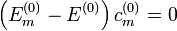 egyenlet nem határozza meg egyértelműen a nulladrendű sajátvektorokat, mert vannak olyan energiasajátértékek, amelyek megegyeznek, és az azokhoz tartozó c-ket nem tudjuk meghatározni. Azt persze továbbra is tudjuk, hogy a más energiájú sajátállapotok együtthatói nulladrendben zérusok. Az azonos energiájú sajátállapotok nulladrendű együtthatóihoz viszont fel kell használni λ-ban a következő rendet is. Ebben megjelenik az energiafelhasadás első rendje is, melyet így szintén megkaphatunk ebből az egyenletből. A kapott egyenlet:
egyenlet nem határozza meg egyértelműen a nulladrendű sajátvektorokat, mert vannak olyan energiasajátértékek, amelyek megegyeznek, és az azokhoz tartozó c-ket nem tudjuk meghatározni. Azt persze továbbra is tudjuk, hogy a más energiájú sajátállapotok együtthatói nulladrendben zérusok. Az azonos energiájú sajátállapotok nulladrendű együtthatóihoz viszont fel kell használni λ-ban a következő rendet is. Ebben megjelenik az energiafelhasadás első rendje is, melyet így szintén megkaphatunk ebből az egyenletből. A kapott egyenlet:
Ez így rendezhető át:
Ezen homogén egyenlet megoldási feltételéből kapjuk a szekuláris egyenletet amely megadja az elsőrendű energiakorrekciókat:
Az eredeti egyenletben az elsőrendű energiakorrekciókat visszahelyettesítve megkapjuk a 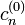 nulladrendű együtthatókat. Ezekután már használhatók a nem degenerált eset képletei.
nulladrendű együtthatókat. Ezekután már használhatók a nem degenerált eset képletei.
Időfüggő eset
Az időfüggő perturbációszámítás logikája az eddigiektől eltérő. Mivel kis hatások felhalmozódhatnak hosszú idő alatt, ezért fel szoktuk tenni, hogy a perturbáció csak rövid ideig tart. Most is hasonló sorfejtést alkalmazunk, mint az előbb a perturbálatlan feladat(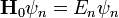 ) sajátfüggvényei szerint kifejtve a megoldást:
) sajátfüggvényei szerint kifejtve a megoldást:
Így a Schrödinger-egyenlet:
A megoldást hatványsor alakban kerssük:
A továbblépés a közönséges differenciálegyenleteknél ismert állandók variálásának módszere. (A kvantummechanikában ebből lett a kölcsönhatási kép.) Legyen:
Ez nulladrendben állandó. Ezt az álandót variálja a perturbáció jelenléte.
ahol 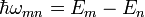 .Az első rendet megkapjuk, ha a jobb oldalon
.Az első rendet megkapjuk, ha a jobb oldalon 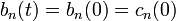 közelítést alkalmazzuk. A fenti differeniál egyenletből a b együtthatók kiszámolhatóak, segítségükkel meghatározható a végállapot hullámfüggvénye. Ismert tehát a kezdeti és a végállapot, ebből felírható a K mátrixeleme:
közelítést alkalmazzuk. A fenti differeniál egyenletből a b együtthatók kiszámolhatóak, segítségükkel meghatározható a végállapot hullámfüggvénye. Ismert tehát a kezdeti és a végállapot, ebből felírható a K mátrixeleme:
Legyen a kezdeti(i) állapot egy perturbálatlan sajátállapot: 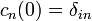 . Az átmeneti valószínűség:
. Az átmeneti valószínűség:
Fermi-féle aranyszabály
A Fermi-féle aranyszabály folytonos/kvázifolytonos spektrumban segít átmeneti valószínűségeket kiszámítani. 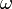 körfrekvencájú periodikus perturbáció esetén az időegységre jutó átmeneti valószínűség:
körfrekvencájú periodikus perturbáció esetén az időegységre jutó átmeneti valószínűség:
Ez a formula megkapható az előző pontból kiiindulva 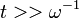 határérték elvégzésével.
Állandó perturbáció esetén:
határérték elvégzésével.
Állandó perturbáció esetén:
Ha több állapot valamelyikébe való átmeneti valószínűséget akarjuk tudni, akkor:
ahol 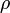 a végső állapotok sűrűsége(állapotok száma energiaegységenként)
a végső állapotok sűrűsége(állapotok száma energiaegységenként)
Elektronok kölcsönhatása sugárzási térrel, Indukált emisszió és abszorpció
Az elektromágneses tér kölcsönhat az elektronnal, az elektronra ható erő a következő:
ahol v az elektron sebessége, μ a tömege, E és H az elektromos illetve mágneses térerősség. Be lehet látni, hogy a mozgásegyenlet származtatható a
Hamiltonfüggvényből. Ez a megszokott módon operátorosítható. Ha tiszta sugárzási térbe helyezzük az elektront, akkor Φ elhagyható. Kis terekre Coulomb-mértékben vizsgálva a problémát, a következő közelítést tehetjük a perturbáló Hamilton-operátorra:
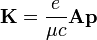 .
.
Az egyszerűség kedvéért azt a problémát vizsgáljuk, hogy egy Hidrogénatomot sugárzási térbe helyezünk, és megnézzük mit jósol a perturbációszámítás (lehetséges-e átmenet a hidrogénatom állapotai között, mekkora valószínűséggel, stb). A vektorpotenciált a következő alakúnak tételezzük fel:
Ekkor a perturbálópotenciál felírható a kvöetekző alakban:
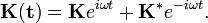 A két tag rögzített kezdőállapot esetén csak egy-egy átmenetre nem fog zérust adni. Az első tag az emissziót írja le, melynél az átmeneti valószínűség
A két tag rögzített kezdőállapot esetén csak egy-egy átmenetre nem fog zérust adni. Az első tag az emissziót írja le, melynél az átmeneti valószínűség
![W_e=\frac{2\pi}{\hbar}\left[|K_{nm}|^2\rho(E_n)\right]_{E_n=E_m-\hbar\omega}](/images/math/a/5/a/a5a88ae04b53811e6f7239426c56fbad.png) .
.
A második tag az abszorpciót írja le, melynél az átmeneti valószínűség analóg módon
![W_e=\frac{2\pi}{\hbar}\left[|K_{nm}|^2\rho(E_n)\right]_{E_n=E_m+\hbar\omega}](/images/math/b/1/9/b197a0eb30f79c03581d73d92e416aaf.png) .
.
A konkrét valószínűségekhez kiszámítandó a következő mátrixelem:
Mivel a hullámfüggvények az atomra vannak koncentrálódva, ezért 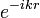 tekinthető egységnyinek, vagyis
tekinthető egységnyinek, vagyis
Ezt a sugárzást dipólsugárzásnak nevezzük (amikor elhagyjuk az exponenciálist). Ekkor ugyanis belátható, hogy a mátrixelem arányos az elektron dipólnyomatékával.
Ha a dipólnyomaték egy átmenetre zérus, akkor az átmenet nem valósul meg. Ekkor az adott átmenet tiltott. Be lehet látni, hogy az átmenet csak akkor megengedett, ha a kezdő- és végállapot között a mellékkvantumszám és a mágneses kvantumszám különbsége is pontosan 1.
Variációs módszer
Az energiasajátérték egyenlettel ekvivalens állítás az a variációs elv, amely szerint alapállapotban
az n. gerjesztett állapot pedig úgy kaphatjuk, hogy az előző szélsőértékfeladatot azon mellékfeltételekkel oldjuk meg, hogy az 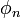 állapot ortogonális az alapállapotra és az előző n-1 gerjesztett állapotra is. Természetesen a feladat általános megoldása általában lehetetlen, ezért gyakorlati alkalmazásokban csak a Hilbert-tér egy leszűkítésén oldjuk meg, valamilyen próbafüggvényt feltételezve, majd a paraméterei szerint elvégezve a szélsőértékproblémát.
állapot ortogonális az alapállapotra és az előző n-1 gerjesztett állapotra is. Természetesen a feladat általános megoldása általában lehetetlen, ezért gyakorlati alkalmazásokban csak a Hilbert-tér egy leszűkítésén oldjuk meg, valamilyen próbafüggvényt feltételezve, majd a paraméterei szerint elvégezve a szélsőértékproblémát.
Ritz-féle variációs módszer (*)
Akkor beszélünk Ritz-féle variációs módszerről, ha a próbafüggvény valamilyen bázisfüggvények lineáris kombinációja:
Ekkor az energia várható értéke:
Ennek a c-k vagy c*-ok szerinti deriválása egy lineáris egyenletrendszerhez vezet, melynek megoldási feltétele a következő általánosított szekuláris egyenletet adja:
ahol az átfedési mátrix, mely a bázisállapotok nemortogonalitása miatt jelenik meg:
Problémák a kvantummechanika közelítő módszereivel
A perturbációszámítás gyakorlati(pl. molekulafizkai) alkalmazásakor néha problémák merülnek fel. Egyrészt előfordul, hogy az egyre újabb rendekben kapott energiák oszcillálnak, másrészt pedig előfordul, hogy úgy tűnik, mintha már bekonvergált volna a sor, de még néhány tag kiszámolása után ismét elindul. Ezek a problémák nem állnak fenn a variációs módszernél, ott legalább az irány mindig egyértelmű. De ott is előfordul, hogy az energia már nagyon közel van a jó(kísérleti) értékhez, de a hullámfüggvény még meglehetősen messze.
Azonos részecskék, Pauli-elv
A Hamilton-operátor szimmetrikus két azonos részecske(elektron) felcserélésére. Ezért a Hamilton-operátor kommutál a részecskék felcserélésével. Következésképpen választható olyan energia sajátfüggvények, amelyek a felcserélés operátorának is sajátfüggvényei. Mivel kétszeri felcserélés után az eredeti állapotba jutunk vissza, a felcserélés sajátértéke csak 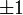 lehet, vagyis a felcseréléssel szemben a sajátállapot lehet szimmetrikus vagy antiszimmetrikus.
lehet, vagyis a felcseréléssel szemben a sajátállapot lehet szimmetrikus vagy antiszimmetrikus.
Ha áttérünk az időfüggő Schrödinger-egyenletre, akkor a permutáció operátora megmaradó mennyiség(mivel a Hamilton-operátorral felcserélhető), így a kezdeti szimmetria az időfejlődés során is megmarad.
Mint kiderült, a hullámfüggvény szimmetriája a részecske fajtájából következik:
- Feles spinű részecskék(fermionok) hullámfüggvénye antiszimmetrikus. Ebből az állításból rögtön következik, hogy az atom elektronjai közül semelyik kettő nem lehet azonos állapotban.
- Egész spinű részecskék(bozonok) hullámfüggvénye szimmetrikus.
Mivel nincsenek vegyes szimmetriájú részecskék, ezért minden részecskének tartozni kell valamelyik kategóriába. Azonos részecskék megcserélése az előzőtől megkülönböztethetetlen állapotot hoz létre. Az azonos részecskék megkülönböztethetetlenek.
Átlagtérközelítés
Nem kölcsönható azonos részecskék
Nem kölcsönható azonos részecskék esetében a Hamilton-operátor egyrészecske Hamilton-operátorok összege:
Ezesetben a Schrödinger-egyenletnek mindig léteznek szorzatalakú megoldásai:
ahol:
Ezen szorzatok viszont még nem teljesítik a Pauli-elvet. Ennek kielégítésére az egyrészecske-állapotokból Slater-determináns képezhető:
A függvények indexei jelölik, hogy melyik függvényről van szó, argumentumaik pedig azt, hogy melyik részecske koordinátái írandóak a függvénybe. Ennek látszanak a megfelelő tulajdonságai:
- Ha két részecskét(sort) felcserélünk akkor előjelet vált.
- Ha két oszlop azonos akkor nulla lesz, vagyis nem lehet két részecske azonos állapotban.
Átlagtérközelítés
Továbblépve a nemkölcsönható részekéktől a következő közelítést alkalmazhatjuk. Egy részecske helyén sok más részecskétől eredő erőt érez, ezt külső térnek tekintjük, és beírjuk az egyrészecske Schrödinger-egyenletbe. Ezt megoldva új egyrészecske sajátfüggvényeket kapunk, amelyek őj teret adnak, ezzel újraszámoljuk az egyenletet stb. Addig iterálunk, amíg a tér be nem konvergál, ezzel megkapjuk az önkonzisztens teret, vagy átlagteret.
Hartree-Fock módszer
Azt az átlagtérközelítést, amikor egyetlen Slater-determináns alakjában keressük a megoldást, és ezzel végzünk önkonzisztens-tér közelítést Hartree-Fock módszernek hívjuk. Kicsit részletesebben is megnézzük.
A variációs elvből indulunk ki. Eszerint 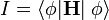 minimális. Ha a megoldást szorzatalakban keressük:
minimális. Ha a megoldást szorzatalakban keressük: 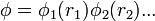 akkor az I variációjának eltünéséből az egyrészecske Schrödinger-egyenletek:
akkor az I variációjának eltünéséből az egyrészecske Schrödinger-egyenletek:
Az egylenrendszert pedig szukcesszív aproximációval oldjuk meg, első közelítésben 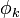 -kat hidrogénszerűnek feltételezve, és innen indítva az önkonzisztens tér közelítést. Ez a Hartree-módszer. Itt még láthatóan nem vettük figyelembe a Pauli-elvet.
-kat hidrogénszerűnek feltételezve, és innen indítva az önkonzisztens tér közelítést. Ez a Hartree-módszer. Itt még láthatóan nem vettük figyelembe a Pauli-elvet.
A Hartree-módszer továbbfejlesztése a Hartree-Fock módszer, amely Slater-determináns alakú megoldást keres:
Ekkor I variációjának eltűnése a következő egyenleteket adja:
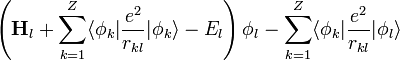 =0
=0
Ezt ugyanúgy szukcesszív approximációval oldjuk meg.
A periódusos rendszer
A kvantummechanika korai sikereinek egyike a periódusos rendszer megértése volt a Hartree-módszer alapján. Az eljárás a következő. A megoldásokat szorzat alakban keressük: 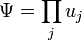 , és a Pauli-elv miatt nem engedjük meg, hogy egy
, és a Pauli-elv miatt nem engedjük meg, hogy egy 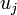 elektronpályát kettőnél több elektron töltsön be(két ellentétes spinű elektron). Az egyrészecske Schrödinger-egyenletekben szereplő átlagos potenciál mindig radiális szimmetriájúvá átlagoljuk vissza, így a kapott egyrészecske állapotok jellemezhetők az n főkvantumszámmal és l mellékkvantumszámmal. Az l főkvantumszámok hasgyományos jelölése: s,p,d,f,...
elektronpályát kettőnél több elektron töltsön be(két ellentétes spinű elektron). Az egyrészecske Schrödinger-egyenletekben szereplő átlagos potenciál mindig radiális szimmetriájúvá átlagoljuk vissza, így a kapott egyrészecske állapotok jellemezhetők az n főkvantumszámmal és l mellékkvantumszámmal. Az l főkvantumszámok hasgyományos jelölése: s,p,d,f,...
Az elektronok leárnyékolják a mag potenciáját, így ha egy elektron távolabb van a magtól, akkor kisebb potenciált érez. Az, hogy egy elektron milyen messze jár a magtól elsősorban a mellékkvantumszámától függ, hiszen ahogy pl. a hidrogénatomnál látható, a radiális hullámfüggvény 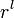 hatvánnyal indul. Másképp megfogalmazva, nagy l-re az l(l+1)-el arányos centrifugális potenciál miatt az elektron kintebb lesz. Így a magasabb l kvantumszámú állapotok gyengébben kötöttek, és megszűnik a hidrogénatomnál még meglévő l szerinti degeneráció. Azonos főkvantumszámra az l=0-tól (n-1)-ig tartó állapotok energiasajátértéke monoton nő.
hatvánnyal indul. Másképp megfogalmazva, nagy l-re az l(l+1)-el arányos centrifugális potenciál miatt az elektron kintebb lesz. Így a magasabb l kvantumszámú állapotok gyengébben kötöttek, és megszűnik a hidrogénatomnál még meglévő l szerinti degeneráció. Azonos főkvantumszámra az l=0-tól (n-1)-ig tartó állapotok energiasajátértéke monoton nő.
A Hartree-közelítés megadja az elektronpályák betöltésének sorrendjét:
1s, 2s,2p, 3s,3p, 4s,3d,4p, 5s,4d,5p, 6s,4f,5d,6p, ...
Érdemes megfigyelni, hogy a betöltött legmagasabb főkvantumszámú állapotok mindig s és p állapotok. Az atom külső határán a főkvantumszám határozza meg, hogy egy elektronpálya meddig terjed ki. Így azt találtuk, hogy a külső elektronpályák s és p pályák. Márpedig a külső pályák azok, amelyek meghatározzák a kémiai tulajdonságokat. n=1 külső héjjal 2 elem létezhet. n=2 külső héjjal 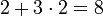 n=3-assal ismét 8 és így tovább. A kémiai tulajdonságok az s,p pályák fokozatos betöltésébel változik, hogy aztán a következő főkvantumszámmal újra kezdje. Így megértettük a periódusos rendszert.
n=3-assal ismét 8 és így tovább. A kémiai tulajdonságok az s,p pályák fokozatos betöltésébel változik, hogy aztán a következő főkvantumszámmal újra kezdje. Így megértettük a periódusos rendszert.
Viriál-tétel(*)
A kvantummechanikai viriáltétel mondja, hogy ha egy rendszer Hamilton-operátora:
ahol a potenciális energia k-adredű homogén függvény:
akkor fennáll a következő egyenlőség:
A leggyakoribb potenciálokra:
- Coulomb-potenciál k=-1
- Harmonikus oszcillátor k=2
A Born-Oppenheimer közelítés
A molekulák elméletében kiemelt jelentőségű az a tény, hogy az atommagok tömege sokkal nagyobb az elektronokénál, ezért azok sokkal lomhábban mozognak, mint az elektronok. Ez teszi lehetővé, hogy a molekula elektronproblémáját rögzített magkoordinátákkal megoldva, azokat paraméternek tekintve, majd az így kapott energiafelület minimumát megkeresve megkapjuk a molekula alapállapoti energiáját(és hullámfüggvényét). Ezt az eljárást nevezik Born-Oppenheimer közelítésnek. Az elektronprobléma megoldása több energiát ad, ezekből több potenciálfelületet kapunk. Akkor alkalmazható a közelítés, ha ezek a felületek szeparálva vannak egymástól.
Kicsit részletesebben, a Born-Oppenheimer közelítésben a hullámfüggvény:
ahol 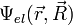 a magkoordinátáktól is függő elektronállapot,
a magkoordinátáktól is függő elektronállapot, 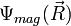 pedig a magok közelítő állapota. A Hamilton-operátor:
pedig a magok közelítő állapota. A Hamilton-operátor:
ahol az elektron Hamiltonja a kinetikus energiájuk, a magok vonzása és az elektronok egymás közti taszításának összege:
és a magok Hamiltonja a kinetikus energiájuk és egymás közti taszításuk összege:
A lassan változó magkoordinátáktól függő elektron sajátérték probléma:
Adiabatius közelítésben az a közelítő potenciál, amelynek minimuma a kémiailag kötött állapotot jelenti:
Ezen minimum körül alakulnak ki a molekularezgések, amelyek kis gerjesztésnél harmonikusak, nagyobb gerjesztésnél anharmonikusak. Még nagyobb gerjesztés disszociációhoz, kémiai reakcióhoz vezet.
Formálisan úgy kapható meg a közelítés, mint az 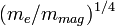 kis paraméter szerinti sorfejtés vezető tagja. Akkor romlik el a közelítés, ha az elektronok is lassan mozognak. Ahol egy
kis paraméter szerinti sorfejtés vezető tagja. Akkor romlik el a közelítés, ha az elektronok is lassan mozognak. Ahol egy 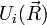 és
és 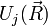 szint keresztezi egymást, ott van lassú mozgás, ott keverednek a molekula különböző gerjesztései. Az ilyen kevert gerjesztési módust polaritonnak hívják.
szint keresztezi egymást, ott van lassú mozgás, ott keverednek a molekula különböző gerjesztései. Az ilyen kevert gerjesztési módust polaritonnak hívják.
Hellmann-Feynman tétel (*)
A Hellmann-Feynman tétel szerint:
ahol E a 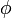 hullámfüggvényhez tartozó energia,
hullámfüggvényhez tartozó energia, 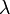 pedig valamilyen paraméter. Ezen tétel segítségével ki tudjuk számolni a molekulában a magokra ható erőket, amiből lehet egyensúlyi magtávolságokat számolni, ekkor
pedig valamilyen paraméter. Ezen tétel segítségével ki tudjuk számolni a molekulában a magokra ható erőket, amiből lehet egyensúlyi magtávolságokat számolni, ekkor 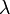 helyére a magkoordinátákat kell írni és ekkor tulajdonképpen a potenciál helyszerinti deriváltja áll a képletben, ami mint tudjuk az erő (-1 szerese).
helyére a magkoordinátákat kell írni és ekkor tulajdonképpen a potenciál helyszerinti deriváltja áll a képletben, ami mint tudjuk az erő (-1 szerese).
A kémiai kötés
A kvantummechanika egyik nagy sikere volt a kovalens kötés megmagyarázása. A kötés azért jöhet létre, mert a kötött rendszer energiája alacsonyabb, mint az atomok energiájának összege. Ez azért van, mert az elektronok hullámfüggvénye besűrűsödik az atomok köze. Ekkor:
- Coulomb-potenciálban a viriál-tétel miatt:
Ha a magok között az elektronok összesűrűsödnek, akkor a magok vonzó potenciálja összeadódik, ami mélyebb eredőt eredményez.
- Egy helyről lehet két magot egymás felé vonzani.(Hellmann-Feynmann tétel)
Vannak olyan effektusok is, amelyek a sűrűsödést akadályozzák:
- Kisebb helyre szorulás a kinetikus energia növekedésével jár.
- Az elektronok közötti Coulomb-taszítás
- Pauli-elv akadályozza sok azonos spinű elektron összegyülekezését kis helyre, emiatt egy-egy molekulapályán ellentétes spinű elektronokból párok alakulhatnak ki
Ez kvalitatív kép. A kvantitatív számolások nehezek.
A hidrogén atom
A Schrödinger-egyenlet megoldása Coulomb-potenciálban
Ennek megjegyzése szerintem annnyira nem fontos.
A szögfüggő tagok leválasztása után:
Bevezetve 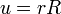 -t:
-t:
Ezek után dimenziótlanítunk. Legyen 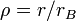 és
és 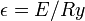 , ahol a Bohr-sugár
, ahol a Bohr-sugár 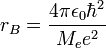 és a Rydberg-állandó
és a Rydberg-állandó 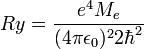 . Ekkor:
. Ekkor:
A szükséges határfeltételek:
-
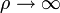 -ben u=0.
-ben u=0.
-
 -ban?
-ban?
Ha 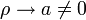 akkor
akkor 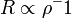 , erre hattatva a Laplace operátort az origóban Dirac-deltát kapunk, vagyis nem elégítjük ki a Schrödinger-egyenletet. Ezért itt is u=0 lesz a határfeltétel.
, erre hattatva a Laplace operátort az origóban Dirac-deltát kapunk, vagyis nem elégítjük ki a Schrödinger-egyenletet. Ezért itt is u=0 lesz a határfeltétel.
Az egyenlet megoldási módszere Sommerfeld féle polinom módszer:
- Megoldjuk az egyenletet aszimptotikusan.
Az aszimptotikus megoldás 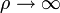 -ben
-ben 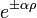 ahol
ahol 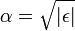 . A norma miatt csak a negatív előjel jó.
. A norma miatt csak a negatív előjel jó.
- A megoldást
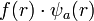 alakban keressük, ahol
alakban keressük, ahol 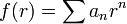 hatványsor. Az f(r) eredeti egyenletbe való visszahelyettesítése után kapunk egy rekurziót az
hatványsor. Az f(r) eredeti egyenletbe való visszahelyettesítése után kapunk egy rekurziót az 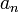 -ekre.
-ekre. - A rekurzió megoldása elrontja az aszimptotikát, az egyetlen megoldás, ha a hatványsorunk véges, vagyis valamilyen n-re
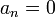 . Ebből a feltételből közvetlenül kapjuk az energiaszinteket. Az együtthatók kiszámolásával pedig a sajátfüggvényeket.
. Ebből a feltételből közvetlenül kapjuk az energiaszinteket. Az együtthatók kiszámolásával pedig a sajátfüggvényeket.
Az energiaszintek:
Minden energiaszint 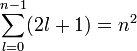 -szeresen degenerált.
-szeresen degenerált.
Atomi energianívók termjelölése
Az atomi energianívókat jellemző kvantumszámok:
n - főkvantumszám (1,2,3,4,... vagy K,L,M,N,...)
l - mellékkvantumszám, az eredő pályaimpulzusmomentum kvantumszáma (0,1,2,3... vagy S,P,D,F,...)
s - eredő spinkvantumszám
j - teljes impulzusmomentum, értéke |l-s|-től l+s-ig változhat
m_j - mágneses kvantumszám: j,j-1,...,-j
A hagyományos jelölés:
Pl.: a nátrium alapállapota 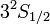
Mágneses momentumok
Az elektron pályimpulzusához tartozó mágneses momentum:
Az elektronspinhez tartozó mágneses momentum:
A magspinhez tartozó mágneses momentum:
Itt L az elektron pályamomentuma, S a spinje, I a magspin. A Bohr-magneton:
A magmagneton:
A különböző g-faktorok értéke elektronpályára 1, elektronspinre 2(pontosabban 2,00232). Ez első adódik a klasszikus kvantummechanikából, a második a Dirac-egyenletből. A különböző atommagok g-faktorai, vagy giromágneses faktorai táblázatban megtalálhatóak. A mag-giromágneses faktor:
Finomfelhasadás
A spektrumvonalak első korrekciója a relativisztikus hatások figyelembevétele miatt keletkezik. Ez a hidrogén esetében az egyébként csak a főkvantumszámtól függő energiaszintek szeparációját hozza magával. Az effektus nagyságrendje: 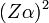 , ahol Z a rendszám,
, ahol Z a rendszám, 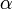 a finomszerkezeti-állandó, így a nagyságrend kb.
a finomszerkezeti-állandó, így a nagyságrend kb. 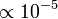 . Ez az effektus több hatás összegése, tartalmazza a spin-pálya kölcsönhatást, a relativisztikus energiakorrekciót és egy kiátlagolt elektronmozgási potenciált.
. Ez az effektus több hatás összegése, tartalmazza a spin-pálya kölcsönhatást, a relativisztikus energiakorrekciót és egy kiátlagolt elektronmozgási potenciált.
Spin-pálya kölcsönhatás
A finomfelhasadást részben okozó spin-pálya kölcsönhatás úgy tekinthető, mint a spin mágneses momentumának energiája az atom belső mágneses terébe, mely az elektronok mozgásából ered. A belső tér a pályaimpulzus-momentummal, a spin mágneses momentuma a spinnel arányos, ezért:
Mivel:
és S=1/2, ezért két energiaszint lesz, az j=l+1/2 energiája nagyobb mint a j=l-1/2 szinté. A felhasadás nem szimmetrikus.
Hiperfinom felhasadás
A spektrumvonalak az elektronok maggal való mágneses kölcsönhatásának és az atommag helyén levő elektromos tér hatására kialakuló magelektromos kvadrupól momentum hatásának következtében további felhasadásoknak lesznek kitéve. Általánosságban ezek a finomszerkezetnél még legalább egy nagyságrenddel kisebb effektusok.
A magmágneses dipólmomentum hatása
A magmágneses dipólmomentum kölcsönhatása a valenciaelektronok által a mag helyén keltett mágneses térrel egy nagyon kis mértékű felhasadást okoz az atomi spektrumokban. Hasonlóan a spin-pálya kölcsönhatáshoz, a hozzá tartozó Hamilton felírható ilyen alakban:
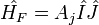
Ahol a teljes impulzumomentum F=I+J. A felhasadás innen:
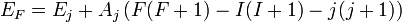
Lamb shift
A Dirac-egyenlet szerint az azonos j-khez és különböző l-ekhez tartozó nívók a hidrogén spektrumában elfajultak. Lamb és Retherford(1947) kísérletileg kimutatta, hogy a hidrogén 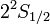 és
és 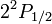 nívói 1058MHz frekvenciával elkülönülnek. A felhasadás máshol is jelen van, de jóval kisebb. A Lamb-shift az elektromágneses tér zérusponti energiájának fluktuációjával kapcsolatos, kvantumelektrodinamikával pontosan számolható.
nívói 1058MHz frekvenciával elkülönülnek. A felhasadás máshol is jelen van, de jóval kisebb. A Lamb-shift az elektromágneses tér zérusponti energiájának fluktuációjával kapcsolatos, kvantumelektrodinamikával pontosan számolható.
A hélium atom
A legegyszerűbb elméleti módszer a héliumatom kezelésére a következő. A Hamilton-operátorban a két elektron taszítását H' perturbációnak tekintjük, így a Hamilton-operátor két H-atom Hamilton-operátor és egy perturbáció összege:
a két H-atom operátor összegének sajátértékproblémája:
ahol a 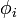 -k H-atom sajátállapotok. Ezekután a degenerált perturbációszámítás képleteit használva a szekuláris egyenlet:
-k H-atom sajátállapotok. Ezekután a degenerált perturbációszámítás képleteit használva a szekuláris egyenlet:
Ami alajpán az energiaszintek:
Coulomb-integrál:
Kicserélődési integrál:
Ilyen alakú integrálok folyton előjönnek atom- és molekulafizikai számításoknál. A nulladrendű közelítés hullámfüggvényeire pedig rendre:
adódik. A spint és a Pauli-elvet figyelembe véve a következőt mondhatjuk. A szimmetrikus térbeli hullámfüggvény antiszimmetrikus spinhullámfüggvénnyel(szinglet) szorzódik:
Az antiszimmetrikus térbeli hullámfüggvény szimmetrikus spinhullámfüggvények valamelyikével(triplet) szorzódik szorzódik:
Alapállapotban csak a szinglet valósul meg, hiszen k=l miatt a másik esetben a helyfüggő hullámfüggvény azonosan nulla.
Stark-effektus
Az atom energiájának elektromos tér által bekövetkezett falhasadását Stark-effektusnak nevezzük. Az első gerjesztett állapot Stark-effektusa a perturbáció számítás első közelítésében arányos az elektromos térerősséggel, ezért lineáris Stark-effektusnak nevezzük. A lineáris Stark-effektus szimmetrikus felhasadást eredményez. A négyszeres degeneráció kétszeresre csökken. A H-atom esetében:
A lineáris Stark-effektus csak hidrogénszerű állapotokra lép fel, vagyis akkor, ha az energia csak az n főkvantumszámtól függ, és az állapotok l szerint elfajultak. Az energia meváltozása a perturbációszámítás második rendjében jelenik meg:
ahol 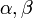 állandók, m a mágneses kvantumszám.
állandók, m a mágneses kvantumszám.
Zeeman-effektus
A Zeeman-effektus az aránylag kis mágneses tér hatására bekövetkező, egyébként degenerált energiaszintek felhasadása. A mágneses térnek olyan értelemben kell kicsinek lennie, hogy az az alapállapot Hamilton-hoz perturbációként járuljon hozzá:
Ahol a perturbáció az atomi mágneses momentum és a mágneses tér szorzata:
Az atomi mágneses momentumhoz a mag is hozzájárul, azonban ez több nagyságrendel kisebb az elektron járulékánál, így elhanyagolható. A mágnesesmomentum a teljes impulzusmomentumot tartalmazza. Ha a spin-pálya csatolás erős, akkor csak a teljes impulzusmomentum marad állandó, szemléletesen a pálya- és spin momentumok precesszálnak az állandó teljes impulzusmomentum körül. Kiátlagolva időben a két nemmegmaradó momentumot:
Ezeket beírhatjuk a mágnesesmomentum kifejezésébe, megszorozva a megfelelő giromágneses faktorokkal, és így megkapjuk az időátlagolt perturbációt. Behelyettesítve, és a z-vetületet véve a perturbáció:
Ahol 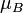 a Bohr-magnetron, és g_j a felhasadást a kvantumszámok függvényében megadó Landé-faktor:
a Bohr-magnetron, és g_j a felhasadást a kvantumszámok függvényében megadó Landé-faktor:
A 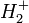 molekulaion, kicserélődési kölcsönhatás(*)
molekulaion, kicserélődési kölcsönhatás(*)
Kétatomos molekulák
Általános megjegyzések
- A tér szimmetrikus a két atommagon átmenő tengelyre, ezért az impulzusmomentum ezen tengelyre vett vetülete megmarad. Ezt a vetületet
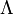 -val szokás jelölni, és 0,1,2 értékei esetén rendre
-val szokás jelölni, és 0,1,2 értékei esetén rendre 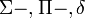 -termről beszélünk.
-termről beszélünk. - A molekula tengelyét tartalmazó síkre való tükrözés az impulzusmomentum előjelét megfordítja(axiálvektor). Következik, hogy a
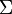 -termek kivételével a többi kétszeresen elfajult(ezek a sajátfüggvények az impulzusmomentum előjelében különböznek). Egy
-termek kivételével a többi kétszeresen elfajult(ezek a sajátfüggvények az impulzusmomentum előjelében különböznek). Egy 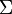 -term tükrözés esetén egy állandóval szorzódhat, mivel kétszeres tükrözés azidentitással egyenlő ez az állandó
-term tükrözés esetén egy állandóval szorzódhat, mivel kétszeres tükrözés azidentitással egyenlő ez az állandó 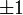 , ezek alapján szokás
, ezek alapján szokás 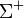 és
és 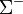 termekről beszélni.
termekről beszélni.
- Két azonos atomból álló molekula szimmetrikus az atommagokat összekötő szakasz felezőpontjára is. Az erre való tügrözés szerint beszélhetünk páros(h) és páratlan(u) állapotokról. Ez utóbbi az elektronkoordináták előjelének megváltoztatásakor előjelet vált. Jelölés pl.:
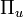
- Empirikus szabály: kémiailag stabil kétatomos molekulák túlnyomó többségének alapállapota teljesen szimmetrikus(a molekula minden szimmetriájára invariáns)
- Termeket ábrázolhatjuik grafikusan a magtávolság függvényében. Tétel: Csak különböző szimmetriájú termek metszhetik egymást.
A vegyérték
Tekintsük a 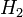 molekulát. Ennek a legalacsonyabb impulzusmomentumú lehetséges termjei az
molekulát. Ennek a legalacsonyabb impulzusmomentumú lehetséges termjei az 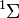 spinszinglett állapot és a
spinszinglett állapot és a 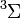 spintriplett állapot. A spintriplett szimmetrikus spinhullámfüggvényt jelent, ami a Pauli-elv miatt antiszimmetrikus helyhullámfüggvényt. Azonban egy antiszimmetrikus helyhullámfüggvény
spintriplett állapot. A spintriplett szimmetrikus spinhullámfüggvényt jelent, ami a Pauli-elv miatt antiszimmetrikus helyhullámfüggvényt. Azonban egy antiszimmetrikus helyhullámfüggvény 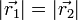 -nél eltűnik, így nem lehet az alapállapot. Kémiában szokásos kifejezés szerint csomósíkja van az elektronpályának. Részletes számolás szerint valóban a
-nél eltűnik, így nem lehet az alapállapot. Kémiában szokásos kifejezés szerint csomósíkja van az elektronpályának. Részletes számolás szerint valóban a 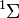 termnek a magtávolságfüggvényében minimuma van, míg a
termnek a magtávolságfüggvényében minimuma van, míg a 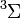 termnek nincs(lazító állapot), így az alapállapot a
termnek nincs(lazító állapot), így az alapállapot a 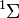 term. Vagyis alapállapotban a spin 0. Mind kiderül, a főcsoport elemeinek majdnem minden kémiailag stabil molekulája rendelkezik ezzel a tulajdonsággal. Azt, hogy az ilyen típusú, tisztán kvantummechanikai kötés(kovalens kötés, azaz mindkét atomra kiterjedő molekulapályák által alkotott kötés) a spinnel kapcsolatos, Heitler és London felfedezése volt. Ez teszi lehetővé a vegyérték fogalmának bevezetését. Egy atom vegyértéke egy atom spinjének kétszerese, ami a körülötte található elektronok spinjének összege. Atomok egyesülése során pedig a vegyértékeknek kölcsönösen telítődnie kell, vagyis egy atom minden vegyértékkötésének meg kell feleljen egy másik atom vegyértékkötése.
term. Vagyis alapállapotban a spin 0. Mind kiderül, a főcsoport elemeinek majdnem minden kémiailag stabil molekulája rendelkezik ezzel a tulajdonsággal. Azt, hogy az ilyen típusú, tisztán kvantummechanikai kötés(kovalens kötés, azaz mindkét atomra kiterjedő molekulapályák által alkotott kötés) a spinnel kapcsolatos, Heitler és London felfedezése volt. Ez teszi lehetővé a vegyérték fogalmának bevezetését. Egy atom vegyértéke egy atom spinjének kétszerese, ami a körülötte található elektronok spinjének összege. Atomok egyesülése során pedig a vegyértékeknek kölcsönösen telítődnie kell, vagyis egy atom minden vegyértékkötésének meg kell feleljen egy másik atom vegyértékkötése.
A 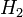 molekula(*)
molekula(*)
Molekulák rezgési és forgási spektruma
Az eddigi leírások az áló molekulákra vonatkoztak. Egy molekula azonban végezhet forgó mozgást is, amely szintén kvantált, azaz csak diszkrét energiákat vehet fel, és csak diszkrét kvantumokban gerjeszthető. Ezenfelül a molekulákban, ha megfelelő a potenciálfelület és az molekula geometriájához képesti alapállapotbeli eltérések harmonikus oszcillátorként közelíthetőek, akkor ezek a kötések is gerjeszthetőek a rezgés módusának megfelelő energiájú fotonokkal. Tipikusan a rezgési gerjesztési hullámhossz a közép-infravörös (30–2.5 μm) tartományába esik, az ennél kisebb energiájú forgási gerejsztések kisebb energián, a távoli-infravörösben (1000–30 μm) vannak. Mivel ezek a kisenergiájú gerjesztések igen érzékenyek és specifikusak a molekula geometriájára, illetve az elektronok potenciálfelületeire, ezért egyedülállóan pontos szerkezet- és anyagmeghatározási lehetőségeket biztosítanak. Ez vezetett a megfelelő spektroszkópiák kialakulásához.
Kis gerjesztések esetén a rezgési spektrum közelíthető harmonikus oszcillátorként, kétatomos molekulákra:
ahol
ahol 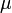 a molekulatömeg, k a kémiai kötés erősségére jellemző erőállandó. Többatomos molekulákra a rezgési spektrum első körben több független oszcillátorral közelíthető:
a molekulatömeg, k a kémiai kötés erősségére jellemző erőállandó. Többatomos molekulákra a rezgési spektrum első körben több független oszcillátorral közelíthető:
A forgási energia pedig első körben merev rotátorként képzelhető el. Mivel a forgási energia lényegesen kisebb a rezgésinél, ezért első körben a kettő tekinthető függetlennek.
IR- és Raman-spektroszkópia
Az IR (infravörös) spektroszkópia összefoglaló neve a forgási és rezgési spektrumok tanulmányozására szolgáló spektroszkópiai módszereknek. Az egyes rezgések igen határozottan specifikusak az egyes molekuláris csoportokra, illetve kötésekre, sőt a spektrumvonalak finomszerkezete az izotópokra is érzékeny. Az elméleti számolások itt igen elbonyolodnakm sokszor nem élhetünk az energiaszintek adiabatikus közelítéssel sem. A forgásispektroszkópiának további hátránya, hogy csak gázfázisban használható, mert folyadékban és gázokban az ütközések elnyomják a hatását. Továbbá szükséges hozzá (első közelítésben), hogy legyen a molekulának eredő dipólmomentuma.
Az fenti módusok gerjesztésének egyik más módszere a Raman-spektroszkópia, ez a fotonok rugalmatlan szórása a különböző gerjeszthető részeken (fononokon, molekuláris elektronfelhőn, kémiai kötéseken), aminek következtében energiát ad át az adott módusnak, ami által megváltozik a besugárzott foton frekvenciája és az észlelt spektrumban vonalak jelentkeznek. Ezzel párhuzamosan a felgerjesztett módus egy idő után visszatér az alapálapothoz közeli, de gerjesztett szintre. Az alapvető különbség az infravörös és a Raman-spektroszkópia között, hogy az infravörösnél beusgárzott foton elnyelődik, és közvetlenül csak a rezgést gerjeszti, míg a Raman spektroszkópiánál egy jóval magasabb szintre történő gerjesztés utáni visszaállás vezet ugyanarra az energiaszintre.
Ha az alapállapotból történő gerjesztés után a visszatérés az alapállapotba történik, az a klasszikus Rayleigh folyamat. Ha a visszatérés magasabb szintre történik, például az előbb részletezett esetben, akkor Stokes-folyamatról, ha kicsit gerjesztett állapotból mélyebb állapotba térünk vissza, akkor anti-Stokes folyamatról beszélünk.
Alagút-effektus
Tekintsünk egy rendszert, ahol a hullámfüggvénynek az egyik közegben exponenciálisan lecsengő megoldása van, de a közeg két végén oszcilláló megoldása. Ha a közeg egyik oldalán például felveszünk egy hullámcsomagot, ami adott sebességgel halad az exponenciálisan lecsengő régió felé, akkor véges valószínűsége lesz annak, hogy a hullámcsomag átjut a közegen, és a másik oldalon folytatja útját. Ilyen jelenség van például az atommagban az alfarészecskékkel.
Hivatkozások:
- ↑ Az első négy alrészről lásd Geszti Tamás: Kvantummechanika, Typotex, Bp., 2007, 13. fej.: Perturbációszámítás (165-190)