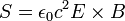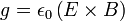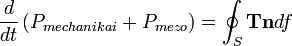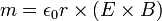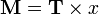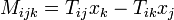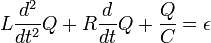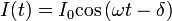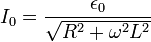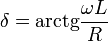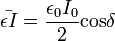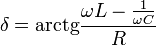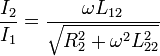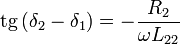Elektrodinamika
Tartalomjegyzék
A Maxwell-egyenletek
A teljes Maxwell-egyenletek differenciális alakban a következőek:
Az első egyenlet az áram mágneses hatását fejezi ki: azaz mágneses hatást a változó elektromos tér, illetve a folyó áram kelt. Az második egyenlet azt fejezi ki, hogy az elektromos tér forrásai a töltések. A harmadik egyenlet szerint a változó mágneses tér elektromos teret kelt. A negyedik egyenlet szerint a mágneses térnek nincs töltése (nincs mágneses monopólus). Az egyenletek kissé variálhatóak kihasználva, hogy:
Ezek az egyenletek térrészenként érvényesek. Megfogalmazhatóak a fenti egyenletek integrális alakban is, azok a határokon is leírják a térmennyiségeket, míg a differenciálisokhoz ezeket külön hozzá kell kapcsolni. Továbbá a Maxwell-egyenletek nem tartalmazzák az anyagi hatásokat, azokat külön egyenletekkel kell csatolni, amelyek E és D továbbá B és H közötti kapcsolatokat írják le. Ezen felül a Lorentz-erő sem vezethető le klasszikusan a fentiekből:
Az egyenletek implicite tartalmazzák a töltésekre vonatkozó kontinuitási egyenletet, amit például az első egyenlet divergenciájából vezethetünk le:
Indukció
Stacionárius áram közelítés: feltesszük, hogy nincs jelen változó elektormos tér, így az ennek megfelelő tag hiányzik a harmadik Maxwell-egyenletből.
Nyugalmiindukció
Az időben változó mágneses tér elektormos teret kelt. A harmadik Maxwell-törvény integrális alakját használva:
Ahol U az indukált feszültség, 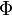 a mágneses fluxus.
a mágneses fluxus.
Mozgásiindukció
A mágneses térben mozgó vezetőben áram indukálódik a Lorentz-erő miatt.
Ha veszünk egy mágneses térben levő téglalap alakú áramkört, amelynek egyik éle L hosszúságú, és ezt a részét mozgatjuk v sebességgel, így a másik él hossza x(t) szerint változik. Ekkor ez áramot tud hajtani az áramkörben:
Itt felismerhetjük az áramkör keresztmetszetét, így voltaképpen ismét a fluxusváltozás jelenik meg:
Kölcsönös- és önindukció
Vegyünk egy áramkörnek egy hurkát (k-dikat) hurkot, és integráljuk körbe az elektromos térerősséget. Kirchhoff huroktörvénye miatt az összes feszültség nulla lenne, ha nem lenne változó mágneses tér. Azonban ha ez mégis jelen van, akkor az megjelenik a jobboldalon:
A baloldalra beírjuk az Ohm-törvényt, és az elektromotoros erőt, a jobboldalra a vektorpotenciált:
Mivel a teljes körre integrálunk, az Ohm-törvényt beírhatjuk a klasszikus formában az áramerősséggel kifejezve, az elektromotoros erőt pedig az összes potenciáljával helyettesítjük. A jobboldalon alkalmazzuk a Stokes-tételt, így a felületi integrált vonalintegrálra írjuk át:
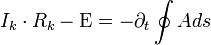
A jobboldalra beírhatjuk a lineáris vezető vektorpotenciáljának képletét:
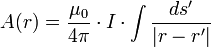
Visszaírva:
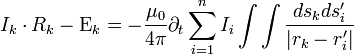
Az integrálokra a konstansokkla egybeolvasztva bevezetjük az indukciós együtthatót, L-et:
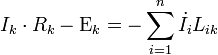
Amennyiben L-nek a két indexe azonos, akkor az áramkörben folyó áram által keltett mágnesestérnek az áramkörre való visszahatásának együtthatójáról, azaz az önindukciós együtthatóról beszélünk. Ellenkező esetben kölcsönös indukcióról van szó, azaz egy másik áramkörrészben folyó változó áram kelt ebben az áramkörben feszültséget a mágneses hatása révén.
Az elektromágneses tér makroszkópikus mennyiségei
Energia
Tekintsük első és a harmadik Maxwell-egyenlet. Az elsőt szorozzuk meg 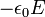 -vel, a harmadikat
-vel, a harmadikat 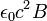 -vel, adjuk össze, és integráljuk ki térfogatra:
-vel, adjuk össze, és integráljuk ki térfogatra:
Itt kihasználtuk a jobboldalon, hogy 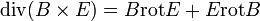 . A baloldali integrandus az energiasűrűség (jel.: u). A jobboldali első tag tartalmazza a konvektív töltéseken végzett munkát, a Joule-hőt, a telep által szolgáltatott energiát. A második tag a tekintett térfogat felületén átáramlott elektromágneses energiát jelenti, például hullámok formájában. Ez alapján definiáljuk a Poynting-vektort, másnéven energiasűrűség-vektort:
. A baloldali integrandus az energiasűrűség (jel.: u). A jobboldali első tag tartalmazza a konvektív töltéseken végzett munkát, a Joule-hőt, a telep által szolgáltatott energiát. A második tag a tekintett térfogat felületén átáramlott elektromágneses energiát jelenti, például hullámok formájában. Ez alapján definiáljuk a Poynting-vektort, másnéven energiasűrűség-vektort:
Impulzus
Definiálhatjuk az impulzussűrűséget is:
Ha az impulzus megmaradást is fel akarjuk írni:
Itt S egy felület, amely egy V térfogatot határol, n a felület kifelé mutató normálvektora, a jobboldalon felületi integrál van az S felületre, az integrandusban a Maxwell-féle feszültségtenzor jelent meg (részletesebben lásd itt). A Tn szorzat az S felület egységnyi részén egységnyi idő alatt a V térfogatba áramló impulzus. Az így definiált impulzus segítségével értelmezhető egyszerűen például Lebegyev fénynyomásos kísérlete.
Impulzusmomentum
Definiálhatjuk az elektromágneses mező impulzusmomentum-sűrűségét is:
Az impulzusmomentum fluxusa megint a Maxwell-feszültésgtenzorral fejezhető ki:
Vigyázat: M már harmadrendű tenzor! Komponensenként kiírva:
RLC elemek, áramkörök
RLC körnek nevezzük az olyan áramkört, amelyben ellenállás, induktivitás, és kapacitás is található. Az induktivitásban az áramerősség nem változhat ugrásszerűen, a kondenzátoron a feszültség. Általánosan a következő differenciál egyenletet írhatjuk fel:
A jobboldalon az áramforrások elektromotoros erejei állnak összevonva. Ez a differenciál-egyenlet teljesen analóg a mechanikai kényszerrezgésekkel, ezért a megoldása is hasonló eredményekre vezet, exponenciális lecsengésre, vagy periodikus, de csillapított rezgésre.
Az áramkörökre fontosak továbbá a Kirchhoff-törvények, amelyek nem önállóak, levezethetőek a Maxwell-egyenletekből.
- Huroktörvény: Egy zárt áramköri hurokban a feszültségek előjeles összege zérus (feltéve, hogy nincs külső mágneses tér).
- Csomópont-törvény: Az egy áramköri csomópontban összefutó áramok előjeles összege zérus.
Rezgőkör
Tekintsünk egy RL-kört, amelyet egy periodikus feszültségforrás táplál. Mivel most nincs kapacitás, az előző pontban felírt differenciálegyenletből elhagyható a kapacitásos tag, és átírható az egyenlet áramerősségre, így csupán egy elsőrendű egyenletet kell megoldanunk. A megoldásra egy tranziens lecsengő, és egy stacionárius tagot kapunk. Mivel az áramkörökben gyakorlati szempontból igen gyorsan beáll az egyensúly, elég ha a stacionáriust vizsgáljuk. Ebből látható, hogy a megoldás áramerősség frekvenciája ugyanakkora, mint a feszültségforrásé, azonban ahhoz képest késik:
Érdemes megjegyezni, hogy a Joule-hő összefügg a rezgőkör paramétereivel:
Általános RLC körben azt érdemes tudni, hogy az áramkörbe tett kapacitás hatására az áramerősség sietni, induktivitás hatására késni fog az elektromotoros erőhöz képest. Az általános formula:
Transzformátor
A transzformátor feltalálását Nikola Tesla nevéhez kötik. A transzformátorban két induktíven csatolt tekercs van, azaz a bármelyik tekercs mágneses fluxusa átmegy mindkét tekercsen. Az eredmény az, hogy ha váltakozó feszültséggel tápláljuk meg az egyik tekercset, akkor az változó mágnesesteret kelt, az pedig a másik tekercsben változó áramot indukál. A váltakozás frekvenciája ugyanaz mindkét áramkörben! Egyedül az áramerősségek értékeiben lesz különbség. A szekunder és primer körök közötti amplitúdó aránya:
Ahol 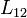 a két áramkör kölcsönös indukciós együtthatója,
a két áramkör kölcsönös indukciós együtthatója, 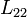 a szekunder tekercs önindukciós együtthatója,
a szekunder tekercs önindukciós együtthatója, 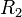 a szekunder oldal ohmikus ellenállása, azaz a nevezőben a második kör impedanciája szerepel. Tehát az átfolyó áramot a kölcsönös indukció erőssége és a kör impedanciájának mértéke szabja meg. Fellép egy fáziskésés is a két tekercs között, ennek mértéke:
a szekunder oldal ohmikus ellenállása, azaz a nevezőben a második kör impedanciája szerepel. Tehát az átfolyó áramot a kölcsönös indukció erőssége és a kör impedanciájának mértéke szabja meg. Fellép egy fáziskésés is a két tekercs között, ennek mértéke:
Váltakozóáram
Mivel a Joule-hő veszteség az áramnak négyzetes függvénye, ezért az elektromos áram szállítását célszerű minél kisebb áramerősséggel tenni, ez az állandó ellenállás mellett nagy feszültséget jelent. Azonban a felhasználás során általában kisfeszültségre és nagy áramra van szükség. Ezért az elektromos távvezetékek két végén transzformátorok vannak, amelyek a feszültséget (áramot) konvertálják. Az egész rendszer tradicionálisan a XIX. század végén alakult ki. Az egész eljárás csak aránylag nagy távolságokon éri meg, kis távolságokra, és speciális helyeken (például tengeri kábelekben) nagyfeszültségű egyenáramot használnak szállításra.
Elektromos áram a mindennapokban
Előállítás
Az elektromos áramot a kisszámú félvezető elven működő naperőműtől eltekintve valamilyen forgómozgásból nyerik, ahol ezt a mozogást periodikusan változó mágnesestérrel elektromos áram indukálására használják fel. A kezdeti forgómozgást például a széllel meghajtott lapátkerék, vízzel meghajtott turbina, vagy gőzzel meghajtott turbina szolgáltathatja. Az első két esetben a mozgó közeg természetesen rendelkezésre áll. A gőzzel hajtott esetben a gőz előállításához valamilyen hőforrás szükséges, ez vagy valamilyen éghető anyag felhasználásával (tőzeg, lignit, kőszén, olaj, gáz), vagy atomenergiával történik. A felsorolt tüzelőanyagok korlátossága miatt egyre nagyobb figyelem fordítódik ezek kiváltására megújuló vagy alternatív (fúziós erőmű) energiatermelési eljárások alkalmazásával.
Szállítás
Lásd feljebb.
Felhasználás
Igen sokrétű, mivel mind mágneses, kémiai, biológiai hatása van, ezenfelül könnyen és egyszerűen szabályozható, és sok nagyságrenden keresztül megbízhatóan alkalmazható.
Motorok
A motorok az áram mágneses hatását alkalmazzák forítva, mint a generátorok, itt a bejövő áram hatására a mágneses forgórész kerül mozgásba. Megkülönböztetünk egyenáramú és váltóáramú motorokat, valamint léptető motorokat. Különböző alkalmzásokra és különböző árra különböző típusú motorokat alkalmaznak. lásd: itt.
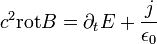
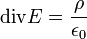
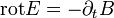
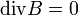
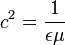
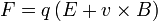
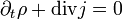
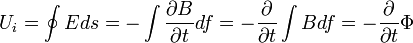
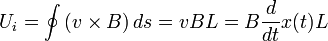
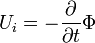
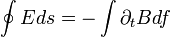
![-\frac{d}{dt} \int \left[ \frac{\epsilon_0}{2} E^{2} + \frac{\epsilon_0c^{2}}{2}B^{2}\right] dV = \int Ej dV - \epsilon_0c^{2} \int \operatorname{div}( B \times E ) dV](/images/math/b/3/6/b362e807c80aa0bfa1d688a371815a17.png)