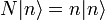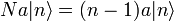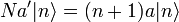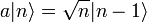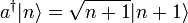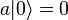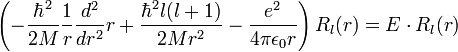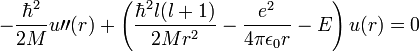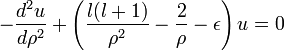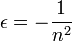Egzaktul megoldható fizika problémák
Tartalomjegyzék
Rezgések
Harmonikus oszcillátor
Az egész kvantitatív fizika legalapvetőbb megoldható rendszere a harmonikus oszcillátor. Ez egy olyan tömegpont mozgása, amely 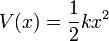 alakú potenciálban végez csillapítatlan rezgőmozgást. Ekkor:
alakú potenciálban végez csillapítatlan rezgőmozgást. Ekkor:
És a mozgásegyenlet:
Az általános matematikai alak:
Ennek megoldása:
A kezdőfeltételek határozzák meg A-t és 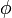 -t, a körfrekvenciára:
-t, a körfrekvenciára:
Csillapított és gerjesztett harmonikus oszcillátor
A fenti probléma két további, bonyolított változata is egzaktul megoldható. Hozzáadhatunk az egyenlethez, egy sebességgel arányos csillapítást:
Ekkor a megoldás:
Három elkülönülő régió van, a négyzetgyök alatti mennyiség előjele alapján:
- Ha negatív: alulcsillapított, létrejön oszcilláció, ami lecseng,
- Ha nulla: kritikusan csillapított, egy félhullám lehet az egyensúly felé tartásban, de nincs nullátmenet,
- Ha pozitív: túlcsillapított: a kitérés mindig az egyensúlyi helyzet felé húz, hullámok nélkül.
A fenti differenciál-egynlethez állandó periodikus gerjesztőerőt is hozzáadhatunk:
Az előbb részletezett három régió most is ugyanaz, a kezdeti állapotból a rendszer a csak csillapítottnál megfigyelhető relaxációval kerül be a gerjesztési amplitúdó és frekvencia által megszabott oszcillációhoz. Az explicit megoldásokat lásd itt.
Regések összetétele
Egyszerű trigonometriával belátható, hogy azonos frekvenciájú, de tetszőleges amplitudójú és fázisú harmonikus rezgőmozgások eredője is harmonikus rezgőmozgás, ugyanazzal a frekvenciával. Az amplitudóra az összegzés eredménye:
és a fázisszögre:
Ezek a formulák tetszőleges számú, azonos frekvenciájú harmonikus rezgés összeadására általánosíthatóak.
Két eltérő frekvenciájú, de azonos amplitudójú és fázisú rezgés összetételének eredménye pedig:
Az eredő amplitudó pedig:
Az eredő amplitudó időbeli harmonikus változása a lebegés jelensége.
Csatolt rezgések
Csatolt rezgésről akkor beszélünk, hogyha a testeket nem csak az egyensúlyihelyzetükhöz, hanem egymáshoz is harmonikus erő köti. A mozgásegyenletek ekkor:
Megfelelő változócserével a csatolás kitranszformálható, és két független harmonikus rezgőmozgást kapunk eredményül. Ezek összege és különbsége adja a helyfüggvényeket. Az itt megjelenő frekvenciákat normálfrekvenciáknak nevezzük. Ha megvizsgáljuk az energiaviszonyokat, akkor azt tapasztaljuk, hogy a két test harmonikus energiáján (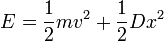 ) kívül fellép egy csatolási energia is:
) kívül fellép egy csatolási energia is:
A teljes energiamegmaradás ennek a három energiának az összegére érvényes. Az időfejlődés során periodikusan változik az egyik és a másik test rezgési amplitudója, szemléletesen az energia oda-vissza vándorol a két test között.
Lineáris lánc
Tekintsünk egy N tömepontból álló sorozatot, amelyet ideális rugók kötnek össze. Tekintsünk el a külső erőtértől. Ekkor az egyes mozgásegyenletek a következő alakúak:
Osszunk át a tömegek négyzetgyökével és vezessük be a következő jelölést: 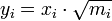 . Az egyszerűség kedvéért, csak szemléltetésül az egyik középső egyenlet így alakul:
. Az egyszerűség kedvéért, csak szemléltetésül az egyik középső egyenlet így alakul:
Az így kapott egyenletrendszer sokkal áttekinthetőbb, ha mátrixos alakba írjuk.
Az itt bevezetett M mátrix tartalmazza a tömegekből, és rugóállandókból adódó konstansokat. A fenti változócserére azért volt szükség, hogy ez a mátrix szimmetrikus legyen, így a sajátértékei valósak. Ez pedig azért jó, mert ekkor a sajátértékprobléma megoldásával megkapott sajátértékek a normálfrekvenciák négyzeteit adják, a sajátvektorok pedig a rezgési módusokat (azaz, hogy az egyes pontok mekkora amplitúdóval, milyen irányba rezegnek). A mátrixnak mindig lesz egy 0 sajátértéke, ez a transzlációt írja le. Az általános megoldás most is az egyes meghatározott frekvenciák és amplitúdók által definiált harmonikus rezgőmozgások eredője, amiben a szabad paramétereket (összesen 2N darab) a kezdőfeltételek szabják meg.
A Kepler-probléma
A Kepler-probléma a Newtoni-gravitációs erőtörvény hatására mozgó test mozgásegyenletének vizsgálata. Ez tulajdonképpen egy centrális erőtérben történő mozgás, azonban kitüntetett jelentősége volt a csillagászat fejlődésében, hiszen jó közelítéssel írja le a Bolygók mozgását a Nap körül.
A bolygók mozgása
Adott a Newton-i gravitációs erőtörvény, itt most vektoros alakban felírva:
itt m az adott bolygó, M a Nap tömege. Ez az erő centrális, azaz a tekintett testek középpontján keresztül hat. Ebből következik, hogy a mozgás síkmozgás, amihez tartozik egy megmaradó mennyiség, az impulzusmomentum:
A mozgásegyenleteket polárkoordinátákban felírva a gyorsulás radiális egyenlete:
És a síkszöghöz tartozó egyenlet:
hiszen az erőnek nincs ilyen irányú komponense. Ezt az egyenletet az impulzusmomentum állandósága megoldja, tehát csak az első egyenlet megoldása marad hátra. Ennek érdekében az idő szerinti deriváltakat átírjuk szögszerinti deriváltakra, azaz áttértünk a szögre, mint paraméterre. Az eredményül kapható differenciál-egyenlet:
ami nem más, mint egy harmonikus oszcillátor egyenlete. Ennek ismert a megoldása, amelyből a sugár kifejezhető:
A koszinuszos tag szorzófaktora az ekcentricitás, a külső tört szorzófaktora a pálya paramétere. A kapott egyenlet egy kúpszelet egyenlete.
A Kepler-mozgások és a kúpszeletek kapcsolata
Az előzőekben bemutattuk, hogy a Kepler-probléma kúpszelet egyenletre vezet, amelyek általános alakja:
Ekkor három alapvetően különböző mozgás jöhet létre, amelyeket az excentricitás különböztet meg:
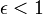 : Ellipszis (speciálisan, 0 esetén kör),
: Ellipszis (speciálisan, 0 esetén kör),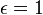 : Parabola,
: Parabola,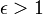 : Hiperbola.
: Hiperbola.
Ezek kifejezhetőek az energiával is:
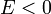 : Ellipszis,
: Ellipszis,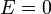 : Parabola,
: Parabola,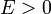 : Hiperbola.
: Hiperbola.
Kozmikus sebességek
A fenti energiák fontosak az űrkutatásban. Ha a Földről indítunk egy testet, akkor a legkisebb energiájú stabil pálya a valamely ellipszis pálya elérése. Első kozmikus sebességnek nevezzük a föld sugarával egyező körpálya eléréséhez szükséges sebességet, ez kb. 7,9 km/s. A második kozmikus sebesség a Föld gravitációs terének elhagyása, azaz a fenti esetek közül a parabolikushoz tartozó sebesség, ez kb.: 11,2 km/s. A harmadik kozmikus sebesség az előző, de a Napra viszonyítva, azaz ebben az esetben a naprendszer elhagyásáról beszélünk. Ez megközelítőleg 42,1 km/s.
Kvantummechanikai problémák
Potenciálvölgy
Oszcillátor Sommerfeld-módszerrel
A lineáris harmonikus oszcillátor energia operátora:
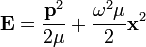 .
.
Az 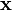 operátor helyére az x szerinti szorzást, a
operátor helyére az x szerinti szorzást, a 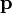 helyére pedig a
helyére pedig a 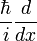 -t írva a sajátérték-egyenlet:
-t írva a sajátérték-egyenlet:
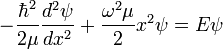 , ebből:
, ebből:
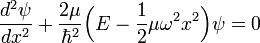 .
.
Bevezetve a 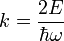 jelölést és x-ről áttérve a
jelölést és x-ről áttérve a 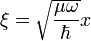 változóra az egyenlet a következőképpen néz ki:
változóra az egyenlet a következőképpen néz ki:
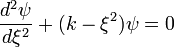 .
.
Az egyenlet aszimptotikus alakja: 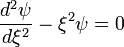 . Ennek megoldása:
. Ennek megoldása: 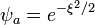 . Az eredeti egyenlet megoldását a Sommerfeld-féle polinom-módszer segítségével szeretnénk megkapni, ezért a pontos megoldást
. Az eredeti egyenlet megoldását a Sommerfeld-féle polinom-módszer segítségével szeretnénk megkapni, ezért a pontos megoldást 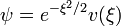 alakban keressük. Ezt beírva a differenciálegyenletbe kapjuk:
alakban keressük. Ezt beírva a differenciálegyenletbe kapjuk:
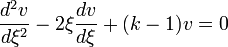 .
.
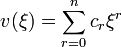 alakban felírva képezzük
alakban felírva képezzük 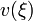 első és második deriváltját:
első és második deriváltját:
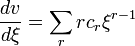 ,
,
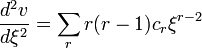 .
.
Ezt beírva 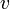 differenciálegyenletébe:
differenciálegyenletébe: 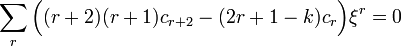 .
.
Ez akkor igaz, ha 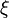 minden hatványának együthatója 0. Így egy rekurzív összefüggést kapunk a
minden hatványának együthatója 0. Így egy rekurzív összefüggést kapunk a 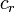 együtthatók között:
együtthatók között:
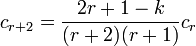 .
.
Belátható, hogy r = n fokszámtól kezdve az összes együtthatónak azonosan 0-nak kell lennie, ezért 2n + 1 = k. Az E és k közötti összefüggés alapján így az energia sajátértékek:
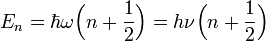 .
.
Az egyes energia sajátértékekhez tartozó sajátfüggvények: 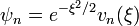 , ahol
, ahol 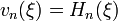 ún. Hermite-polinom.
ún. Hermite-polinom.
Oszcillátor léptető operátorokkal
A harmonikus oszcillátor Hamilton-operátora némi alakítgatás után:
A léptetőoperátorok:
ezek természetesen egymás adjungáltjai. A felcserélési reláció:
Legyen 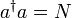 a részecskeszám-operátor. Koncentráljunk ennek a sajátállapotaira:
a részecskeszám-operátor. Koncentráljunk ennek a sajátállapotaira:
Könnyen megmutatható, hogy ha 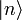 sajátállapota N-nek, akkor
sajátállapota N-nek, akkor 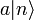 és
és 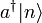 is:
is:
az így kapott sajátállapotok nem normáltak. Mivel 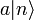 normája n, ezért a normált állapotok:
normája n, ezért a normált állapotok:
és hasonlóan:
Tehát elindulva egy n sajátérékről, az a eltüntető operátor n-1,n-2,... sajátértékkel generál új N sajátállapotokat. Ezek sorozata viszont nem mehet negatívba, hiszen az N sajátérétke egyben a :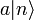 normája ami nem negatív. Ez csak úgy lehet, ha n egész értékéről indulunk, majd elérünk n=0-hoz és akkor:
normája ami nem negatív. Ez csak úgy lehet, ha n egész értékéről indulunk, majd elérünk n=0-hoz és akkor:
Ebből az egyenletből rögtön adódik az alapállapoti hullámfüggvény, a keltő operátor alkalmazással pedig a gerjesztett állapotok hullámfüggvényei. A spektrum is azonnal leolvasható.
Rotátor
A forgó mozgást végző tömegpontot rotátornak nevezzük. Szabadon forgó tömegpont energia sajátérték egyenlete: 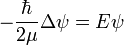 . A problémához leginkább a térbeli polárkoordináta-rendszer illeszkedik, ugyanis a forgás centrumától mért r távolság állandó.
. A problémához leginkább a térbeli polárkoordináta-rendszer illeszkedik, ugyanis a forgás centrumától mért r távolság állandó.
A Laplace-operátor polárkoordináta rendszerben: 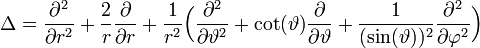 .
.
r = állandó, ezért 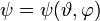 csak a szögektől függ:
csak a szögektől függ:
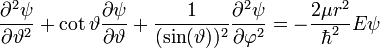 .
.
Legyen 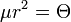 (a tehetetlenségi nyomaték a forgás centrumára vonatkozóan). Az egyenlet a következő alakra módosul:
(a tehetetlenségi nyomaték a forgás centrumára vonatkozóan). Az egyenlet a következő alakra módosul:
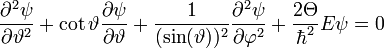 .
.
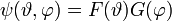 alakban keresve a megoldást:
alakban keresve a megoldást:
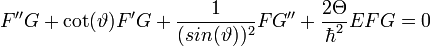 .
.
Átalakítva: 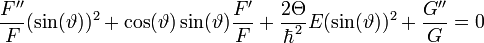 .
.
A 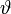 -tól és a
-tól és a 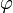 -től függő részek külön-külön állandók kell, hogy legyenek:
-től függő részek külön-külön állandók kell, hogy legyenek:
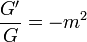 , azaz
, azaz 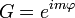 .
.
Az azimutszöget 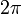 -vel növelve ugyanabba a pontba jutunk vissza, ezért meg kell követelnünk, hogy
-vel növelve ugyanabba a pontba jutunk vissza, ezért meg kell követelnünk, hogy 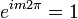 legyen.
legyen.
Az F-et meghatározó egyenletnél érdemes a 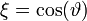 változóra áttérni, így az eredeti egyenletet
változóra áttérni, így az eredeti egyenletet 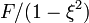 -tel megszorozva (
-tel megszorozva (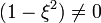 ) kapjuk:
) kapjuk:
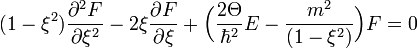 .
.
A 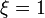 -ben a differenciálegyenletnek szingularitása van, hogy a megoldás itt is véges legyen, ezért
-ben a differenciálegyenletnek szingularitása van, hogy a megoldás itt is véges legyen, ezért 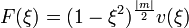 . Ezt visszaírva és a kapott egyenlet megoldását a polinom-módszer alapján
. Ezt visszaírva és a kapott egyenlet megoldását a polinom-módszer alapján 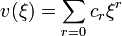 alakban keresve kapjuk:
alakban keresve kapjuk:
![\sum_{r} \left((r+2)(r+1) c_{r+2} - \Bigl[ (r+|m|)(r+|m|+1)- \frac{2 \Theta E}{\hbar^{2}} \Bigr] c_{r} \right) \xi^{r} = 0](/images/math/d/9/0/d90cc3e9c3bea5f9ab19616bc5d070e9.png) .
.
Ez alapján a 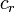 együtthatókra egy rekurziós képletet kapunk:
együtthatókra egy rekurziós képletet kapunk: 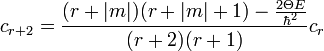 .
.
Ahhoz, hogy a sajátfüggvény reguláris legyen egy bizonyos fokszámú együtthatótól kezdve az összes értéke azonosan 0 kell hogy legyen. A lehetséges energia-sajátértékek így: 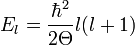 , ahol
, ahol 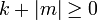 -t jelöltük l-el (l = 0, 1, 2, ...).
-t jelöltük l-el (l = 0, 1, 2, ...).
A differenciálegyenletet kielégítő polinom neve módosított Legendre-polinom, amit 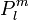 szimbólummal jelölünk. A forgó mozgást végző tömegpont sajátfüggvényei tehát a gömbfüggvények:
szimbólummal jelölünk. A forgó mozgást végző tömegpont sajátfüggvényei tehát a gömbfüggvények:
![\psi_{lm}(\vartheta, \varphi) = Y_{lm}(\vartheta, \varphi) = \sqrt{\frac{2l+1}{4 \pi}\frac{(l-m)!}{(l+m)!}}P_{l}^{m}[\cos(\vartheta)]e^{i m \varphi}](/images/math/5/1/5/5158669d00173bd328c7b752459882b4.png) .
.
A teljes energia: 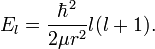
Az impulzusmomentum négyzete: 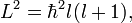 a
a 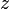 irányú vetülete pedig
irányú vetülete pedig 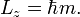
A Schrödinger-egyenlet megoldása Coulomb-potenciálban, H-atom
A szögfüggő tagok leválasztása után:
Bevezetve 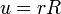 -t:
-t:
Ezek után dimenziótlanítunk. Legyen 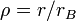 és
és 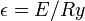 , ahol a Bohr-sugár
, ahol a Bohr-sugár 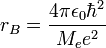 és a Rydberg-állandó
és a Rydberg-állandó 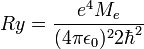 . Ekkor:
. Ekkor:
A szükséges határfeltételek:
-
 -ben u=0.
-ben u=0.
-
 -ban?
-ban?
Ha 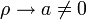 akkor
akkor 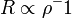 , erre hattatva a Laplace operátort az origóban Dirac-deltát kapunk, vagyis nem elégítjük ki a Schrödinger-egyenletet. Ezért itt is u=0 lesz a határfeltétel.
, erre hattatva a Laplace operátort az origóban Dirac-deltát kapunk, vagyis nem elégítjük ki a Schrödinger-egyenletet. Ezért itt is u=0 lesz a határfeltétel.
Az egyenlet megoldási módszere Sommerfeld féle polinom módszer:
- Megoldjuk az egyenletet aszimptotikusan.
Az aszimptotikus megoldás 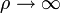 -ben
-ben 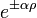 ahol
ahol 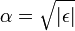 . A norma miatt csak a negatív előjel jó.
. A norma miatt csak a negatív előjel jó.
- A megoldást
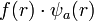 alakban keressük, ahol
alakban keressük, ahol 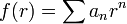 hatványsor. Az f(r) eredeti egyenletbe való visszahelyettesítése után kapunk egy rekurziót az
hatványsor. Az f(r) eredeti egyenletbe való visszahelyettesítése után kapunk egy rekurziót az 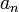 -ekre.
-ekre. - A rekurzió megoldása elrontja az aszimptotikát, az egyetlen megoldás, ha a hatványsorunk véges, vagyis valamilyen n-re
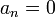 . Ebből a feltételből közvetlenül kapjuk az energiaszinteket. Az együtthatók kiszámolásával pedig a sajátfüggvényeket.
. Ebből a feltételből közvetlenül kapjuk az energiaszinteket. Az együtthatók kiszámolásával pedig a sajátfüggvényeket.
Az energiaszintek:
Minden energiaszint 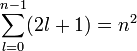 -szeresen degenerált.
-szeresen degenerált.
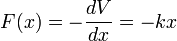
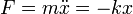
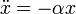
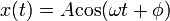
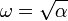
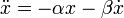
![x(t) = \operatorname{exp}\left[ \frac{1}{2}\left(-\beta \pm \sqrt{\beta^2 - 4\alpha} \right)t\right],](/images/math/f/f/3/ff3427e5232dbc2f33f4c92421734136.png)
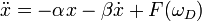
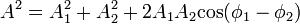
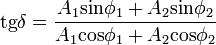
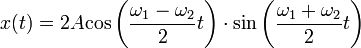
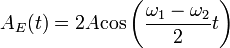
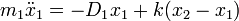
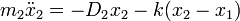
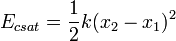
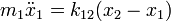
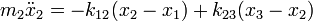
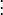
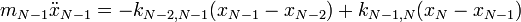
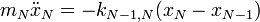
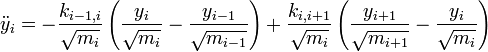
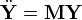
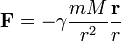
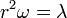
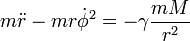
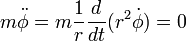
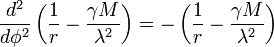
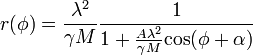
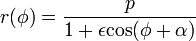
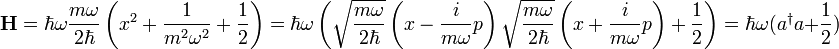
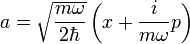
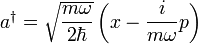
![[a,a^\dagger]=1\,](/images/math/c/a/2/ca294b5fddde3b091c8a4ccbf89992b1.png)